Fonction bêta
En mathématiques, la fonction bêta est une des deux intégrales d'Euler , définie pour tous nombres complexes x et y de parties réelles strictement positives par :
B
(
x
,
y
)
=
∫
0
1
t
x
−
1
(
1
−
t
)
y
−
1
d
t
,
{\displaystyle \mathrm {B} (x,y)=\int _{0}^{1}t^{x-1}(1-t)^{y-1}\mathrm {d} t,}
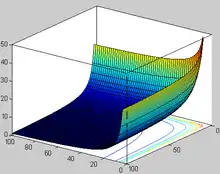
Variations de la fonction bêta pour les valeurs positives de x et y
et éventuellement prolongée analytiquement à tout le plan complexe à l'exception des entiers négatifs.
La fonction bêta a été étudiée par Euler et Legendre et doit son nom à Jacques Binet . Elle est en relation avec la fonction gamma .
Il existe aussi une version incomplète de la fonction bêta, la fonction bêta incomplète ainsi qu'une version régularisée de celle-ci, la fonction bêta incomplète régularisée .
Propriétés Dans sa définition sous forme d'intégrale, le changement de variable u = 1 – t symétrique c'est-à-dire que :
B
(
x
,
y
)
=
B
(
y
,
x
)
{\displaystyle \mathrm {B} (x,y)=\mathrm {B} (y,x)}
Elle peut prendre aussi les formes intégrales
B
(
x
,
y
)
=
2
∫
0
π
/
2
sin
2
x
−
1
θ
cos
2
y
−
1
θ
d
θ
{\displaystyle \mathrm {B} (x,y)=2\int _{0}^{\pi /2}\sin ^{2x-1}\theta ~\cos ^{2y-1}\theta ~\mathrm {d} \theta }
t
=
sin
2
θ
{\displaystyle t=\sin ^{2}\theta }
B
(
x
,
y
)
=
∫
0
∞
s
y
−
1
(
1
+
s
)
x
+
y
d
s
{\displaystyle \mathrm {B} (x,y)=\int _{0}^{\infty }{\frac {s^{y-1}}{(1+s)^{x+y}}}~\mathrm {d} s}
t
=
1
1
+
s
{\displaystyle t={\dfrac {1}{1+s}}}
Elle satisfait des équations fonctionnelles telles que :
B
(
x
,
y
+
1
)
=
y
x
+
y
B
(
x
,
y
)
{\displaystyle \mathrm {B} (x,y+1)={y \over x+y}\mathrm {B} (x,y)}
B
(
x
,
y
)
B
(
x
+
y
,
1
−
y
)
=
π
x
sin
(
π
y
)
{\displaystyle \mathrm {B} (x,y)~\mathrm {B} (x+y,1-y)={\dfrac {\pi }{x\sin(\pi y)}}}
B
(
x
,
x
)
=
2
1
−
2
x
B
(
1
2
,
x
)
{\displaystyle \mathrm {B} (x,x)=2^{1-2x}\mathrm {B} \left({\tfrac {1}{2}},x\right)}
Elle est liée à la fonction gamma par l'équation suivante[1]
B
(
x
,
y
)
=
Γ
(
x
)
Γ
(
y
)
Γ
(
x
+
y
)
{\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\,\Gamma (y)}{\Gamma (x+y)}}}
Si x et y sont des entiers strictement positifs, cette équation se réécrit, en termes de factorielles ou de coefficient binomial :
x
+
y
x
y
B
(
x
,
y
)
=
(
x
+
y
)
!
x
!
y
!
=
(
x
+
y
x
)
{\displaystyle {\frac {x+y}{xy\mathrm {B} (x,y)}}={\frac {(x+y)!}{x!~y!}}={x+y \choose x}}
Si x et y sont deux rationnels et si ni x , ni y , ni x + y Β(x , y ) est un nombre transcendant [2]
Dérivation Les dérivées partielles de la fonction bêta utilisent les équations fonctionnelles vues précédemment :
∂
∂
x
B
(
x
,
y
)
=
B
(
x
,
y
)
(
Γ
′
(
x
)
Γ
(
x
)
−
Γ
′
(
x
+
y
)
Γ
(
x
+
y
)
)
=
B
(
x
,
y
)
(
ψ
(
x
)
−
ψ
(
x
+
y
)
)
,
{\displaystyle {\partial \over \partial x}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left({\Gamma '(x) \over \Gamma (x)}-{\Gamma '(x+y) \over \Gamma (x+y)}\right)=\mathrm {B} (x,y)(\psi (x)-\psi (x+y)),}
où ψ (x )fonction digamma .
∂
2
∂
x
2
B
(
x
,
y
)
=
B
(
x
,
y
)
[
(
ψ
(
x
)
−
ψ
(
x
+
y
)
)
2
+
(
ψ
1
(
x
)
−
ψ
1
(
x
+
y
)
)
]
,
{\displaystyle {\partial ^{2} \over \partial x^{2}}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left[(\psi (x)-\psi (x+y))^{2}+(\psi _{1}(x)-\psi _{1}(x+y))\right],}
∂
2
∂
x
∂
y
B
(
x
,
y
)
=
B
(
x
,
y
)
[
(
ψ
(
x
)
−
ψ
(
x
+
y
)
)
(
ψ
(
y
)
−
ψ
(
x
+
y
)
)
−
ψ
1
(
x
+
y
)
]
,
{\displaystyle {\partial ^{2} \over {\partial x\partial y}}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left[(\psi (x)-\psi (x+y))(\psi (y)-\psi (x+y))-\psi _{1}(x+y)\right],}
où ψn (x )fonction polygamma .
Fonction bêta incomplète La fonction bêta incomplète est définie par :
B
(
x
;
a
,
b
)
=
∫
0
x
t
a
−
1
(
1
−
t
)
b
−
1
d
t
{\displaystyle \mathrm {B} (x;\,a,b)=\int _{0}^{x}t^{a-1}\,(1-t)^{b-1}\mathrm {d} t}
et vérifie trivialement [3]
B
(
x
;
a
+
1
,
b
)
+
B
(
x
;
a
,
b
+
1
)
=
B
(
x
;
a
,
b
)
e
t
x
a
(
1
−
x
)
b
=
a
B
(
x
;
a
,
b
+
1
)
−
b
B
(
x
;
a
+
1
,
b
)
.
{\displaystyle \mathrm {B} (x;\,a+1,b)+\mathrm {B} (x;\,a,b+1)=\mathrm {B} (x;\,a,b)\quad {\rm {et}}\quad x^{a}(1-x)^{b}=a\mathrm {B} (x;\,a,b+1)-b\mathrm {B} (x;\,a+1,b).}
Pour x = 1a et b .
La fonction bêta incomplète régularisée consiste à diviser la fonction bêta incomplète par la fonction bêta complète
I
x
(
a
,
b
)
=
B
(
x
;
a
,
b
)
B
(
a
,
b
)
.
{\displaystyle I_{x}(a,b)={\dfrac {\mathrm {B} (x;\,a,b)}{\mathrm {B} (a,b)}}.}
Les relations précédentes deviennent ainsi
a
I
x
(
a
+
1
,
b
)
+
b
I
x
(
a
,
b
+
1
)
=
(
a
+
b
)
I
x
(
a
,
b
)
{\displaystyle aI_{x}(a+1,b)+bI_{x}(a,b+1)=(a+b)I_{x}(a,b)}
[4]
,
I
x
(
a
,
b
+
1
)
−
I
x
(
a
+
1
,
b
)
=
x
a
(
1
−
x
)
b
a
+
b
a
b
B
(
a
,
b
)
.
{\displaystyle ,\quad I_{x}(a,b+1)-I_{x}(a+1,b)=x^{a}(1-x)^{b}{\frac {a+b}{ab\mathrm {B} (a,b)}}.}
On déduit de la seconde (par une récurrence immédiate) le lien suivant avec le développement binomial et la loi binomiale [4]
I
p
(
a
,
n
−
a
+
1
)
=
∑
j
=
a
n
(
n
j
)
p
j
(
1
−
p
)
n
−
j
.
{\displaystyle I_{p}(a,n-a+1)=\sum _{j=a}^{n}{n \choose j}p^{j}(1-p)^{n-j}.}
Notes et références Pour une démonstration, voir par exemple cet exercice corrigé . (de) Theodor Schneider , « Zur Theorie der Abelschen Funktionen und Integrale » , J. reine angew. Math. vol. 183, 1941 , p. 110-128 (lire en ligne ) (en) M. Aslam Chaudhry et Syed M. Zubair , On a Class of Incomplete Gamma Functions with Applications , CRC Press , 2001 (ISBN 978-1-58488-143-8 , lire en ligne ) , p. 218 (en) Milton Abramowitz et Irene Stegun , Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables[ détail de l’édition] (lire en ligne )
Lien externe (en) Eric W. Weisstein , « Beta Function MathWorld
Cet article est issu de
wikipedia . Text licence:
CC BY-SA 4.0 , Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.












![{\displaystyle {\partial ^{2} \over \partial x^{2}}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left[(\psi (x)-\psi (x+y))^{2}+(\psi _{1}(x)-\psi _{1}(x+y))\right],}](https://img.franco.wiki/i/269f4d6846c681f1de9a67e72c5c86027dac6b36.svg)
![{\displaystyle {\partial ^{2} \over {\partial x\partial y}}\mathrm {B} (x,y)=\mathrm {B} (x,y)\left[(\psi (x)-\psi (x+y))(\psi (y)-\psi (x+y))-\psi _{1}(x+y)\right],}](https://img.franco.wiki/i/5983465f645fb43e82d815bee1e87002a948afe3.svg)





