Fonction gamma

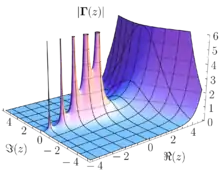
En mathématiques, la fonction gamma (notée par la lettre grecque $Γ$ ) est une fonction complexe, considérée également comme une fonction spéciale. Elle prolonge la fonction factorielle à l'ensemble des nombres complexes (à l'exception des entiers négatifs). On a : $\forall n>0,\Gamma (n)=(n-1)!=1\times 2\times \dots \times (n-1)$

Tracé de la fonction gamma le long de l'axe des réels.

Définition

Tracé du module de la fonction gamma dans le plan complexe.

Pour tout nombre complexe z tel que Re(z) > 0, on définit la fonction suivante, appelée fonction gamma, et notée par la lettre grecque $Γ$ (gamma majuscule)

\Gamma :z\mapsto \int _{0}^{+\infty }t^{z-1}\,\mathrm {e} ^{-t}\,\mathrm {d} t

Cette intégrale impropre converge absolument sur le demi-plan complexe où la partie réelle est strictement positive[1], et une intégration par parties[1] montre que

\Gamma (z+1)=z\;\Gamma (z)

Cette fonction peut être prolongée analytiquement en une fonction méromorphe sur l'ensemble des nombres complexes, excepté pour z = 0, −1, −2, −3… qui sont des pôles. C'est ce prolongement qu'on appelle généralement « fonction gamma ». L'unicité du prolongement analytique permet de montrer que la fonction prolongée vérifie encore l'équation fonctionnelle précédente. Cela permet une définition plus simple, à partir de l'intégrale, et un calcul de proche en proche de Γ pour z – 1, z – 2, etc.

Autres définitions

Par changement de variable, l'intégrale précédente (pour $Re(z) > 0$ ) s'écrit aussi :

\Gamma (z)=2\int _{0}^{+\infty }u^{2z-1}\mathrm {e} ^{-u^{2}}\,\mathrm {d} u\quad {\text{et}}\quad \Gamma (z)=\int _{0}^{1}\left(-\ln s\right)^{z-1}\,\mathrm {d} s

La définition suivante de la fonction gamma par produits infinis, due à Euler, a un sens pour les nombres complexes $z$ qui ne sont pas des entiers négatifs ou nuls[2] :

\Gamma (z)=\lim _{n\to {+\infty }}{\frac {n!\;n^{z}}{z\;(z+1)\cdots (z+n)}}={\frac {1}{z}}\,\prod _{k=1}^{+\infty }{\frac {\left(1+1/k\right)^{z}}{1+z/k}}

Elle est équivalente à celle donnée par Schlömilch[3] - [4] - [5] :

\Gamma (z)={\frac {\operatorname {e} ^{-\gamma z}}{z}}\prod _{k=1}^{+\infty }{\frac {\operatorname {e} ^{z/k}}{1+z/k}}

où $\gamma =\sum _{k=1}^{\infty }\left[{\frac {1}{k}}-\ln \left(1+{\frac {1}{k}}\right)\right]$ est la constante d'Euler-Mascheroni.

Propriétés

Lien avec la factorielle

De $Γ(z +1) = z Γ (z)$ et $Γ(1) = 1$ , on déduit :

\forall \,n\in \mathbb {N} ,\;\Gamma (n+1)=n!

On interprète donc la fonction gamma comme un prolongement de la factorielle à l'ensemble des nombres complexes (à l'exception des entiers négatifs ou nuls).

Une notation alternative est la fonction $Π$ , introduite par Gauss :

\Pi (z)=\Gamma (z+1)=z\;\Gamma (z)

(et donc

\Gamma (z)=\Pi (z-1)=\Pi (z)/z

de telle façon que :

\Pi (n)=n!

Sur l'ensemble des réels

La fonction gamma est entièrement caractérisée sur $\mathbb {R} _{+}^{*}$ par les trois propriétés suivantes (théorème de Bohr-Mollerup) :

$\Gamma (1)=1\,$
Pour tout $x>0\,$ , on a : $\Gamma (x+1)=x\;\Gamma (x)\,$
la fonction composée $\ln \circ \,\Gamma$ est convexe sur $\mathbb {R} _{+}^{*}$

Sur le demi-plan complexe Re(z)>0

La fonction gamma est entièrement caractérisée parmi les fonctions holomorphes du demi-plan complexe Re(z)>0 par les trois propriétés suivantes (théorème de Wielandt) :

$\Gamma (1)=1\,$
Pour tout z tel que $Re(z) > 0$ , $\Gamma (z+1)=z\;\Gamma (z)\,$
$|\Gamma (z)|\,$ est bornée dans la bande 1 ≤ Re(z) ≤ 2.

Autres propriétés

Formule des compléments

La fonction gamma vérifie la formule de réflexion d'Euler, ou formule des compléments

\forall z\in \mathbb {C} \setminus \mathbb {Z} \quad \Gamma (1-z)\;\Gamma (z)={\pi  \over \sin(\pi z)},

que l'on démontre en remarquant d'abord que $Γ(1 - z)Γ(z)$ est 2-périodique et a les mêmes pôles et résidus que ${\tfrac {\pi }{\sin(\pi z)}}$ .

Formule de multiplication

La fonction gamma vérifie également la formule de duplication : $\Gamma (z)\;\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z).$

La formule de duplication est un cas particulier du théorème de multiplication :

\Gamma (z)\;\Gamma \left(z+{\frac {1}{m}}\right)\;\Gamma \left(z+{\frac {2}{m}}\right)\cdots \Gamma \left(z+{\frac {m-1}{m}}\right)=(2\pi )^{(m-1)/2}\;m^{1/2-mz}\;\Gamma (mz).

Cette fonction apparaît également dans des formules incluant la fonction zêta de Riemann.

Résidus

La fonction gamma possède un pôle d'ordre 1 en z = −n pour tout entier naturel n. Le résidu de la fonction en ce pôle est donné par :

\operatorname {Res} (\Gamma ,-n)={\frac {(-1)^{n}}{n!}}.

Dérivées

La fonction gamma est infiniment dérivable sur $\mathbb {R} _{+}^{*}$ (c’est-à-dire p fois dérivable pour tout entier p). Sa dérivée est exprimée à l'aide de la fonction digamma : $\Gamma '(z)=\Gamma (z)\psi _{0}(z).\,$

Plus généralement, sa dérivée p-ième possède sur $\mathbb {R} _{+}^{*}$ l'expression intégrale suivante :

\Gamma ^{(p)}(x)=\int _{0}^{+\infty }{(\ln t)^{p}\,t^{x-1}\,\operatorname {e} ^{-t}\,\mathrm {d} t}

Lien avec les sommes de Gauss

La définition de la fonction gamma sous forme d'intégrale la fait apparaître comme une convolution entre un caractère additif (l'exponentielle) et un caractère multiplicatif ( $x\mapsto x^{s}$ ).

Lien avec d'autres fonctions

La fonction gamma est reliée à la fonction $ζ$ de Riemann par :

\zeta (s)\,\Gamma (s)=\int _{0}^{+\infty }{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\,\mathrm {d} t

Elle est reliée à la fonction êta de Dirichlet par :

\Gamma (s)\,\eta (s)=\int _{0}^{\infty }{\frac {x^{s-1}}{\mathrm {e} ^{x}+1}}\,\mathrm {d} x

=[6]

\int _{0}^{1}\int _{0}^{1}{\frac {(-\ln(xy))^{s-2}}{1+xy}}\,\mathrm {d} x\,\mathrm {d} y

Dans la définition de la fonction gamma sous forme d'intégrale, les bornes de l'intégrale sont fixées ; la fonction gamma incomplète est la fonction obtenue en modifiant la borne inférieure ou la borne supérieure.

La fonction gamma est reliée à la fonction bêta par la formule :

\mathrm {B} (x,y)={\frac {\Gamma (x)\;\Gamma (y)}{\Gamma (x+y)}}.

Le logarithme de la fonction gamma est parfois appelé lngamma. Il intervient notamment dans la résolution des problèmes de propagation d’ondes[7] : l'équation fonctionnelle de la fonction lngamma est :

\ln \Gamma (z)=\ln \Gamma (z+1)-\ln(z)

Si l’on connaît les valeurs de la fonction sur une bande de largeur 1 en Re(z), on obtient par cette relation les valeurs dans une bande voisine de même largeur, et l’on peut répéter ce procédé. Partant d’un z avec Re(z) >> 1 pour lequel on connaît une bonne approximation, on peut ainsi atteindre la valeur pour un z quelconque.

Rocktaeschel (1922[8], suivant une indication de Gauss) propose l'approximation pour $Re(z)$ grand :

\ln \Gamma (z)\approx (z-{\tfrac {1}{2}})\ln z-z+{\tfrac {1}{2}}\ln(2\pi )

On peut en déduire une approximation de $ln Γ(z)$ pour $Re(z)$ plus petit, en utilisant[9] :

\ln \Gamma (z-m)=\ln \Gamma (z)-\sum _{k=1}^{m}\ln(z-k)

La dérivée logarithmique de la fonction gamma est appelée fonction digamma. Les dérivées d'ordre supérieur sont les fonctions polygamma.

Un analogue de la fonction gamma sur un corps fini ou un anneau fini est fourni par les sommes de Gauss.

D'après l'expression d'Euler pour la fonction gamma (voir supra), son inverse (en) $g(z)={\frac {1}{\Gamma (z)}}$ est une fonction entière.

Valeurs particulières

Cette section indique quelques valeurs particulières de la fonction gamma (en) et de ses dérivées.

La valeur de $Γ(1/2) = \sqrt π$ est celle de l'intégrale de Gauss ; elle peut aussi se déduire de la formule des compléments. Cette valeur permet, par récurrence, de déterminer les autres valeurs de la fonction gamma pour les demi-entiers positifs :

\Gamma (3/2)={\frac {\sqrt {\pi }}{2}},\quad \Gamma (5/2)={\frac {3{\sqrt {\pi }}}{4}},\ldots ,

\Gamma \left(n+{\frac {1}{2}}\right)=\left(n-{\frac {1}{2}}\right)\Gamma \left(n-{\frac {1}{2}}\right)=\left(n-{\frac {1}{2}}\right)\left(n-{\frac {3}{2}}\right)\cdots {\frac {3}{2}}\,{\frac {1}{2}}\,\Gamma \left({\frac {1}{2}}\right)={\frac {(2n)!}{2^{2n}n!}}{\sqrt {\pi }}

mais aussi négatifs, par exemple :

\Gamma (-1/2)=-2{\sqrt {\pi }}

En ce qui concerne ses dérivées, avec $γ$ la constante d'Euler-Mascheroni :

\Gamma '(n+1)=\Gamma (n+1)\psi _{0}(n+1)=n!\left(-\gamma +\sum _{1\leq k\leq n}{\frac {1}{k}}\right)

;

\Gamma '\left(n+{\frac {1}{2}}\right)=\Gamma \left(n+{\frac {1}{2}}\right)\psi _{0}\left(n+{\frac {1}{2}}\right)={\frac {(2n)!}{2^{2n}n!}}{\sqrt {\pi }}\left(-\gamma -2\ln 2+\sum _{1\leq k\leq n}{\frac {2}{2k-1}}\right)

;

\Gamma ''(1/2)={\sqrt {\pi }}(\gamma +2\,\ln(2))^{2}+{\frac {\pi ^{5/2}}{2}},\quad \Gamma ''(1)=\gamma ^{2}+{\frac {\pi ^{2}}{6}},\quad \Gamma ''(2)=(1-\gamma )^{2}+{\frac {\pi ^{2}}{6}}-1

On connaît quelques résultats de transcendance et même d'indépendance algébrique sur les valeurs de $Γ$ en certains points rationnels.

Une conjecture de Rohrlich[10] prédit que toute relation multiplicative de la forme

\pi ^{b/2}\prod \Gamma (a_{k})^{m_{k}}\in {\overline {\mathbb {Q} }},\quad (b\in \mathbb {Z} ,\;a_{k}\in \mathbb {Q} ,\;m_{k}\in \mathbb {Z} )

(où ℚ désigne le corps des nombres algébriques) se déduit des trois relations standard :

\Gamma (z+1)=z\Gamma (z),\quad \Gamma (1-z)\Gamma (z)={\pi  \over \sin(\pi z)},\quad \prod _{0\leq k<n}\Gamma \left(z+{\frac {k}{n}}\right)=(2\pi )^{(n-1)/2}n^{-nz+1/2}\Gamma (nz)

Formule asymptotique de Stirling

De $Γ(z)$ et $Γ(z +1)$

La formule de Stirling donne un équivalent au voisinage de l'infini de la factorielle :

n\,!={\sqrt {2\pi }}\,n^{n+{\frac {1}{2}}}{\rm {e}}^{-n+\mu (n)}{\text{ pour }}n\in \mathbb {N} \ ,

avec $μ$ la fonction de Binet :

\mu (z)=\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)z^{2k-1}}}\ ,

et $B i$ les nombres de Bernoulli. Sachant que $Γ(n +1)= n!$ sur $ℕ$ , cet équivalent se généralise à la fonction gamma :

\Gamma (z+1)={\sqrt {2\pi }}\,z^{z+{\frac {1}{2}}}{\rm {e}}^{-z+\mu (z)}{\text{ pour }}z\in \mathbb {C} \setminus \mathbb {Z_{-}^{*}} \ ,

d’où :

\Gamma (z)={\frac {\Gamma (z+1)}{z}}={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}{\rm {e}}^{-z+\mu (z)}{\text{ pour }}z\in \mathbb {C} \setminus \mathbb {Z_{-}} \ .

En calculant les premiers termes de $e μ$ grâce à la formule exponentielleformule exponentielle, on obtient le développement asymptotique :

\Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}{\rm {e}}^{-z}\left[1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-{\frac {139}{51840z^{3}}}-{\frac {571}{2488320z^{4}}}+{\frac {163879}{209018880z^{5}}}+{\mathcal {O}}\left({\frac {1}{z^{6}}}\right)\right]\ .

De $Γ(z + ½)$

L’équivalent en $z +½$ vaut :

\Gamma \left(z+{\frac {1}{2}}\right)={\sqrt {2\pi }}\,z^{z}{\rm {e}}^{-z+\beta (z)}\ ,

avec :

\beta (z)=\sum _{k=1}^{\infty }{\frac {\left({\frac {1}{2^{2k-1}}}-1\right)B_{2k}}{2k(2k-1)z^{2k-1}}}\ ,

d’où le développement asymptotique :

\Gamma \left(z+{\frac {1}{2}}\right)={\sqrt {2\pi }}\,z^{z}{\rm {e}}^{-z}\left[1-{\frac {1}{24z}}+{\frac {1}{1152z^{2}}}+{\frac {1003}{414720z^{3}}}-{\frac {4027}{39813120z^{4}}}-{\frac {5128423}{6688604160z^{5}}}+{\mathcal {O}}\left({\frac {1}{z^{6}}}\right)\right]\ .

Cas général

De manière plus générale, pour $| a | < | z |$ , l’équivalent en $z + a \notin ℤ -$ vaut :

\Gamma (z+a)={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\exp \left(-z-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k(k-1)(-z)^{k-1}}}\right)

où $B k$ sont les polynômes de Bernoulli.

Démonstration

Par généralisation sur les complexes de la formule de Stirling, on sait que, pour $z \notin ℤ -$ :

\Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}\exp \left(-z+\sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)z^{2k-1}}}\right)

Les nombres de Bernoulli de rang impair supérieur ou égal à 3 étant nuls, on peut également écrire, par changement de variable $i = 2 k$ et en introduisant les termes (nuls) de rang impair :

\Gamma (z)={\sqrt {2\pi }}\,z^{z-{\frac {1}{2}}}\exp \left(-z+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)z^{i-1}}}\right)

d’où :

\Gamma (z+a)={\sqrt {2\pi }}\,(z+a)^{z+a-{\frac {1}{2}}}\exp \left(-(z+a)+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)(z+a)^{i-1}}}\right)

$z$ étant non nul, on peut factoriser $z + a$ en $z \times(1+ a / z)$ :

{\begin{aligned}\Gamma (z+a)&={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\left(1+{\tfrac {a}{z}}\right)^{z+a-{\frac {1}{2}}}\exp \left(-z-a+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)z^{i-1}(1+{\frac {a}{z}})^{i-1}}}\right)\\&={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\exp \left(-z+\left(z+a-{\frac {1}{2}}\right)\ln \left(1+{\frac {a}{z}}\right)-a+\sum _{i=2}^{\infty }{\frac {B_{i}}{i(i-1)z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}\right).\end{aligned}}

Ayant posé $| a | < | z |$ , on a $| a / z | < 1$ , ce qui permet de développer d’une part la série de Taylor du logarithme $ln(1 + x)$ (valable pour $| x | < 1$ ) et d’autre part le binôme négatif $(1 + x) - n$ (valable pour $| x | < 1$ et $n \in ℕ *$ ) :

\ln \left(1+{\tfrac {a}{z}}\right)=-\sum _{k=1}^{\infty }{\frac {\left(-{\frac {a}{z}}\right)^{k}}{k}}=-\sum _{k=1}^{\infty }{\frac {(-a)^{k}}{k\,z^{k}}}=-\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}

\left(1+{\tfrac {a}{z}}\right)^{-(i-1)}=\sum _{j=0}^{\infty }{\binom {i+j-2}{j}}\left(-{\frac {a}{z}}\right)^{j}=\sum _{j=0}^{\infty }{\frac {(i+j-2)!\,(-a)^{j}}{(i-2)!\,j!\,z^{j}}}.

On a donc d’une part, par le développement du logarithme :

z\ln \left(1+{\tfrac {a}{z}}\right)=-\sum _{k=1}^{\infty }{\frac {(-a)^{k}}{k\,z^{k-1}}}=a-\sum _{k=2}^{\infty }{\frac {(-a)^{k}}{k\,z^{k-1}}}

et :

a\ln \left(1+{\tfrac {a}{z}}\right)=-a\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}=\sum _{k=2}^{\infty }{\frac {(-a)^{k}}{(k-1)\,z^{k-1}}}

d’où :

{\begin{aligned}\left(z+a-{\tfrac {1}{2}}\right)\ln \left(1+{\tfrac {a}{z}}\right)-a&=a+\sum _{k=2}^{\infty }\left({\frac {1}{k-1}}-{\frac {1}{k}}\right){\frac {(-a)^{k}}{z^{k-1}}}+{\frac {1}{2}}\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}-a\\&=\sum _{k=2}^{\infty }{\frac {(-a)^{k}}{k\,(k-1)\,z^{k-1}}}+{\frac {1}{2}}\sum _{k=2}^{\infty }{\frac {(-a)^{k-1}}{(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}.\end{aligned}}

On a d’autre part, par le développement du binôme négatif, puis en procédant au changement de variable $k = i + j$ :

{\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}=\sum _{j=0}^{\infty }{\frac {B_{i}\,(i+j-2)!\,(-a)^{j}}{i!\,j!\,z^{i-1+j}}}=\sum _{k=i}^{\infty }{\frac {B_{i}\,(k-2)!\,(-a)^{k-i}}{i!\,(k-i)!\,z^{k-1}}}=\sum _{k=i}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}\ .

Puisque ${\tbinom {k}{i}}=0$ pour $k < i$ , et $i$ valant au moins $2$ , on peut étendre la somme ci-dessus pour $k$ allant de $2$ (en deçà, on aurait la forme indéterminée 0/0) à $i - 1$ (somme de $i - 2$ termes, donc au pire une somme vide, valide, si $i = 2$ ) :

{\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}=\sum _{k=2}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}

On rappelle que les polynômes de Bernoulli vérifient :

B_{k}(x)=\sum _{i=0}^{k}{\binom {k}{i}}B_{i}\,x^{k-i}=B_{0}\,x^{k}+k\,B_{1}\,x^{k-1}+\sum _{i=2}^{k}{\binom {k}{i}}B_{i}\,x^{k-i}=x^{k}-{\frac {k}{2}}\,x^{k-1}+\sum _{i=2}^{k}{\binom {k}{i}}B_{i}\,x^{k-i}

ainsi que :

B_{k}(-x)=(-1)^{k}\left[B_{k}(x)+k\,x^{k-1}\right]=(-1)^{k}B_{k}(x)-k\,(-x)^{k-1}

d’où :

{\begin{aligned}\sum _{i=2}^{\infty }{\frac {B_{i}}{i\,(i-1)\,z^{i-1}}}\left(1+{\frac {a}{z}}\right)^{-(i-1)}&=\sum _{k=2}^{\infty }\sum _{i=2}^{\infty }{\binom {k}{i}}{\frac {B_{i}\,(-a)^{k-i}}{k\,(k-1)\,z^{k-1}}}=\sum _{k=2}^{\infty }{\frac {B_{k}(-a)-(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}B_{k}(a)-k\,(-a)^{k-1}-(-a)^{k}+{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=\sum _{k=2}^{\infty }{\frac {(-1)^{k}B_{k}(a)-(-a)^{k}-{\frac {k}{2}}\,(-a)^{k-1}}{k\,(k-1)\,z^{k-1}}}\\&=-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k\,(k-1)\,(-z)^{k-1}}}-\left[\left(z+a-{\tfrac {1}{2}}\right)\ln \left(1+{\tfrac {a}{z}}\right)-a\right].\end{aligned}}

Donc, pour $| a | < | z |$ :

\Gamma (z+a)={\sqrt {2\pi }}\,z^{z+a-{\frac {1}{2}}}\exp \left(-z-\sum _{k=2}^{\infty }{\frac {B_{k}(a)}{k(k-1)(-z)^{k-1}}}\right)

En posant $a$ valant respectivement $0$ , $½$ et $1$ , et connaissant les valeurs particulières des polynômes de Bernoulli en ces points, on retrouve immédiatement les équivalents en $z$ , $z + ½$ et $z + 1$ mentionnés plus hauts.

Histoire

La première occurrence d'un produit qui donnera naissance ultérieurement à la fonction gamma est due à Daniel Bernoulli[11] dans une lettre à Christian Goldbach.

En notation moderne[12]

x!=\lim _{n\rightarrow \infty }\left(n+1+{\frac {x}{2}}\right)^{x-1}\prod _{i=1}^{n}{\frac {i+1}{i+x}}

En 1729 également, Euler entreprend l'étude de ce produit et lui donne sa forme intégrale[13] - [14].

C'est Legendre qui, en 1811, note cette fonction $\Gamma$ , en apportant de nombreux compléments à son étude[13] - [15].

L'article de Borwein et Corless[16] passe en revue trois siècles de travaux mathématiques sur la fonction gamma.

Notes et références

Voir par exemple le début de ce devoir corrigé sur Wikiversité.
Pour le cas particulier où $z$ est un réel strictement positif, voir l'article Théorème de Bohr-Mollerup. Pour le cas général, voir cet exercice corrigé sur Wikiversité.
(de) O. Schlömilch, « Einiges über die Eulerischen Integrale der zweiten Art », Archiv der Mathematik und Physik, vol. 4,‎ 1844, p. 171 (lire en ligne).
(en) J. L. W. V. Jensen, « An elementary exposition of the theory of the Gamma function », Ann. of Math., 2^e série, vol. 17, n^o 3,‎ 1916, p. 124-166 (JSTOR 2007272) (p. 128).
« En 1844, 32 ans avant le célèbre travail de Weierstrass sur les fonctions entières » : (en) S. S. Dragomir, R. P. AgarwalRavi Agarwal et N. S. Barnett, « Inequalities for Beta and Gamma functions via some classical and new integral inequalities », J. Inequal. Appl. (nl), vol. 5, n^o 2,‎ 2000, p. 103-165 (lire en ligne) (p. 107).
(en) Jesús Guillera et Jonathan Sondow, « Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent », The Ramanujan Journal, vol. 16, n^o 3,‎ 2008, p. 247-270 (DOI 10.1007/s11139-007-9102-0, arXiv math/0506319).
(en) Karl Rawer, Wave Propagation in the Ionosphere, Dordrecht, Kluwer Academic Publishers, 1993.
D'après (de) O. R. Rocktäschel, Methoden zur Berechnung der Gammafunktion für komplexes Argument, université technologique de Dresde, 1922, thèse de doctorat.
(de) P. E. Böhmer, Differenzengleichungen und bestimmte Integrale, Leipzig, Köhler Verlag, 1939.
(en) Serge Lang, Complex Analysis, Springer, coll. « GTM » (n^o 103), 1998, 489 p. (ISBN 978-0-387-98592-3, lire en ligne), p. 418.
Paul Heinrich Fuss, Correspondance mathématique et physique de quelques célèbres géomètres du XVIII^e siècle, vol. II, St. Pétersbourg, Académie impériale des sciences, 1843 (lire en ligne), p. 324-325.
(en) Detlef Gronau, « Why is the gamma function so as it is? », Teaching Mathematics and Computer Science, vol. 1, n^o 1,‎ 2003, p. 43-53.
G. K. Srinivasan, « The Gamma function: An Eclectic Tour », The American Mathematical Monthly, vol. 114, n^o 4,‎ 2007, p. 297-315 (DOI 10.1080/00029890.2007.11920418)
L. Euler, « De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt », sur http://eulerarchive.maa.org
A.-M. Legendre, Exercices de calcul intégral sur divers ordres de transcendantes et sur les quadratures, t. 1, Vve Courcier (Paris), 1811 (lire en ligne), p. 221
(en) Jonathan M. Borwein et Robert M. Corless, Gamma and Factorial in the Monthly, 17 mars 2017 arXiv:1703.05349

Voir aussi

Bibliographie

N. Bourbaki, Éléments de mathématique, Livre IV, Fonctions d'une variable réelle, Berlin, Hermann, 1976 (réimpr. 2007) (1^re éd. 1949-1951) (ISBN 978-3-540-34036-2), chap. VII (« La fonction gamma »)
(en) Emil Artin, The Gamma Function, Dover, 2015 (1^re éd. 1964), 48 p. (lire en ligne)
Élémentaire et classique, traduit de (de) Einführung in die Theorie der Gammafunktion, 1931.
Jean Dieudonné, Calcul infinitésimal [détail des éditions]
p. 292-296 dans l'éd. Hermann de 1968
(en) Refaat El Attar, Special Functions and Orthogonal Polynomials, Lulu Press, 2006, 310 p. (ISBN 978-1-4116-6690-0, lire en ligne), p. 57-76
Maurice Godefroy, La fonction Gamma : théorie, histoire, bibliographie, Gauthier-Villars, 1901 (lire en ligne)
Thomas Joannes Stieltjes, « Sur le développement de $log Γ(a)$ », J. Math. Pures Appl., 4^e série, vol. 5,‎ 1889, p. 425-466 (lire en ligne)
(en) Edmund Taylor Whittaker et George Neville Watson, A Course of Modern Analysis, CUP, coll. « Cambridge Mathematrical Library », 1927 (réimpr. 1996), 4^e éd., 608 p. (ISBN 0-521-58807-3, lire en ligne), chap. XII (« The Gamma function »), p. 235-264

Liens externes

(en) Eric W. Weisstein, « Gamma Function », sur MathWorld
(en) R. A. Askey et R. Roy, « Gamma function », sur NIST Handbook of Mathematical Functions, Cambridge University Press, 2010 (ISBN 978-0521192255)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

Fonction gamma

Définition

Autres définitions

Propriétés

Lien avec la factorielle

Sur l'ensemble des réels

Sur le demi-plan complexe Re(z)>0

Autres propriétés

Formule des compléments

Formule de multiplication

Résidus

Dérivées

Lien avec les sommes de Gauss

Lien avec d'autres fonctions

Valeurs particulières

Formule asymptotique de Stirling

De Γ(z) et Γ(z+1)

De Γ(z+ ½)

Cas général

Histoire

Notes et références

Voir aussi

Articles connexes

Bibliographie

Liens externes

De $Γ(z)$ et $Γ(z +1)$

De $Γ(z + ½)$