Fonction zêta de Riemann

En mathématiques, la fonction zêta de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers. La position de ses zéros complexes est liée à la répartition des nombres premiers. Elle est aussi importante comme fonction modèle dans la théorie des séries de Dirichlet et se trouve au carrefour d'un grand nombre d'autres théories. Les questions qu'elle soulève sont loin d'être résolues et elle sert aussi de motivation et de fil conducteur à de nouvelles études, à l'instar du rôle joué par le grand théorème de Fermat.

La fonction zêta de Riemann

ζ(s)

dans le plan complexe. La couleur d'un point s code la valeur de

ζ(s)

: des couleurs vives indiquent des valeurs proches de 0 et la nuance indique l'argument de la valeur. Le point blanc pour s = 1 est le pôle ; les points noirs sur l'axe réel négatif (demi-droite horizontale) et sur la droite critique

Re(s)

1 / 2

(droite verticale) sont les zéros.

Carte des couleurs utilisées dans la figure du dessus.

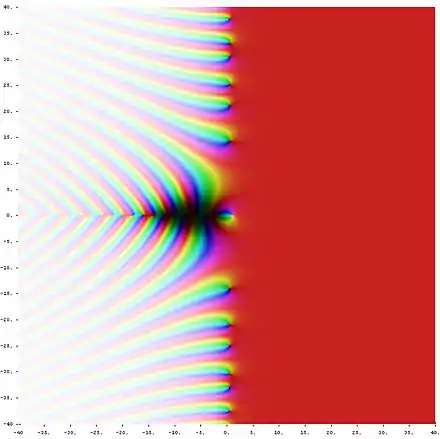
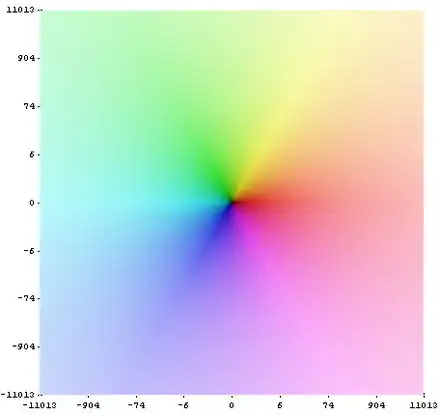
Premiers travaux sur la fonction zêta par Euler et Riemann

Article de Riemann de 1859 sur la fonction zêta.

Prologue

Le présent article commence par la définition de la fonction à partir de la série de Dirichlet puis cette définition est étendue au plan complexe privé de 1. On examine ensuite ce qui se passe en 1. La théorie de la fonction $ζ$ de Riemann définit trois régions dans le plan complexe, la région de convergence $Re(s)$ > 1, la bande critique 0 ≤ $Re$ (s) ≤ 1, et la région $Re(s)$ < 0. À partir de la relation fonctionnelle, le module de la fonction est estimé dans chacune de ces régions. Cela nécessite des formules permettant d'estimer la fonction ou d'autres fonctions qui lui sont liées. Puis on étudie les zéros. La relation fonctionnelle fournit les zéros réels et également l’ordre de ces zéros : ils sont simples. Dans la bande critique, il en existe une infinité. On estime donc ce nombre N(T) dans un rectangle de hauteur T. Le théorème de Hardy en place une infinité sur l'axe $Re(s)$ = $1 / 2$ . On estime, avec beaucoup de difficulté, le nombre N₀(T) des zéros dont la partie imaginaire est comprise entre 0 et T et dont la partie réelle est $1 / 2$ . Pour étudier la répartition des zéros, différentes quantités les faisant intervenir sont estimées. Enfin, les conjectures classiques sont examinées : définitions, conséquences, critères équivalents.

Les recherches sur la fonction zêta constituent un domaine très technique. La plupart des preuves, nécessitant une formation spécialisée en théorie analytique des nombres, sont omises ici.

La théorie de la fonction $ζ$ de Riemann est presque tout entière dominée par la question de la répartition de ses zéros. Comme l'explique la théorie générale des fonctions analytiques, toute fonction méromorphe s'écrit comme le produit de facteurs faisant apparaître les pôles et les zéros de cette fonction. L'hypothèse de Riemann selon laquelle tous les zéros non triviaux de la fonction $ζ$ de Riemann sont de partie réelle égale à $1 / 2$ renforce encore l'intérêt pour ces zéros. Aussi la théorie s'est-elle développée dans plusieurs directions : la première est celle de l'étude des zéros eux-mêmes. On a cherché à démontrer l'hypothèse de Riemann elle-même avant de se rendre compte des difficultés. L'objectif est alors devenu plus modeste : démontrer une partie de l'hypothèse de Riemann. D'un autre côté, la communauté mathématique croit en l'hypothèse de Riemann, aussi a-t-on cherché les conséquences de l'hypothèse de Riemann en prévision de sa démonstration. Cependant chaque nouvelle conséquence de l'hypothèse de Riemann est aussi une voie nouvelle pour l'infirmer.

Par exemple, on démontre que l'on a, sous l'hypothèse de Riemann, si $C > e 2γ$ (où $γ = 0,577\dots$ est la constante d'Euler-Mascheroni), pour t assez grand :

|\zeta (1+\mathrm {i} t)|\leq C\ln \ln t.

Si l'on démontrait l'existence d'une suite (t_n) tendant vers l'infini telle que

|\zeta (1+\mathrm {i} t_{n})|>C\ln \ln t_{n},

il en serait fini de l'hypothèse de Riemann.

Les conséquences de l'hypothèse de Riemann sont nombreuses. On a ainsi cherché à les démontrer indépendamment de cette hypothèse, ce qui s'avéra parfois possible. Et chacune de ces conséquences est devenue un objectif en soi. Devant la difficulté posée par la démonstration de l'hypothèse de Riemann, on a aussi énoncé des hypothèses plus faibles qu'on a également tenté de démontrer, sans beaucoup plus de succès.

Premières considérations sur la fonction

Définition par la série de Riemann

La fonction zêta de Riemann pour les réels s > 1.

La fonction $ζ$ de Riemann est une fonction analytique complexe méromorphe définie, pour tout nombre complexe s tel que $Re(s)$ > 1, par la série de Riemann :

\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+\cdots

D'après la théorie des séries de Dirichlet[note 1], on déduit que la fonction ainsi définie est analytique sur son domaine de convergence. La série ne converge pas en s = 1 car on a

\sum _{k=1}^{m}{\frac {1}{k}}\geq \int _{1}^{m+1}{\frac {\mathrm {d} u}{u}}=\ln(m+1)

qui tend vers l'infini avec $m$ (voir l'article détaillé « Série harmonique » pour d'autres démonstrations de ce résultat, et une estimation plus précise de la valeur des sommes partielles). La valeur s = 1 est donc une singularité de la fonction.

Valeurs de la fonction zêta pour s entier pair non nul

Euler a calculé (dans le cadre de sa solution au problème de Bâle) la valeur de la fonction $ζ$ pour les entiers strictement positifs pairs en utilisant l'expression de ${\frac {\sin x}{x}}$ sous forme de produit infini[note 2] ; il en a déduit la formule :

\zeta (2k)=\sum _{n=1}^{\infty }{\frac {1}{n^{2k}}}\ =\ {\frac {|B_{2k}|\ (2\pi )^{2k}}{2\,(2k)!}}

valable pour tout entier $k > 0$ , où les $B 2 k$ sont les nombres de Bernoulli ( $B_{0}=1,\quad B_{2}={\frac {1}{6}},\quad B_{4}=-{\frac {1}{30}},\quad B_{6}={\frac {1}{42}},\quad B_{8}=-{\frac {1}{30}},\quad \ldots$ ).

Ces valeurs de $ζ(2 k)$ s'expriment donc à l'aide des puissances paires de $π$ [1] :

\zeta (2)={\frac {\pi ^{2}}{6}}

[note 3]

{\displaystyle \quad

La formule $\zeta (2k)=\ {\frac {(-1)^{k-1}B_{2k}\ (2\pi )^{2k}}{2\,(2k)!}}$ s'étend à $k = 0$ avec $\zeta (0)=-{\frac {1}{2}}$ (voir infra).

On peut écrire le développement en série de Taylor : $-{\frac {x}{2}}\;\operatorname {cotan} {\frac {x}{2}}=-1+\sum _{n=1}^{\infty }|B_{2n}|{\frac {x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }2\zeta {(2n)}{\frac {x^{2n}}{(2\pi )^{2n}}},\,|x|<2\pi .$

On en déduit que la série génératrice des $ζ(2 k)$ pour $k \geq 0$ est donnée par :

\sum _{k\in \mathbb {N} }\zeta (2k)x^{2k}=-{\frac {\pi x}{2}}\cot(\pi x),\,|x|<1

Par exemple, on a : $\sum _{k\in \mathbb {N} }{\frac {\zeta (2k)}{2^{2k}}}=0$ , d'où on déduit la somme des séries : $\qquad \sum _{k=1}^{\infty }{\frac {\zeta (2k)}{2^{2k}}}={\frac {1}{2}}\qquad$ et $\qquad \sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{2^{2n}}}={\frac {1}{6}}$ .

Valeurs de la fonction zêta pour s entier impair

Pour les entiers impairs, le calcul n'est pas si simple. Ramanujan a beaucoup travaillé sur ces séries et Apéry a démontré en 1978 que $ζ(3)$ , qui vaut environ $1,202 056 9$ , est irrationnel (voir les articles « Constante d'Apéry » et « Théorème d'Apéry »).

En 2000, Tanguy Rivoal a démontré[2] qu'il existe une infinité de nombres irrationnels parmi les valeurs aux entiers impairs. En 2001, Wadim Zudilin (en) a démontré que l'un au moins des quatre nombres ζ(5), ζ(7), ζ(9) et ζ(11) est irrationnel[3].

On conjecture que toutes les valeurs aux entiers impairs sont irrationnelles et même algébriquement indépendantes sur ℚ( $π$ )[4], en particulier transcendantes.

Valeurs numériques particulières utilisées en physique

$\zeta \left({\frac {3}{2}}\right)\approx 2{,}612\;375$ .

Cette valeur est utilisée pour calculer la température critique d'un condensat de Bose-Einstein dans une boîte à frontière périodique, et pour l'onde de spin des systèmes magnétiques ;

$\zeta (2)=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}\approx 1{,}644\;934$ ;
$\zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+\cdots \approx 1{,}202\;056\;903.$

\zeta (3)

est la constante d'Apéry. Elle intervient dans la formule de la luminance photonique de la loi de Planck.

{\tilde {L}}_{\Omega }^{\circ }(T)={\frac {4\zeta (3)\mathrm {k} ^{3}}{\mathrm {h} ^{3}c^{2}}}\,T^{3}=4{,}840\times 10^{14}\,T^{3}

Unité : photons⋅s^-1⋅m^-2⋅sr^-1 ;

$\zeta (4)=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}\approx 1{,}082\;3$ .

Cette constante apparaît quand on intègre la loi de Planck pour obtenir la loi de Stefan-Boltzmann (en dimension 3) en physique.

La constante de Stefan-Boltzman en dimension n est donnée par la formule[5] :

\sigma _{n}=2n(n-1){\sqrt {4\pi }}^{\,n-2}\Gamma \left({\frac {n}{2}}\right)\zeta (n+1){\frac {\mathrm {k} ^{n+1}}{c^{n-1}\mathrm {h} ^{n}}}

où

Γ

est la fonction gamma,

h

est la constante de Planck,

c

la vitesse de la lumière dans le vide, et

k

la constante de Boltzmann.
En dimension 3 :

\sigma _{3}={\frac {2\pi ^{5}\mathrm {k} ^{4}}{15\mathrm {h} ^{3}c^{2}}}\approx 5{,}67\times 10^{-8}~\mathrm {W} \cdot \mathrm {m} ^{-2}\cdot \mathrm {K} ^{-4}.

Cette constante (appelée constante de Stefan-Boltzmann) est également utilisée dans le calcul de la limite basse température de la capacité thermique des solides dans le cadre du modèle de Debye.

Développements en série de Dirichlet en lien avec quelques fonctions arithmétiques

À partir de la série de Dirichlet de $ζ$ on démontre les formules suivantes[6] - [7], en faisant appel à la convolution de Dirichlet des fonctions arithmétiques qui vérifie :

\sum _{n=1}^{\infty }{\frac {f(n)}{n^{s}}}\sum _{n=1}^{\infty }{\frac {g(n)}{n^{s}}}=\sum _{n=1}^{\infty }{\frac {f*g(n)}{n^{s}}}

Si $Re(s)$ > 1,

\zeta ^{2}(s)=\sum _{n=1}^{\infty }{\frac {\tau (n)}{n^{s}}}

, où $τ$ est la fonction nombre de diviseurs (également notée d) :

\tau (n)=\sum _{d\mid n}1,

\zeta ^{2}(s)=1+{\dfrac {2}{2^{s}}}+{\dfrac {2}{3^{s}}}+{\dfrac {3}{4^{s}}}+{\dfrac {2}{5^{s}}}+{\dfrac {4}{6^{s}}}+{\dfrac {2}{7^{s}}}+\ldots ,

puisque $\tau ={\mathbf {1} }*{\mathbf {1} }.$

Si $Re(s)$ > 2,

\zeta (s)\zeta (s-1)=\sum _{n=1}^{\infty }{\frac {\sigma (n)}{n^{s}}}

, où $σ$ est la fonction somme des diviseurs :

\sigma (n)=\sum _{d\mid n}d

puisque $\sigma ={\rm {Id}}*{\mathbf {1} }.$

Les deux dernières formules sont des cas particuliers de l'égalité valide pour $Re(s) > max (1, Re(a) + 1)$ avec $a\in \mathbf {C}$

\zeta (s)\zeta (s-a)=\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}

, où

σ a

est la fonction somme des puissances a-ièmes des diviseurs:

\sigma _{a}(n)=\sum _{d\mid n}d^{a}

puisque $\sigma _{a}={\rm {Id}}^{a}*{\mathbf {1} }.$

Si $Re(s)$ > 1,

{\frac {1}{\zeta (s)}}=1-{\dfrac {1}{2^{s}}}-{\dfrac {1}{3^{s}}}-{\dfrac {1}{5^{s}}}+{\dfrac {1}{6^{s}}}-{\dfrac {1}{7^{s}}}+{\dfrac {1}{10^{s}}}-{\dfrac {1}{11^{s}}}+\ldots =\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}

, où $μ$ est la fonction de Möbius,

puisque $\delta _{1}={\mathbf {1} }*\mu .$

En 1899, La Vallée Poussin démontra qu'il existe une constante K telle que $\left|\sum _{n=1}^{x}{\frac {\mu (n)}{n}}\right|<{\frac {K}{\ln x}}$ , de sorte que la série précédente converge également pour s = 1, vers 0 :

0=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}=1-{\dfrac {1}{2}}-{\dfrac {1}{3}}-{\dfrac {1}{5}}+{\dfrac {1}{6}}-{\dfrac {1}{7}}+{\dfrac {1}{10}}-{\dfrac {1}{11}}-{\dfrac {1}{13}}+{\dfrac {1}{14}}+{\dfrac {1}{15}}-{\dfrac {1}{17}}-{\dfrac {1}{19}}+{\dfrac {1}{21}}+{\dfrac {1}{22}}+\ldots

Ce résultat, conjecturé par Euler, avait déjà été démontré par von Mangoldt en 1897[8]. Von Mangoldt utilise dans sa preuve le théorème des nombres premiers, démontré en 1896. Et ce dernier théorème est en fait équivalent à la convergence vers 0 de la série ci-dessus, comme l'a finalement établi Edmund Landau en 1911[9] - [10].

Si $Re(s)$ > 2,

{\frac {\zeta (s-1)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}

, où $φ$ est l'indicatrice d'Euler,

puisque l'indicatrice d'Euler φ vérifie l'égalité ${\rm {Id}}*\mu =\varphi .$

Cette formule est un cas particulier de l'égalité valide pour $Re(s) > k + 1$ avec $k\in \mathbf {N^{*}}$ ,

{\frac {\zeta (s-k)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {J_{k}(n)}{n^{s}}}

, où

J k

est la fonction totient de Jordan,

puisque $J_{k}=\mu *{\rm {Id}}^{k}$

Si $Re(s)$ > 1,

{\frac {\zeta (2s)}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\lambda (n)}{n^{s}}}

, où

λ

est la fonction de Liouville.

{\frac {\zeta (2s)}{\zeta (s)}}=1-{\frac {1}{2^{s}}}-{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}-{\frac {1}{5^{s}}}+{\frac {1}{6^{s}}}-{\frac {1}{7^{s}}}-{\frac {1}{8^{s}}}+{\frac {1}{9^{s}}}+{\frac {1}{10^{s}}}-\ldots

puisque la fonction de Liouville vérifie l'égalité ${\mathbf {1} }_{Q}*\mu =\lambda ,$ où ${\mathbf {1} }_{Q}$ est la fonction caractéristique (ou indicatrice) des carrés.

Si $Re(s)$ > 1,

{\frac {\zeta (s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {|\mu (n)|}{n^{s}}}=\sum _{n=1}^{\infty }{\frac {(\mu (n))^{2}}{n^{s}}}

, où

μ

est la fonction de Möbius,

puisque ${\mathbf {1} }={\mathbf {1} }_{Q}*|\mu |.$

Si $Re(s)$ > 1,

{\frac {\zeta ^{2}(s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {2^{\nu (n)}}{n^{s}}}

, où

ν

(n) désigne le nombre de facteurs premiers distincts de n,

puisque $\tau ={\mathbf {1} }_{Q}*2^{\nu }.$

Si $Re(s)$ > 1,

{\frac {\zeta ^{3}(s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {\tau (n^{2})}{n^{s}}}

, où

τ

est la fonction nombre de diviseurs (également notée d).

Si $Re(s)$ > 2,

{\frac {\zeta (s)\zeta (s-1)\zeta (s-2)}{\zeta (2s-2)}}=\sum _{n=1}^{\infty }{\frac {\sigma (n^{2})}{n^{s}}}.

Cette formule est un cas particulier de l'égalité valide pour $Re(s) > 1 + max (0, 2Re(a))$ avec $a\in \mathbf {C}$ ,

{\frac {\zeta (s)\zeta (s-a)\zeta (s-2a)}{\zeta (2s-2a)}}=\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n^{2})}{n^{s}}},

puisque ${\mathbf {1} }*{\rm {Id}}^{a}*{\rm {Id}}^{2a}=(\sigma _{a}\circ {\rm {Id}}^{2})*{\rm {Id}}_{Q}^{a}.$ où ${\rm {Id}}_{Q}^{a}={\mathbf {1} }_{Q}{\rm {Id}}^{a}$

Si $Re(s)$ > 1,

{\frac {\zeta ^{4}(s)}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {(\tau (n))^{2}}{n^{s}}}.

Cette formule est un cas particulier de l'égalité valide pour $Re(s) > 1$ et $\vartheta \in \mathbf {R}$ ,

{\frac {\zeta (s)^{2}\zeta (s+\mathrm {i} \vartheta )\zeta (s-\mathrm {i} \vartheta )}{\zeta (2s)}}=\sum _{n=1}^{\infty }{\frac {|\sigma _{\mathrm {i} \vartheta }(n)|^{2}}{n^{s}}}.

Les deux dernières formules sont des cas particuliers de la formule de Ramanujan[11] valable si $Re(s) > 1 + max (0, Re(a), Re(b), Re(a + b))$ avec $a\in \mathbf {C}$ et $b\in \mathbf {C}$ ,

{\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}}=\sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}},

ce qui se déduit de la relation ${\mathbf {1} }*{\rm {Id}}^{a}*{\rm {Id}}^{b}*{\rm {Id}}^{a+b}=(\sigma _{a}\sigma _{b})*{\rm {Id}}_{Q}^{{\frac {a}{2}}+{\frac {b}{2}}}.$

Produit eulérien

Leonhard Euler par Emanuel Handmann.

Le lien entre la fonction $ζ$ et les nombres premiers avait déjà été établi par Leonhard Euler avec la formule, valable pour $Re(s)$ > 1 :

\zeta (s)\ =\ \prod _{p\in {\mathcal {P}}}\ {\frac {1}{1-p^{-s}}}={\frac {1}{\left(1-{\frac {1}{2^{s}}}\right)\left(1-{\frac {1}{3^{s}}}\right)\left(1-{\frac {1}{5^{s}}}\right)\cdots }}

où le produit infini est étendu à l'ensemble $\scriptstyle {\mathcal {P}}$ des nombres premiers. Cette relation est une conséquence de la formule pour les suites géométriques et du théorème fondamental de l'arithmétique. On appelle parfois cette formule produit eulérien.

Lien avec la répartition des nombres premiers

Un autre lien existe avec cette fois la fonction de comptage $π(x)$ des nombres premiers inférieurs ou égaux à $x$ :

\pi (x)=\sum _{p\in {\mathcal {P}},p\leq x}1.

On a en effet, pour $Re(s)$ > 1 :

\ln \zeta (s)=s\int _{2}^{\infty }{{\frac {\pi (u)}{u(u^{s}-1)}}\mathrm {d} u}.

En fait, la position des zéros de la fonction $ζ$ de Riemann fournit la position des nombres premiers. On peut même trouver une formule exprimant chaque nombre premier en fonction des zéros de la fonction $ζ$ de Riemann.

Expression intégrale

On a la formule intégrale, classique depuis Euler, valide si $Re(s)$ > 1 :

\zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{1}{\frac {(-\ln u)^{s-1}}{1-u}}\,\mathrm {d} u

où $Γ$ désigne la fonction gamma, ce qui (par changement de variable) équivaut à :

\zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{+\infty }{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\,\mathrm {d} t

On peut voir cette formule comme un cas particulier d'une transformation générale aux séries de Dirichlet[12]. Elle se traduit en disant que la fonction $s\mapsto \zeta (s)\operatorname {\Gamma } (s)$ est la transformation de Mellin[13] de la fonction $t\mapsto {\frac {1}{\mathrm {e} ^{t}-1}}$ .

Dérivées de la fonction zêta

Une expression de la dérivée de la fonction $ζ$ est donnée par la série de Dirichlet, convergente si $Re(s)$ > 1 :

\zeta '(s)={\frac {\mathrm {d} }{\mathrm {d} s}}\left(1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+\cdots \right)=-\left({\frac {\ln 2}{2^{s}}}+{\frac {\ln 3}{3^{s}}}+{\frac {\ln 4}{4^{s}}}+\cdots \right)=-\sum _{n=2}^{\infty }{\frac {\ln n}{n^{s}}}.

La dérivée d'ordre k est donnée par :

\zeta ^{(k)}(s)=(-1)^{k}\,\sum _{n=2}^{\infty }{\frac {(\ln n)^{k}}{n^{s}}}.

Que devient la série de Riemann sur l'axe $Re(s)$ = 1 ?

La théorie des séries de Dirichlet montre que pour $s = σ + i t$ , la série de Riemann $\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}$ diverge grossièrement si $σ \leq 0$ , converge absolument si $σ > 1$ et diverge si $t = 0$ et $σ \in ]0, 1]$ .

Dans le cas restant ( $σ \in ]0, 1]$ mais $t \neq 0$ ), pour montrer qu'elle diverge aussi et préciser comment, il suffit d'affiner un peu la comparaison série-intégrale :

\sum _{n=1}^{N}{\frac {1}{n^{s}}}-\int _{1}^{N+1}{\frac {{\rm {d}}u}{u^{s}}}=\sum _{n=1}^{N}\left({\frac {1}{n^{s}}}-\int _{n}^{n+1}{\frac {{\rm {d}}u}{u^{s}}}\right)

\left|{\frac {1}{n^{s}}}-\int _{n}^{n+1}{\frac {{\rm {d}}u}{u^{s}}}\right|=\left|\int _{n}^{n+1}\int _{n}^{u}{\frac {s{\rm {d}}v}{v^{s+1}}}{\rm {d}}u\right|\leq {\frac {|s|}{n^{\sigma +1}}}

donc la série correspondante converge. Quant à l'intégrale $\int _{1}^{N+1}{\frac {{\rm {d}}u}{u^{s}}}$ , elle est égale, à une constante près, à ${\frac {(N+1)^{1-s}}{1-s}}$ , de module ${\frac {(N+1)^{1-\sigma }}{\sqrt {(1-\sigma )^{2}+t^{2}}}}$ .

si $0 < σ < 1$ , il en résulte que lorsque $N$ tend vers l'infini, ce terme prend des oscillations de plus en plus importantes : la série diverge.
si $σ = 1$ (et $t \neq 0$ ), le module devient égal à $1 / | t |$ , mais l'argument ( $mod 2π$ ) ne tend pas vers une constante : la série diverge mais ses oscillations restent bornées par $1 / | t |$ .

Extension à ℂ \ {1}

La fonction $ζ$ admet un prolongement analytique à tout le plan complexe, sauf $1$ . Il existe plusieurs démonstrations, faisant appel à différentes représentations de la fonction $ζ$ .

Par la formule d'Euler-Maclaurin

La formule d'Euler-Maclaurin[14], appliquée à la fonction $x \mapsto x -s$ sur l'intervalle [1, N], donne pour tout entier n différent de 0 :

\sum _{r=1}^{N}r^{-s}={{1-N^{1-s}} \over {s-1}}+{{1+N^{-s}} \over 2}+\sum _{k=2}^{n}B_{k}{\frac {s(s+1)\dots (s+k-2)}{k!}}(1-N^{-s-k+1})-R_{n,N}(s),

où les coefficients $B k$ sont les nombres de Bernoulli (ils sont nuls si k est impair et différent de 1),

R_{n,N}(s)={1 \over {n!}}s(s+1)\dots (s+n-1)\int _{1}^{N}B_{n}(x-[x])x^{-s-n}\mathrm {d} x,

où les $B n (x)$ sont les polynômes de Bernoulli et où $[x]$ désigne la partie entière de $x$ .

En faisant tendre N vers l'infini et en restant dans le demi-plan $Re(s)$ > 1, on en déduit pour tout entier n = 1, 2, 3… que

\zeta (s)={1 \over {s-1}}+{1 \over 2}+\sum _{k=2}^{n}B_{k}{\frac {s(s+1)\dots (s+k-2)}{k!}}-{\frac {s(s+1)\dots (s+n-1)}{n!}}\int _{1}^{\infty }B_{n}(x-[x])x^{-s-n}\mathrm {d} x.

Les fonctions $x \mapsto B n (x - [x])$ étant périodiques et polynomiales sur [0 ; 1[, elles restent bornées sur l'intervalle d'intégration, donc l'intégrale à droite converge si $Re(s)$ > 1 – n. Donc le membre de droite définit, sur $Re(s)$ > 1 – n, une fonction $ζ$ _n, holomorphe en dehors de 1, qui prolonge $ζ$ . L'unicité du prolongement analytique montre que les fonctions $ζ$ _n et $ζ$ _{n + 1} sont identiques sur $Re(s)$ > 1 – n. Ces identités permettent donc de définir une unique fonction méromorphe sur tout le plan complexe (avec un seul pôle en 1), coïncidant avec la fonction $ζ$ déjà définie pour $Re(s)$ > 1 et qu'on appelle encore $ζ$ .

Par une intégrale sur ℝ⁺

On part de l'expression intégrale vue plus haut, pour tout complexe s tel que $Re(s)$ > 1 :

\Gamma (s)\zeta (s)=\int _{0}^{\infty }{\frac {t^{s-1}}{{\rm {e}}^{t}-1}}\mathrm {d} t.

Le prolongement analytique est réalisé[note 4] en écrivant

\Gamma (s)\zeta (s)=\int _{0}^{1}{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\mathrm {d} t+\int _{1}^{\infty }{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\mathrm {d} t.

La seconde intégrale est une fonction holomorphe de s. On décompose en série de Taylor dans la première. Les $B n$ désignant les nombres de Bernoulli, comme on a, pour tout t tel que | t | < 2 $π$

{\frac {t}{{\rm {e}}^{t}-1}}=\sum _{n=0}^{\infty }{\frac {B_{n}t^{n}}{n!}},

en remplaçant dans la première intégrale et en intégrant terme à terme, on trouve

\zeta (s)={\frac {1}{(s-1)\Gamma (s)}}+{\frac {1}{\Gamma (s)}}\sum _{n=1}^{\infty }{\frac {B_{n}}{n!(n+s-1)}}+{\frac {1}{\Gamma (s)}}\int _{1}^{\infty }{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\mathrm {d} t.

La série est convergente et définit une fonction holomorphe partout sauf aux entiers négatifs ou nuls (car pour s différent de ces valeurs, le rayon de convergence de la série entière de coefficients $B n /n!$ n'est pas modifié lorsqu'on divise ces coefficients par les n + s – 1) et de même, au voisinage d'un entier négatif – k, elle est la somme d'une fonction holomorphe et du terme ${\frac {B_{k+1}}{(k+1)!~(s+k)}}.$

Quand s tend vers – k, $Γ$ (s) ayant un pôle simple en s = – k , $ζ(s)$ est par conséquent la somme d'une fonction qui tend vers 0 et du terme :

{\frac {1}{\Gamma (s)}}~{\frac {B_{k+1}}{(k+1)!~(s+k)}}~{\underset {\overset {s\to -k}{}}{\sim }}~{\frac {s+k}{{\text{Res}}(\Gamma ,-k)}}~{\frac {B_{k+1}}{(k+1)!~(s+k)}}=(-1)^{k}~k!~{\frac {B_{k+1}}{(k+1)!}}.

Ainsi, le prolongement méromorphe de $ζ$ à tout le plan complexe n'a de pôle qu'au point 1, et l'on obtient au passage la formule d'Euler[note 5] :

\zeta (-k)=(-1)^{k}{\frac {B_{k+1}}{k+1}}

Par une intégrale de contour

La fonction $ζ(s)$ se prolonge aussi analytiquement par l'intégrale

\zeta (s)={\frac {\mathrm {e} ^{-\mathrm {i} \pi s}\Gamma (1-s)}{2\mathrm {i} \pi }}\oint _{C}{{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u},

$Γ$ étant la fonction gamma.

$C$ désigne un lacet longeant l'axe réel et englobant 0 parcouru de $+\infty$ à $+\infty$ dans le sens trigonométrique.

Une fois cette formule démontrée initialement pour $Re(s)$ > 1, l'expression à droite restant valable pour toute valeur bornée de s définit donc une fonction analytique. D'après le théorème du prolongement analytique, elle représente le prolongement (sauf en s = 1) de la fonction $ζ$ .

Démonstration

On part à nouveau de l'expression intégrale vue plus haut, pour tout complexe s tel que $Re(s)$ > 1 :

\zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{+\infty }{\frac {t^{s-1}}{\mathrm {e} ^{t}-1}}\mathrm {d} t.

D'une autre part, on considère la fonction $h$ sur l'ensemble $D_{\zeta }:=\{s\in \mathbf {C} \mid {\text{Re}}(s)>1\}$ par :

h(s)=\oint _{C_{\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u

avec $C_{\nu }=C_{1,\nu }\cup C_{2,\nu }\cup C_{3,\nu }$ le lacet décrit ainsi :

$C_{1,\nu }$ : demi-droite dont les points ont pour argument 0, décrite de $+\infty$ à $ν$ .

$C_{2,\nu }$ : cercle de rayon $ν$ et de centre 0, dont l'argument des points croit de 0 à $2π$ .

$C_{3,\nu }$ : demi-droite dont les points ont pour argument $2π$ , décrite de $ν$ à $+\infty$ .

alors pour que $h$ soit holomorphe sur tout le plan complexe on prend $0 < ν < 2π$ (voir que $e u - 1$ ne s'annule pas si $ν$ est défini ainsi) donc :

h(s)=\int _{C_{1,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u+\int _{C_{2,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u+\int _{C_{3,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u

D'une part il est clair que :

\int _{C_{1,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u=\int _{+\infty }^{\nu }{\frac {r^{s-1}}{\mathrm {e} ^{r}-1}}\mathrm {d} r

alors :

\lim _{\nu \to 0}\int _{C_{1,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u=-\int _{0}^{+\infty }{\frac {r^{s-1}}{\mathrm {e} ^{r}-1}}\mathrm {d} r=-\zeta (s)\Gamma (s)

et que :

\int _{C_{2,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u={\mathcal {O}}\left(\nu ^{{\text{Re}}(s)-1}\right)

ce qui entraîne le fait que :

\lim _{\nu \to 0}\int _{C_{2,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u=0

et enfin que :

\int _{C_{3,\nu }}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}\mathrm {d} u=\int _{\nu }^{+\infty }{\frac {r^{s-1}\mathrm {e} ^{2\mathrm {i} \pi (s-1)}}{\mathrm {e} ^{r}-1}}\mathrm {d} r{\underset {\nu \to 0}{\longrightarrow }}\mathrm {e} ^{2\mathrm {i} \pi (s-1)}\zeta (s)\Gamma (s)

et puisque la fonction $h$ est indépendante de $ν$ alors :

h(s)=\left(\mathrm {e} ^{2\mathrm {i} \pi (s-1)}-1\right)\zeta (s)\Gamma (s).

En utilisant les formules d'Euler on trouve que :

\mathrm {e} ^{2\mathrm {i} \pi (s-1)}-1=2\mathrm {i} \sin(\pi (s-1))\mathrm {e} ^{\mathrm {i} \pi (s-1)}=2\mathrm {i} \sin(\pi s)\mathrm {e} ^{\mathrm {i} \pi s}

alors en substituant l'expression on aura :

h(s)=2\mathrm {i} \mathrm {e} ^{\mathrm {i} \pi s}\sin(\pi s)\zeta (s)\Gamma (s)

et d'un autre côté, d'après la formule des compléments de la fonction gamma, on a pour tout s tel que $Re(s)$ ∈ ]0, 1[

\Gamma (s)\sin(\pi s)={\frac {\pi }{\Gamma (1-s)}}

d'où :

h(s)=2\pi \mathrm {i} \mathrm {e} ^{\mathrm {i} \pi s}{\frac {\zeta (s)}{\Gamma (1-s)}}

finalement :

\zeta (s)={\frac {\mathrm {e} ^{-\mathrm {i} \pi s}\Gamma (1-s)}{2\mathrm {i} \pi }}h(s)={\frac {\mathrm {e} ^{-\mathrm {i} \pi s}\Gamma (1-s)}{2\mathrm {i} \pi }}\oint _{C}{\frac {u^{s-1}}{\mathrm {e} ^{u}-1}}~\mathrm {d} u

et puisque $h$ est holomorphe sur tout le plan ce qui implique le prolongement de la fonction $ζ$ en fonction méromorphe dans ℂ.

Par la formule sommatoire d'Abel

Utilisant la formule sommatoire d'Abel, on trouve pour $Re(s)$ > 1,

\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=s\int _{1}^{\infty }{{\frac {[u]}{u^{1+s}}}\mathrm {d} u}.

La partie entière $[u]$ se décompose en $u - {u}$ , où ${u}$ désigne la partie fractionnaire de $u$ . On a alors :

\zeta (s)={\frac {s}{s-1}}-s\int _{1}^{\infty }{{\frac {\{u\}}{u^{1+s}}}\mathrm {d} u}.

Comme ${u}$ est toujours compris entre 0 et 1, l'intégrale est convergente pour $Re(s)$ > 0. À partir du prolongement pour $Re(s)$ > 0 et en appliquant la relation fonctionnelle (valide pour 0 < $Re(s)$ < 1, voir plus loin), on obtient le prolongement pour $Re(s)$ ≤ 0 (sauf en s = 0).

Par la fonction êta de Dirichlet

On peut encore étendre la fonction $ζ$ sur $Re(s)$ > 0 à partir de la définition de la série alternée (appelée fonction êta de Dirichlet) :

\eta (s)=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n^{s}}}=1-{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}-{\frac {1}{4^{s}}}+{\frac {1}{5^{s}}}-{\frac {1}{6^{s}}}+{\frac {1}{7^{s}}}-{\frac {1}{8^{s}}}+\cdots

Cette série est convergente pour s réel strictement positif, par application du critère des séries alternées ; il en est en fait de même pour $Re(s)$ > 0, ce qui se démontre en utilisant le lemme d'Abel (on peut aussi montrer plus simplement la convergence absolue de la série $\sum _{n=1}^{\infty }{\frac {(2n)^{s}-(2n-1)^{s}}{(2n)^{s}(2n-1)^{s}}}$ ).

{\text{Si}}\quad {\text{Re}}(s)>1,\qquad \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\eta (s)+2\sum _{n=1}^{\infty }{\frac {1}{(2n)^{s}}}=\eta (s)+{\frac {2}{2^{s}}}\zeta (s),\quad {\text{donc}}

[note 6]

{\displaystyle

[15]

\zeta (s)={\frac {\eta (s)}{1-2^{1-s}}}.

Cela réalise ainsi le prolongement de la fonction $ζ$ sur $Re(s)$ > 0, sauf pour

s=1+\mathrm {i} {\frac {2k\pi }{\ln(2)}}\qquad (k\in \mathbb {Z} )

qui sont les zéros de 1 – 2^{1 – s}.

À partir du prolongement pour $Re(s)$ > 0 et en appliquant la relation fonctionnelle (voir plus loin), on obtient le prolongement partout sauf en ces points.

Pour ces points, on peut appliquer soit la série de Dirichlet de $1 / ζ$ , qui converge sur $Re(s)$ = 1, soit une autre relation du même genre[16].

De ce que

0<{\frac {1}{3n-2}}+{\frac {1}{3n-1}}-{\frac {2}{3n}}={\frac {1}{3n^{2}}}+O\left({\frac {1}{n^{3}}}\right),

où O est la notation de Landau, on déduit que la série[17]

\zeta _{3}(s)=\sum _{n=1}^{\infty }{\left({\frac {1}{(3n-2)^{s}}}+{\frac {1}{(3n-1)^{s}}}-{\frac {2}{(3n)^{s}}}\right)}=1+{\frac {1}{2^{s}}}-{\frac {2}{3^{s}}}+{\frac {1}{4^{s}}}+{\frac {1}{5^{s}}}-{\frac {2}{6^{s}}}+{\frac {1}{7^{s}}}+{\frac {1}{8^{s}}}-{\frac {2}{9^{s}}}+\cdots

est convergente pour $Re(s)$ = 1[note 7]. En procédant comme pour la fonction $η$ , on montre que :

\zeta (s)={\frac {\zeta _{3}(s)}{1-{3^{1-s}}}}.

Il suffit donc de calculer la série seulement pour ces points car $ln 3 / ln 2$ se trouvant irrationnel, le dénominateur 1 – 3^{1 – s} ne peut être nul en même temps que 1 – 2^{1 – s} (sauf pour s = 1).

La fonction êta vérifie également

\eta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{\mathrm {e} ^{x}+1}}~\mathrm {d} x.

On déduit, pour $Re(s)$ > 0, sous réserve de ce qui a été dit pour le prolongement par la fonction êta de Dirichlet pour les points $s = 1 + 2i k π/ln(2)$ , l'expression intégrale :

\zeta (s)={\frac {1}{(1-2^{1-s})\Gamma (s)}}\int _{0}^{1}{\frac {|\ln u|^{s-1}}{1+u}}\mathrm {d} u.

\zeta (s)={\frac {1}{(1-2^{1-s})\Gamma (s)}}\int _{0}^{+\infty }{\frac {t^{s-1}}{1+\mathrm {e} ^{t}}}\,\mathrm {d} t.

Par la formule de Landau ou celle de Ramaswami

Dans les formules précédentes, il est à remarquer que le prolongement ne s'obtient que dans une portion du plan et qu'il faut utiliser la relation fonctionnelle pour avoir un prolongement au plan tout entier. Les deux formules qui suivent n'ont pas ce défaut. Ces deux autres méthodes de prolongement de $ζ$ , sans conteste les plus simples, sont fondées, chacune, sur une formule exprimant $ζ(s)$ en fonction de $ζ$ (s + 1), $ζ$ (s + 2), …

On a ainsi la formule publiée par Edmund Landau :

\zeta (s)-{\frac {1}{s-1}}=1-s{\frac {\zeta (s+1)-1}{2!}}-s(s+1){\frac {\zeta (s+2)-1}{3!}}-s(s+1)(s+2){\frac {\zeta (s+3)-1}{4!}}-\ldots

\zeta (s)-{\frac {1}{s-1}}=1-\sum _{k=1}^{\infty }s^{\overline {k}}\,{\frac {\zeta (s+k)-1}{(k+1)!}}\!

$s^{\overline {k}}$ étant la factorielle croissante. La démonstration se fait en écrivant que $s^{\overline {k}}\,{\frac {\zeta (s+k)-1}{(k+1)!}}={\frac {1}{1-s}}{1-s \choose k+1}\sum _{n=2}^{\infty }n^{1-s-(k+1)}$ puis en inversant $\sum _{k}$ et $\sum _{n}$ et en utilisant la série binomiale $(1+{\frac {1}{n}})^{1-s}=\sum _{k=0}^{\infty }{1-s \choose k}n^{-k}$ .

On a aussi la formule de Ramaswami[18] - [note 8] :

\eta (s)=(1-2^{1-s})\zeta (s)={\frac {s}{1!}}{\frac {\zeta (s+1)}{2^{s+1}}}+{\frac {s(s+1)}{2!}}{\frac {\zeta (s+2)}{2^{s+2}}}+{\frac {s(s+1)(s+2)}{3!}}{\frac {\zeta (s+3)}{2^{s+3}}}+\ldots

(1-2^{1-s})\zeta (s)=\sum _{n=1}^{\infty }{\frac {s^{\overline {n}}}{n!}}{\frac {\zeta (s+n)}{2^{s+n}}}.

Le prolongement analytique s'effectue par bandes de largeur 1. La série de Dirichlet étant absolument convergente sur $Re(s)$ > 1, la formule choisie prolonge sur $Re(s)$ > 0. En appliquant à nouveau la formule, on prolonge à $Re(s)$ > –1, et ainsi de suite.

Propriétés diverses de la fonction

Comportement asymptotique

Au voisinage de $+\infty$ (sur l'axe réel), on a

$\zeta (s)=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots +{\frac {1}{n^{s}}}+o({\frac {1}{n^{s}}})$

(on obtient ce développement en comparant le reste de la série à l'intégrale $\int _{n}^{\infty }{{\frac {1}{u^{s}}}\mathrm {d} u}$ )

Développement de Laurent au voisinage de 1

Thomas Joannes Stieltjes s'intéressa de près à la fonction

ζ

de Riemann. Il est l'auteur d'une tentative avortée de démonstration de l'hypothèse de Riemann à partir d'une hypothèse voisine de celle de Mertens qu'il fut incapable de démontrer.

On a vu plus haut que :

\zeta (s)={\frac {s}{s-1}}-s\int _{1}^{\infty }{{\frac {\{u\}}{u^{1+s}}}\mathrm {d} u}

Comme ${u}$ est toujours compris entre 0 et 1, l'intégrale est convergente et le terme est borné. Le premier terme vaut aussi ${\frac {s}{s-1}}={\frac {1}{s-1}}+1$ , ce qui montre que la fonction $ζ$ admet un pôle d'ordre 1 en $1$ et de résidu $1$ . Cela constitue le théorème de Dirichlet. Le développement en série de Laurent de la fonction $ζ(s)$ s'écrit donc

\zeta (s)={\frac {1}{s-1}}+\sum _{n=0}^{\infty }{(-1)^{n}{\frac {\gamma _{n}}{n!}}(s-1)^{n}}

Les coefficients $\gamma _{n}$ , appelés constantes de Stieltjes ou nombres de Stieltjes, sont donnés par[19] :

\gamma _{n}=\lim _{N\to \infty }\left({\sum _{k=1}^{N}{{\frac {(\ln k)^{n}}{k}}-{\frac {(\ln N)^{n+1}}{n+1}}}}\right)

En particulier, $\gamma _{0}$ est la constante d'Euler-Mascheroni : $\gamma _{0}=\gamma =0{,}5772\ldots$ .

Matsuoka, en 1985[20], a montré que :

\forall n>4\quad |\gamma _{n}|\leq 10^{-4}(\ln n)^{n}

On sait aussi qu'asymptotiquement, la moitié de ces nombres sont positifs.

L'équivalent $\zeta (s)\sim _{1}{\frac {1}{s-1}}$ montre que $ζ$ est négative sur l'axe réel juste avant $1$ [note 9] (elle est positive après $1$ de manière élémentaire puisque tous les termes de la série de Dirichlet sont alors positifs).

Le développement de Laurent à l'ordre 0, $\zeta (1+\varepsilon )={\frac {1}{\varepsilon }}+\gamma +o(1)$ , donne la « valeur principale de Cauchy de la fonction » en $1$ :

\lim _{\varepsilon \to 0}{\frac {\zeta (1+\varepsilon )+\zeta (1-\varepsilon )}{2}}=\gamma

Relation fonctionnelle

La fonction $ζ$ satisfait à l'équation fonctionnelle :

\zeta (s)=2^{s}\pi ^{s-1}\sin \left({\frac {\pi s}{2}}\right)\Gamma (1-s)\zeta (1-s)

valable pour tout nombre complexe s différent de 0 et 1, démontrée par Riemann en 1859. Ici, $Γ$ désigne la fonction gamma.

Démonstration

Une démonstration, parmi de nombreuses autres, a été donnée par Luis Báez-Duarte en 2003[21]. Elle est particulièrement courte. On part de la formule intégrale résultant de la formule sommatoire d'Abel (attention la borne inférieure est prise à 0, non à 1)

-{\frac {\zeta (s)}{s}}=\int _{0}^{\infty }u^{-s-1}\{u\}\,\mathrm {d} u

cette égalité étant valable pour $Re(s) \in ]0, 1[$ .

Avec le changement de variable $u=2v$ , on obtient $-2^{s}{\frac {\zeta (s)}{s}}=\int _{0}^{\infty }v^{-s-1}\{2v\}\,\mathrm {d} v$ donc

(2^{s}-1){\frac {\zeta (s)}{s}}=\int _{0}^{\infty }u^{-s-1}(\{u\}-\{2u\})\,\mathrm {d} u

On utilise alors la série de Fourier $\{x\}={\frac {1}{2}}-\sum _{n=1}^{\infty }{\frac {\sin(2n\pi x)}{n\pi }}$ (pour $x$ non entier), qui donne

(2^{s}-1){\frac {\zeta (s)}{s}}=\int _{0}^{\infty }u^{-s-1}\sum _{n=1}^{\infty }{\frac {\sin(4n\pi u)-\sin(2n\pi u)}{n\pi }}\,\mathrm {d} u

Les sommes partielles étant uniformément bornées, on peut intervertir $\sum$ et $\int$ : pour $Re(s) \in ]0, 1[$ ,

{\begin{aligned}(2^{s}-1){\frac {\zeta (s)}{s}}&=\sum _{n=1}^{\infty }{\frac {1}{n\pi }}\int _{0}^{\infty }u^{-s-1}\left(\sin(4n\pi u)-\sin(2n\pi u)\right)\,\mathrm {d} u\\&=\sum _{n=1}^{\infty }{\frac {(2n\pi )^{s}}{n\pi }}\int _{0}^{\infty }t^{-s-1}\left(\sin(2t)-\sin(t)\right)\,\mathrm {d} t\\&=2^{s}\pi ^{s-1}\zeta (1-s)(2^{s}-1)\sin \left({\frac {-\pi s}{2}}\right)\Gamma (-s),\end{aligned}}

la dernière égalité étant valide a priori pour $Re(s) \in ]-1, 0[$ , mais restant vraie pour $Re(s) \in ]0, 1[$ , par prolongement analytique.

On obtient alors

(2^{s}-1)\zeta (s)=-s(2^{s}-1)2^{s}\pi ^{s-1}\Gamma (-s)\sin \left({\frac {\pi s}{2}}\right)\zeta (1-s).

dont on déduit la relation fonctionnelle pour $Re(s)$ ∈ ]0, 1[. On l'étend à ℂ\{0, 1} par prolongement analytique.

Représentation de la fonction zêta sur l'axe des réels entre –7 et 7.

De la relation fonctionnelle, on déduit que, pour s différent de 0 et de 1 :

\zeta (1-s)={2 \over (2\pi )^{s}}\,\cos \left({\frac {\pi s}{2}}\right)\,\Gamma (s)\,\zeta (s).

La fonction $ξ$ définie pour s différent de 0 et de 1 par

\xi (s)={\frac {1}{2}}s(s-1)\pi ^{-s/2}\Gamma (s/2)\zeta (s)\quad

vérifie

\displaystyle \xi (s)=\xi (1-s).

On en déduit que la fonction

\Xi (\sigma )=\xi \left({\frac {1}{2}}+\mathrm {i} \sigma \right)

est paire : $Ξ(s) = Ξ(- s)$ .

On retrouvera ces deux fonctions dans l'étude des zéros non triviaux de $ζ$ .

Valeurs de la fonction zêta pour s entier négatif ou nul

Valeurs de la fonction zêta entre –14 et –0,9.

De la définition de la fonction zêta par une intégrale sur ℝ⁺, on a déduit[22] que pour tout entier naturel $n$ , $ζ(- n)$ est le nombre rationnel suivant :

\zeta (-n)=(-1)^{n}{\frac {B_{n+1}}{n+1}}

où $B n + 1$ est un nombre de Bernoulli.

Pour $n$ = 0, on a :

\zeta (0)=B_{1}=-{\frac {1}{2}}.

Si $n$ est pair mais non nul, le nombre de Bernoulli $B n + 1$ est nul, d'où, avec $n = 2 k$ et $k > 0$ :

\zeta (-2k)={\frac {B_{2k+1}}{2k+1}}=0.

\zeta (-2)=\zeta (-4)=\zeta (-6)=\zeta (-8)=\ldots =0.

Si $n$ est impair, $n = 2 k - 1$ avec $k > 0$ :

\zeta (-(2k-1))=-{\frac {B_{2k}}{2k}}.

Par exemple :

\zeta (-1)=-{\frac {B_{2}}{2}}=-{\frac {1}{12}},

C'est cette relation que Ramanujan écrivit en 1910 dans un article du Journal of the Indian Mathematical Society sous la forme[23] :

1+2+3+4+5+\ldots =-{\frac {1}{12}}.

{\displaystyle \zeta (-3)=-{\frac {B_{4}}{4}}={\frac {1}{120}}\quad

Définition de $ln ζ$ et de sa dérivée

La fonction $ζ$ étant réelle sur l'axe réel et plus grande que 1, le logarithme de cette valeur existe et est réel. Il est donc naturel de choisir, parmi l'infinité des définitions possibles du logarithme d'une fonction analytique, celle qui prolonge le logarithme naturel sur la demi-droite $]1, +\infty[$ . On prolonge donc par continuité les valeurs de $ln ζ$ qui sont réelles sur $]1, +\infty[$ .

Présentation élémentaire pour les nombres complexes du demi-plan Re(s) > 1

On part de la formule du produit eulérien, dont on sait qu'il converge pour tout s dans $Re(s)$ > 1. On peut se limiter à considérer dans un premier temps s = σ réel. On prend le logarithme du produit. Cela a un sens puisque $ζ$ (σ) ne s'annule pas sur σ > 1. On a alors

\ln \zeta (\sigma )=-\sum _{p\in {\mathcal {P}}}\ln \left(1-{\frac {1}{p^{\sigma }}}\right).

Il reste à développer le logarithme en série entière, ce qui est possible puisque p ≥ 2 et σ > 1. Cela justifie que l'on définisse, pour tout complexe s satisfaisant $Re(s)$ > 1 la série :

D(s)=\sum _{p\in {\mathcal {P}}}\sum _{\nu \geq 1}{\frac {1}{\nu p^{\nu s}}}.

Cette série, normalement convergente sur tout compact du demi-plan $Re(s)$ > 1, définit une fonction holomorphe sur ce demi-plan.

Si s = σ > 1 est réel, alors $\sum _{\nu \geq 1}{\frac {1}{\nu p^{\nu s}}}=-\ln \left(1-{\frac {1}{p^{\sigma }}}\right)$ où $ln$ est le logarithme réel habituel. On en déduit que $e D (σ) = ζ(σ)$ . Les deux fonctions $e D$ et $ζ$ sont holomorphes sur $Re(s)$ > 1 et elles coïncident sur la demi-droite $]1, +\infty[$ . Par le principe de prolongement holomorphe, on a donc

\mathrm {e} ^{D(s)}=\zeta (s)\

pour tout complexe s tel que $Re(s)$ > 1. Par dérivation de l'égalité précédente, on obtient immédiatement $D'(s)={\frac {\zeta '(s)}{\zeta (s)}}$ . En dérivant la série définissant D, on obtient :

D'(s)=-\sum _{p\in {\mathcal {P}}}\sum _{\nu \geq 1}{\frac {\ln p}{p^{\nu s}}}

de sorte que l'on a, pour $Re(s)$ > 1, l'égalité :

D'(s)={\frac {\zeta '(s)}{\zeta (s)}}=-\sum _{n=1}^{\infty }{\frac {\Lambda (n)}{n^{s}}}

où les seules valeurs de $Λ$ (n) non nulles sont définies par $Λ$ (n) = $ln$ p lorsque n = p^m, p étant premier et m entier non nul. Il s'agit de la fonction de von Mangoldt. La définition de la série D se réécrit alors

D(s)=\sum _{n=2}^{\infty }{\frac {\Lambda (n)}{n^{s}\ln n}}.

Enfin en prenant le module de $e D (s) = ζ(s)$ on obtient $e Re(D (s)) = |ζ(s)|$ puis, prenant le logarithme réel on déduit

{\text{Re}}{\Big (}D(s){\Big )}=\ln |\zeta (s)|.

Convergence des séries de Dirichlet de $ln ζ$ , $1 / ζ$ et $ζ' / ζ$ sur la droite Re(s) = 1

Pour les séries de Dirichlet de $ln ζ$ et $1 / ζ$ ,

\ln \zeta (s)=\sum _{n=2}^{\infty }{\frac {\Lambda (n)}{n^{s}\ln n}}.

{\frac {1}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}

, où $μ$ est la fonction de Möbius,

l'application de la deuxième formule de Perron montre qu'elles convergent sur l'axe $Re(s) = 1$ en dehors de $s = 1$ , tandis que la série de Dirichlet de $ζ' / ζ$

{\frac {\zeta '(s)}{\zeta (s)}}=-\sum _{n=1}^{\infty }{\frac {\Lambda (n)}{n^{s}}}

diverge en tout point de l'axe 1.

Extension de $ln ζ$ à Re(s) ≤ 1

Pour les complexes s autres que 1 tels que $Re(s)$ ≤ 1, la définition du logarithme de $ζ(s)$ est plus délicate. La fonction $ζ$ ayant une infinité de zéros, $ln ζ$ admet une infinité de points de branchement. Dans les calculs, on pratique alors des coupures de la manière suivante. Une première coupure est pratiquée entre –2 et 1 (qui est aussi un point de branchement bien que $ζ$ ne s'y annule pas). Pour les zéros triviaux, une coupure est pratiquée sur les intervalles [–4n – 4, –4n – 6[ pour tout n ≥ 0. Pour les autres zéros, encore hypothétiques, de la forme $β + iγ$ avec $β$ ∈ ]0, 1[, ils sont répartis symétriquement par rapport à l'axe $Re(s)$ = $1 / 2$ . On pratique donc également une coupure parallèle à l'axe réel en reliant les deux zéros symétriques par rapport à l'axe $Re(s)$ = $1 / 2$ . Pour les zéros de l'axe $Re(s)$ = $1 / 2$ , la coupure pratiquée relie le point à l'infini au zéro considéré par une ligne parallèle à l'axe réel. Ce faisant, la fonction $ln ζ$ est alors uniforme sur le domaine coupé.

Le choix effectué donne

{\text{Re}}{\Big (}\ln \zeta (s){\Big )}=\ln |\zeta (s)|.

Représentation de 1/ζ et fonction M de Mertens

La fonction $1 / ζ$ est étudiée conjointement avec la fonction $ζ$ . On a une représentation par une série de Dirichlet sous la formule vue plus haut :

{\frac {1}{\zeta (s)}}=\sum _{1}^{\infty }{\frac {\mu (n)}{n^{s}}}.

On peut en déduire[24] que pour tout entier k > 1, la probabilité pour que k entiers > 0 pris au hasard soient premiers entre eux est égale à 1/ $ζ$ (k), ce qu'on pouvait « prévoir informellement » à partir du produit eulérien mentionné au § « Liens avec les nombres premiers ».

L'application de la formule sommatoire d'Abel donne également

\sum _{1}^{\infty }{\frac {\mu (n)}{n^{s}}}=s\int _{1}^{\infty }{{\frac {M(u)}{u^{1+s}}}\mathrm {d} u}

où $M$ est la fonction sommatoire de (la fonction de) Möbius : $M(u)=\sum _{n\leq u}^{\ }{\mu (n)}$ .

La formule intégrale est valable pour $Re(s)$ > 1. L'hypothèse de Riemann conjecture que l'intégrale converge et que la relation reste vraie pour $Re(s)$ > $1 / 2$ (s ≠ 1). On sait qu'elle est également valable pour s = 1 + $i$ t avec t ≠ 0.

La théorie de la fonction $M$ est très obscure et cela probablement pour longtemps. On sait démontrer l'estimation suivante[25] :

M(u)=O(u\mathrm {e} ^{-a(\ln u)^{3/5}(\ln \ln u)^{-1/5}}),

dont la preuve dépend directement de la plus grande région connue dans la bande critique qui ne contient pas de zéro de la fonction zêta (voir plus bas).

L'hypothèse de Riemann est équivalente à l'affirmation suivante : pour tout ε > 0,

M(x)=O(x^{{\frac {1}{2}}+\varepsilon }).

Une autre conjecture est l'hypothèse de Mertens généralisée qui affirme que : $M(x)=O({\sqrt {x}})$ , c'est-à-dire que

|M(x)|\leq A{\sqrt {x}}.

pour une certaine constante A (voir plus bas). Elle entraîne la conjecture de Riemann.

Inégalités

Inégalité de Mertens

En 1898, Franz Mertens démontre[26]

\zeta ^{3}(\sigma )|\zeta (\sigma +{\rm {i}}t)|^{4}|\zeta (\sigma +2{\rm {i}}t)|\geq 1,\quad {\rm {pour}}\quad s=\sigma +{\rm {i}}t,\quad {\text{Re}}(s)>1.

Cette inégalité permet de démontrer que la fonction ζ(s) ne s'annule pas sur $Re(s)$ = 1, ce qui est une étape cruciale dans la démonstration du théorème des nombres premiers.

Inégalité de Laforgia et Natalini

L'inégalité de Laforgia et Natalini est la suivante[27] :

{\frac {(s+1)\zeta (s)}{s\zeta (s+1)}}>{\frac {\zeta (s+1)}{\zeta (s+2)}},

pour s > 1.

Inégalité de Ahsan, Lam-Estrada, Lopez-Bonilla et Lopez-Vazquez

Ahsan, Lam-Estrada, Lopez-Bonilla et Lopez-Vazquez ont démontré l'inégalité suivante[28] :

\zeta (s)\zeta (s+2)>(\zeta (s+1))^{2},

pour s > 1.

Elle implique l'inégalité de Laforgia et Natalini.

Estimation de la fonction dans les diverses régions du plan

Le module de la fonction

(u, t) \mapsto ζ(u + i t)

de Riemann pour

0 \leq u \leq 3

0,1 \leq t \leq 200

. On notera la pointe due au pôle en 1 et la très grande irrégularité du module.

Presque périodicité

La fonction $ζ$ est presque périodique au sens de Bohr dans la région $Re(s)$ > 1. Il en est de même de ses dérivées. La fonction $1/ζ$ est également presque périodique sur $Re(s)$ > 1 ainsi que ses dérivées. Par contre sur l'axe $Re(s)$ = 1, la presque périodicité de Bohr cède sa place à la presque périodicité B2, au sens de Besicovitch.

La presque périodicité au sens de Bohr, sur la ligne $Re(s)$ = σ₀, signifie qu'à ε près, la fonction se répète indéfiniment dans des intervalles de longueur L(σ₀, ε). Évidemment, plus ε est petit, plus L(σ₀, ε) est grand.

Estimations dans la région $Re(s)$ > 1

Dans le demi-plan $Re(s)$ = σ > σ₀ > 1 la fonction $ζ(s)$ est bornée. Ses valeurs satisfont à l'inégalité

{\frac {\zeta (2\sigma )}{\zeta (\sigma )}}\leq |\zeta (\sigma +\mathrm {i} t)|\leq \zeta (\sigma ).

Elle n'a donc aucun zéro dans le demi-plan $Re(s)$ = σ > 1.

Ces deux bornes sont les meilleures possibles : on montre, pour chaque valeur σ, qu'il existe une suite de $t$ tendant vers l'infini ayant cette valeur pour limite de la suite $ζ(σ + i t)$ .

Franz Mertens démontra que pour σ > 1, on a

\zeta ^{3}(\sigma )|\zeta (\sigma +\mathrm {i} t)|^{4}|\zeta (\sigma +2\mathrm {i} t)|\geq 1.

Une estimation, souvent utile, est donnée par la formule suivante pour les valeurs réelles de s supérieures à 1

\zeta (\sigma )\leq {\frac {\sigma }{\sigma -1}}.

Elle résulte de la formule issue de la formule sommatoire d'Abel déjà donnée en remarquant que l'intégrale est toujours positive et affectée du signe –.

Estimations sur $Re(s)$ = 1

La fonction $ζ$ est presque périodique sur le demi plan $Re(s)$ > 1. Elle y est donc bornée sur tout demi-plan fermé strictement inclus. La présence du pôle en 1 empêche toute extension de la presque périodicité au sens de Bohr à un demi-plan plus vaste. Il est donc important de connaître le comportement de la fonction sur l'axe $Re(s)$ = 1.

La méthode de Vinogradov-Korobov sur les majorations des sommes d'exponentielles permet de montrer que l'on a, pour tout $t$ , l'inégalité

|\zeta (1+\mathrm {i} t)|<C_{1}(\ln |t|)^{2/3}.\,

On connaît, sans aucune hypothèse, une minoration de l'ordre des fonctions $ζ(1 + i t)$ et $1/ζ(1 + i t)$ . On a en effet ( $γ$ = 0,577… est la constante d'Euler-Mascheroni)

\limsup _{t\rightarrow \infty }{\frac {|\zeta (1+\mathrm {i} t)|}{\ln \ln t}}\geq \mathrm {e} ^{\gamma }

\limsup _{t\rightarrow \infty }{\frac {\left|{\frac {1}{\zeta (1+\mathrm {i} t)}}\right|}{\ln \ln t}}\geq {\frac {6}{\pi ^{2}}}\mathrm {e} ^{\gamma }.

La fonction n'est donc pas bornée sur l'axe $Re(s)$ = 1, même en dehors du voisinage de 1.

On connaît, sous l'hypothèse de Riemann, l'ordre exact des fonctions $ζ(1 + i t)$ et $1/ζ(1 + i t)$ . On a en effet

\mathrm {e} ^{\gamma }\leq \limsup _{t\rightarrow \infty }{\frac {|\zeta (1+\mathrm {i} t)|}{\ln \ln t}}\leq \mathrm {e} ^{2\gamma }

{\frac {6}{\pi ^{2}}}\mathrm {e} ^{\gamma }\leq \limsup _{t\rightarrow \infty }{\frac {\left|{\frac {1}{\zeta (1+\mathrm {i} t)}}\right|}{\ln \ln t}}\leq {\frac {12}{\pi ^{2}}}\mathrm {e} ^{2\gamma }.

Estimations sur $Re(s)$ = 0

Utilisant la formule des compléments et la relation fonctionnelle, on trouve pour $t$ non nul

|\zeta (\mathrm {i} t)|={\sqrt {\frac {t}{\pi \operatorname {sh} (\pi t)}}}\operatorname {sh} \left({\frac {\pi |t|}{2}}\right)|\zeta (1+\mathrm {i} t)|

et de ce fait

|\zeta (\mathrm {i} t)|=O\left({\sqrt {|t|}}\ln ^{2/3}|t|\right).

Estimations dans la région $Re(s)$ < 0

L'application de l'équation fonctionnelle et de la formule de Stirling, et le comportement asymptotique de $sin(σ + i t)$ permet de montrer que

|\zeta (\sigma +\mathrm {i} t)|\ll \left({\frac {t}{2\pi }}\right)^{{\frac {1}{2}}-\sigma }

pour σ < 0.

Estimation dans la bande critique

On peut estimer, uniformément dans la bande critique, $ζ(s)$ par la formule

\zeta (\sigma +\mathrm {i} t)=\sum _{n\leq t}{\frac {1}{n^{\sigma +\mathrm {i} t}}}+O\left(|t|^{-\sigma }\right).

De la méthode de Vinogradov-Korobov on déduit la majoration suivante : il existe deux constantes $c$ et $C$ strictement positives telles que pour tout σ ∈ [ $1 / 2$ ; 1] et $t > 3$ , on ait

|\zeta (\sigma +\mathrm {i} t)|\leq C\;t^{c(1-\sigma )^{3/2}}(\ln t)^{2/3}.

Dans l'état actuel des connaissances, d'après Ford[29], on peut prendre $C$ = 76,2 et $c$ = 4,45. La relation fonctionnelle permet d'estimer le module dans la bande σ ∈ [0 ; $1 / 2$ ].

Le théorème de Valiron

Quand on regarde les applications arithmétiques de la fonction $ζ$ , on est frappé par l'usage quasi systématique des fonctions $1/ζ$ , $ζ'/ζ$ , ou $ln ζ$ mais la fonction $ζ$ elle-même apparaît rarement au numérateur. Comme la région importante est la bande critique 0 ≤ $Re(s)$ ≤ 1, il est important de pouvoir traverser cette bande. Or la présence éventuelle de zéros sur le chemin complique singulièrement les calculs et les estimations. Le résultat suivant sert essentiellement à majorer la fonction $1/ζ$ sur des chemins bien répartis.

Dans sa thèse soutenue en 1914, Georges Valiron a montré qu'il existait une infinité de valeurs de $t$ dans tout intervalle $[T, T + 1]$ pour lesquelles on avait la minoration

|\zeta (\sigma +\mathrm {i} t)|\geq t^{-\delta }.

pour un certain δ fixe strictement positif.

On ne connaît aucune valeur de δ qui convient. On sait seulement que 0 ≤ δ ≤ 1. Sous l'hypothèse de Riemann, on peut prendre δ aussi petit qu'on veut.

La relation fonctionnelle approchée

Comme indiqué dans la partie consacrée à l'estimation dans la bande critique, il est possible de calculer la fonction $ζ$ dans la bande critique en utilisant une somme partielle de la série de Dirichlet. La relation fonctionnelle se traduit alors dans une relation approchée reliant les séries de Dirichlet partielles pour les exposants s et 1 – s. C'est la relation fonctionnelle approchée :

Pour 0 < σ < 1 et $2π xy = t$ avec $x > h > 0$ , $y > h > 0$ , on a

\zeta (s)=\sum _{n\leq x}{\frac {1}{n^{s}}}+\chi (s)\sum _{n\leq y}{\frac {1}{n^{1-s}}}+O(x^{-\sigma }\ln |t|)+{\mathcal {O}}(|t|^{{\frac {1}{2}}-\sigma }y^{\sigma -1})

avec

\chi (s)={\frac {2^{s-1}\pi ^{s}}{\Gamma (s)}}\sec \left({\frac {1}{2}}s\pi \right).

On peut, avec elle, obtenir une première estimation de $|ζ(1 / 2 + i t)|$ , l'objectif étant de démontrer l'hypothèse de Lindelöf (voir plus loin).

La théorie de la fonction mu

On utilise ici les résultats vus plus haut dans la partie « Estimation de la fonction dans les diverses régions du plan ».

L'estimation de $ζ$ dans la partie $Re(s)$ < 0 montre que la fonction $t \mapsto ζ(σ + i t)$ est d'ordre fini : elle est majorée par une puissance de $t = Im(s)$ .

Dans la région $Re(s)$ > σ₀ > 1, la majoration est celle d'une constante.

Graphe de la fonction

μ

en fonction de σ. En noir, la partie connue. En jaune la partie supposée conformément à l'hypothèse de Lindelöf. En rouge la majoration par la convexité.

La théorie des séries de Dirichlet montre que dans la bande critique, la fonction est encore d'ordre fini sauf en s = 1. La question qui se pose alors est celle de l'estimation de cet exposant. On appelle traditionnellement $μ$ (σ) la borne inférieure des exposants $μ$ tels que $|ζ(σ + i t)| ≪ t μ$ .

Le théorème de Phragmén-Lindelöf[30] implique que la fonction $μ$ est une fonction convexe décroissante de σ.

On a de plus :

$μ$ (σ) = $1 / 2$ – σ pour σ < 0 et
$μ$ (σ) = 0 pour σ > 1.
La propriété de convexité impose, dans la bande critique, $μ$ (σ) ≤ $1 / 2$ – $σ / 2$

mais on ignore la valeur exacte de $μ$ (σ) pour 0 < σ < 1.

La convexité donne $μ$ ( $1 / 2$ ) ≤ $1 / 4$ = 0,25.

La relation fonctionnelle approchée (voir plus haut) donne : $μ$ ( $1 / 2$ ) ≤ $1 / 6$ < 0,16667.

On sait que $μ$ ( $1 / 2$ ) ≤ $32 / 205$ ≈ 0,156098 d'après M.N. Huxley[31].

Les zéros

Les zéros triviaux

Zéros triviaux de la fonction zêta.

Par la relation fonctionnelle, il apparaît que la fonction $ζ$ s'annule pour tous les entiers de la forme –2k, (k > 0) par suite du facteur $\sin \left({\frac {\pi s}{2}}\right)$ , mais pas en $s = 0$ par suite du facteur $Γ(1 - s)$ . Ces zéros sont appelés les zéros triviaux.

La relation fonctionnelle permet de plus de montrer que chacun de ces zéros est simple puisque la valeur de la dérivée en –2k est :

\zeta '(-2k)=(-1)^{k}{\frac {(2k)!\zeta (2k+1)}{2^{2k+1}\pi ^{2k}}}\neq 0.

Les zéros non triviaux

Double spirale traversant cinq fois l'origine du graphique

Trajectoire de

ζ(1 / 2 + i y)

pour y de 0 à 34.

Représentation en bleu de la partie réelle et en rouge de la partie imaginaire de la fonction

ζ(1 / 2 + i x)

sur l'intervalle [0, 100], où l'on voit clairement apparaître les premiers zéros non triviaux lorsque les deux courbes se croisent sur l'axe des abscisses.

Il existe d'autres zéros. On obtient de la relation fonctionnelle que la fonction $ζ$ admet une infinité de zéros dans la bande $Re(s)$ ∈ ]0, 1[. Pour cela, on remarque que la fonction

\xi (s)={\frac {1}{2}}s(s-1)\pi ^{-s/2}\Gamma (s/2)\zeta (s)

vérifie

\displaystyle \xi (s)=\xi (1-s).

On en déduit que la fonction

\Xi (s)=\xi \left({\frac {1}{2}}+\mathrm {i} s\right)

est paire. On montre que les deux fonctions $ξ$ et $Ξ$ sont deux fonctions entières d'ordre 1 et, comme $Ξ(s)$ est paire, la fonction $s \mapsto Ξ$ ( $\sqrt s$ ) est une fonction entière d'ordre $1 / 2$ : elle admet donc, d'après la théorie générale des fonctions entières, une infinité de zéros. Ces zéros se traduisent par une infinité de zéros de $ζ$ dans la bande $Re(s)$ ∈]0, 1[. On ignore pour l'instant si l'hypothèse de Riemann (voir plus bas), qui affirme que tous ces zéros sont de partie réelle $1 / 2$ , est vraie.

Premiers zéros sur la droite critique
± k	Partie imaginaire de ρ_k
1	± 14,134 725 141 734 693 790…
2	± 21,022 039 638 771 554 993…
3	± 25,010 857 580 145 688 763…
4	± 30,424 876 125 859 513 210…

Représentation sous forme de produit de facteurs primaires (produit de Hadamard)

D'après le théorème de factorisation de Hadamard pour une fonction méromorphe, toute fonction méromorphe s'écrit sous forme de produit de facteurs dits primaires dans lesquels apparaissent les zéros et les pôles de la fonction. La représentation sous cette forme pour $ζ$ prend la forme

\zeta (s)={\frac {\mathrm {e} ^{\left(\ln(2\pi )-1-{\frac {\gamma }{2}}\right)s}}{2(s-1)\Gamma (1+{\frac {s}{2}})}}\prod _{\rho }\left(1-{\frac {s}{\rho }}\right)\mathrm {e} ^{s/\rho }

où le produit s'effectue sur les zéros non-triviaux $ρ$ de $ζ$ et $γ$ est la constante d'Euler-Mascheroni.

Expressions de ζ'/ζ en fonction des zéros triviaux et non triviaux

Indépendamment de l'expression en fonction des facteurs primaires de Weierstrass, la valeur $ζ(s)$ peut se calculer en fonction des zéros non triviaux les plus proches du point $s = σ + i t$ . On démontre que seuls les zéros à une distance de $t$ inférieure à 1 interviennent vraiment. Le reste s'exprime dans la notation « de Landau » .

Il faut faire attention au fait que les expressions faisant intervenir une somme sur les zéros $ρ = β + iγ$ ne sont généralement pas commutativement convergentes et que l'ordre de sommation intervient : on somme symétriquement par rapport à $1 / 2$ . D'autre part, les zéros $ρ$ sont comptés autant de fois que leur multiplicité dans ces sommes.

La première expression intéressante, déduite du produit de Hadamard précédent, est :

{\frac {\zeta '(s)}{\zeta (s)}}=\ln 2\pi -{\frac {1}{2}}\gamma -1-{\frac {1}{s-1}}-{\frac {1}{2}}{\frac {\Gamma '({\frac {1}{2}}s+1)}{\Gamma ({\frac {1}{2}}s+1)}}+\sum _{\rho }{\Big (}{\frac {1}{s-\rho }}+{\frac {1}{\rho }}{\Big )}.

La somme s'effectue sur les zéros non-triviaux $ρ$ de $ζ$ et $γ$ est la constante d'Euler-Mascheroni.

On en déduit :

{\frac {\zeta '(s)}{\zeta (s)}}=\sum _{\rho }{\Big (}{\frac {1}{s-\rho }}+{\frac {1}{\rho }}{\Big )}+O(\ln |t|).

Cette formule montre alors, sans l'hypothèse de Riemann,

{\frac {\zeta '(s)}{\zeta (s)}}=\sum _{|t-\gamma |\leq 1}{\frac {1}{s-\rho }}+O(\ln |t|).

Avec l'hypothèse de Riemann, la sommation peut être considérablement diminuée. On a

{\frac {\zeta '(s)}{\zeta (s)}}=\sum _{|t-\gamma |\leq {\frac {1}{\ln \ln t}}}{\frac {1}{s-\rho }}+O(\ln |t|).

La bande critique et l'hypothèse de Riemann

La série des points blancs marque les points où la fonction zêta s'annule.

On appelle bande critique la bande 0 < $Re(s)$ < 1. Il existe donc une infinité de zéros dans la bande critique mais, actuellement, on ne sait pas exactement où. L'hypothèse de Riemann affirme qu'ils sont tous de partie réelle $1 / 2$ . On a vérifié numériquement sur plus de 1 500 000 000 zéros que leur partie réelle était bien $1 / 2$ [note 10].

Il a été démontré que l'axe $Re(s)$ = $1 / 2$ en avait une infinité, dont les 2/5 au moins sont simples. On sait également que la proportion des zéros de la forme $β + iγ$ en dehors de l'axe $Re(s)$ = $1 / 2$ et tels que $|γ| < T$ tend vers 0 quand $T$ tend vers l'infini, cette proportion décroissant également à mesure que $β$ s'écarte de $1 / 2$ .

On appelle traditionnellement N(T) le nombre de zéros de la fonction $ζ$ de Riemann dans le rectangle vertical décrit par sa diagonale $]0, 1 + i T]$ . On note aussi N₀(T) le nombre de zéros se trouvant sur le segment $[1 / 2, 1 / 2 + i T]$ . On a alors les estimations suivantes :

N(T)={\frac {T}{2\pi }}\ln \left({\frac {T}{2\pi \mathrm {e} }}\right)+O\left(\ln T\right).

Démonstration

On part de

\xi (s)={\frac {1}{2}}s(s-1)\pi ^{-s/2}\Gamma (s/2)\zeta (s),

pour laquelle on sait qu'on a, d'après la relation fonctionnelle :

ξ

(s) =

ξ

(1 – s).

Le nombre de zéros de $ξ$ (s) est le même que celui de $ζ(s)$ dans le rectangle défini par les sommets opposés 0 et $1 + i T$ , soit N(T).

En effet, la fonction

{\frac {\xi (s)}{\zeta (s)}}={\frac {1}{2}}s(s-1)\pi ^{-s/2}\Gamma (s/2)

ne s'annule pas dans la bande verticale ]0, 1[, celle-ci n'ayant que les zéros réels s = 0 et s = 1 (elle admet une infinité de pôles réels pour les demi-entiers négatifs par la fonction gamma.)

Si T n'est pas l'ordonnée d'un zéro, $2π N (T)$ est égal à la variation de l'argument de $ξ$ (s) le long du rectangle, conformément au principe de l'argument.

Or, $ξ$ (s) est réelle pour t = 0 et également pour σ = $1 / 2$ , de sorte que la variation totale autour du rectangle est 2 fois la variation autour de la moitié en partant de s = 2. Donc $π N (T)$ est égal à la variation d'argument entre $2$ et $2 + i T$ et de $2 + i T$ à $1 / 2 + i T$ le long des droites.

D'où

\pi N(T)=\int _{2}^{2+\mathrm {i} T}+\int _{2+\mathrm {i} T}^{{\frac {1}{2}}+\mathrm {i} T}{\frac {\xi '(s)}{\xi (s)}}~\mathrm {d} s.

Comme

{\frac {\xi '(s)}{\xi (s)}}={\frac {1}{s}}+{\frac {1}{s-1}}-{\frac {1}{2}}\ln \pi +{\frac {1}{2}}{\frac {\Gamma '(s/2)}{\Gamma (s/2)}}+{\frac {1}{2}}{\frac {\zeta '(s)}{\zeta (s)}}

on a en utilisant la formule de Stirling complexe,

N(T)={\frac {T}{2\pi }}\ln {\frac {T}{2\pi }}-{\frac {T}{2\pi }}+{\frac {7}{8}}+O(1/T)+{\frac {1}{\pi }}{\text{Im}}\left(\int _{{\frac {1}{2}}+\mathrm {i} T}^{2+\mathrm {i} T}{\frac {\zeta '(s)}{\zeta (s)}}ds\right)

car, la partie réelle de

ζ(s)

ne s'annulant pas sur l'axe σ = 2 puisque

{\text{Re}}(\zeta (2+\mathrm {i} t))\geq 1-\sum _{n=2}^{\infty }n^{-2}>0,

la variation de l'argument de

ζ(s)

entre 2 et

2 + i T

est inférieure à

π

/2.

Il reste à montrer que le dernier terme est $O (ln T)$ .

Si $Re$ (ζ(s)) s'annule q fois entre $2 + i T$ et $1 / 2 + i T$ , cet intervalle est divisé en q + 1 parties à travers lesquelles $Re$ (ζ(s)) ne prend qu'un signe, soit + soit –. Donc dans chaque partie la variation de l'argument de ζ(s) n'excède pas $π$ . et ainsi la variation totale de l'argument est inférieure à (q + 3/2) $π$ . Il reste à évaluer q.

Or q est le nombre de zéros de

f(z)={\frac {1}{2}}\left(\zeta (z+\mathrm {i} T)+\zeta (z-\mathrm {i} T)\right)\quad {\text{pour}}\quad {\text{Im}}(z)=0{\text{ et }}{\frac {1}{2}}\leq {\text{Re}}(z)\leq 2,

et donc q est nécessairement inférieur au nombre de zéros de

f (z)

dans

| z -2| \leq 3 / 2

. On applique alors la formule de Jensen :

« Soit $f$ une fonction analytique dans le disque $| z | \leq r$ contenant les zéros $a 1, a 2, \dots , a n$ . Alors
$\ln |f(0)|=-\sum _{k=1}^{n}\ln \left({\frac {r}{|a_{k}|}}\right)+{\frac {1}{2\pi }}\int _{0}^{2\pi }\ln |f(r\mathrm {e} ^{\mathrm {i} \theta })|~\mathrm {d} \theta .$ »

qui donne

q<A\left(\int _{0}^{2\pi }\ln |f(2+r\mathrm {e} ^{\mathrm {i} u})|~\mathrm {d} u-2\pi \ln |f(2)|\right)\quad \mathrm {o{\grave {u}}} \quad 3/2<r<2

et parce que

ξ

(s) = O(t^{1 – σ}), le membre de droite est inférieur à

A ln T

D'où le résultat annoncé.

Ces estimations permettent de donner une estimation asymptotique pour le zéro de rang $n$ , $β n + iγ n$ sous la forme

|\gamma _{n}|\approx {\frac {2\pi n}{\ln n}}.

Cette formule montre d'une part que l'ordre $m (ρ)$ de chaque zéro $ρ$ est majoré par

m(\rho )\leq C\ln |\rho |

et d'autre part que la distance entre deux zéros tend vers 0. On a en effet

|\gamma _{n+1}-\gamma _{n}|=O\left(1/\ln n\right).

Pour les zéros de la droite critique, on sait qu'il existe une constante C telle que, pour tout T ≥ 2 on a

N_{0}(T)\geq CT\ln T\geq CN(T).

On ne connaît pas la valeur exacte de la constante C mais Conrey a démontré en 1989 que

\liminf _{T\to +\infty }{\frac {N_{0}(T)}{N(T)}}\geq 0,4077.

Autrement dit, plus de deux cinquièmes des zéros de $ζ$ sont sur la droite critique $Re(s)$ = $1 / 2$ .

La fonction S(T)

À partir de la fonction entière $ξ$ , qui satisfait $\xi (s)=s(s-1)\pi ^{-s/2}\Gamma (s/2)\zeta (s)$ et $\xi (s)=\xi (1-s)$ et dont les zéros sont les zéros non triviaux, on trouve avec le principe de l'argument[32]

N(T)={\frac {1}{2\mathrm {i} \pi }}\int _{\begin{array}{l}[2,2+\mathrm {i} T,\\-1+\mathrm {i} T,\\-1,2]\end{array}}{\frac {\xi '(s)}{\xi (s)}}\,\mathrm {d} s={\frac {1}{i\pi }}\int _{2}^{2+\mathrm {i} T}+\int _{2+\mathrm {i} T}^{1/2+\mathrm {i} T}{\frac {\xi '(s)}{\xi (s)}}\,\mathrm {d} s=1+{\frac {1}{\pi }}\arg {\Big (}\pi ^{-\mathrm {i} T/2}\Gamma (1/4+\mathrm {i} T/2){\Big )}+S(T)

où $S(T)={\frac {1}{\pi }}\arg {\Big (}\zeta \left({\frac {1}{2}}+\mathrm {i} T\right){\Big )}$ , les arguments étant définis par variation continue sur le chemin $[2,2+\mathrm {i} T,1/2+\mathrm {i} T]$ et en partant de la valeur $0$ .

La formule de Stirling complexe donne alors

N(T)={\frac {T}{2\pi }}\ln {\frac {T}{2\pi \mathrm {e} }}+{\frac {7}{8}}+S(T)+O\left(1/T\right).

On connaît relativement peu de chose sur $S (T)$ sans aucune hypothèse. On a l'estimation

S(T)=O\left(\ln T\right)

déjà ancienne et qu'on n'arrive pas à améliorer.

Sous l'hypothèse de Riemann, on a

S(T)=O\left(\ln T/\ln \ln T\right).

Dans les recherches sur $S (T)$ , on a réussi à avoir quelques précisions supplémentaires sur le comportement de $S (T)$ qui reste mystérieux :

\int _{0}^{T}S(u)\mathrm {d} u=O\left(\ln T\right)

dont on déduit que la moyenne de $S (T)$ est égale à zéro.

Cependant Selberg a montré que $S (T)$ était minoré par une quantité tendant vers l'infini pour une infinité de valeurs de T. Sur ces valeurs de T, on a

S(T)>A(\ln T)^{1/3}(\ln \ln T)^{-7/3}.

Selberg a également montré que

\int _{0}^{T}S^{2}(u)\mathrm {d} u={\frac {1}{2\pi ^{2}}}T\ln \ln T(1+o(1))

qui montre que la moyenne de $S 2 (T)$ sur [0, T] est $(1 / 2π 2) ln ln T$ .

Edward Charles Titchmarsh a montré d'autre part que $S (T)$ changeait de signes une infinité de fois.

La région sans zéro

Région (en bleu) sans zéro de la fonction zêta.

La plus grande région connue qui ne contient aucun zéro de la fonction $ζ$ est donnée asymptotiquement par la formule suivante[33] :

{\text{Re}}(s)>1-{\frac {c}{(\ln t)^{2/3}(\ln \ln t)^{1/3}}}.

Les grandes conjectures

L'hypothèse de Riemann

Elle exprime que tous les zéros qui se trouvent dans la bande critique sont de partie réelle égale à $1 / 2$ . Elle ne dit rien sur la multiplicité des zéros.

Cette hypothèse, formulée dès 1859 par Bernhard Riemann, a de très grandes conséquences dans le comportement asymptotique de nombreuses fonctions arithmétiques qui se trouvent liées à $ζ$ , ainsi que sur l'étude de la répartition des nombres premiers.

Les conséquences sur le comportement de la fonction $ζ$ sont nombreuses. On en donne quelques-unes dans ce qui suit.

Cette hypothèse reste pour l'instant non démontrée, mais tous les zéros calculés jusqu'ici par ordinateur la vérifient.

Conséquences de l'hypothèse de Riemann sur la croissance de la fonction zêta

L'hypothèse de Riemann entraine que l'on a δ = 0 dans le théorème de Valiron. En fait, on montre bien mieux sous l'hypothèse de Riemann car la fonction $ln ζ$ est alors analytique régulière dans le demi-plan $Re(s)$ > $1 / 2$ .

Sous l'hypothèse de Riemann, on a, uniformément pour tout σ tel que $1 / 2$ < σ₀ ≤ σ ≤ 1 :

\ln \zeta (\sigma +\mathrm {i} t)=O{\Big (}(\ln t)^{2-2\sigma +\epsilon }{\Big )}

et même plus précisément, si l'on suppose ${\frac {1}{2}}+{\frac {1}{\ln \ln t}}\leq \sigma \leq 1$ , on a

\ln \zeta (\sigma +\mathrm {i} t)=O{\Big (}\ln \ln t(\ln t)^{2-2\sigma }{\Big )}.

De cela on déduit, pour tout σ > $1 / 2$ , car l'exposant dans la formule précédente est inférieur à 0,

\zeta (\sigma +\mathrm {i} t)=O\left(t^{\epsilon }\right)\;{\text{ et }}\;{\frac {1}{\zeta (\sigma +\mathrm {i} t)}}=O\left(t^{\epsilon }\right).

Autrement dit, l'hypothèse de Riemann implique l'hypothèse de Lindelöf (voir plus bas).

Il en résulte également l'estimation

\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{1}^{T}{\frac {\mathrm {d} t}{|\zeta (\sigma +\mathrm {i} t)|^{2}}}={\frac {\zeta (2\sigma )}{\zeta (4\sigma )}}.

On peut développer, sous l'hypothèse de Riemann, une théorie voisine de celle de la fonction $\mu (\sigma )$ mais pour la fonction $ζ'$ (voir #La théorie de la fonction mu).

En supposant σ > $1 / 2$ et appelant $ν (σ)$ le plus petit exposant $α$ pour lequel on a $\ln \zeta (\sigma +\mathrm {i} t)=O{\Big (}(\ln t)^{\alpha }{\Big )}$ , on montre que $ν (σ)$ est une fonction convexe décroissante de σ satisfaisant aux inégalités 1 – σ ≤ $ν (σ)$ ≤ 2(1 – σ). On montre aussi que la fonction $ν (σ)$ de $\displaystyle {\frac {\zeta '(\sigma +\mathrm {i} t)}{\zeta (\sigma +\mathrm {i} t)}}$ est la même fonction $ν$ (σ) que celle de $ln ζ(σ + i t)$ . Mais on ignore encore la valeur de $ν (σ)$ pour tout σ ∈ ] $1 / 2$ , 1[. Pour σ ≥ 1, $ν (σ) = 0$ .

L'hypothèse de Riemann et les zéros de la dérivée $ζ'$

La question de la position des zéros de la dérivée $ζ'$ est liée également à l'hypothèse de Riemann. Littlewood a démontré le théorème

« Ou bien la fonction $ζ$ ou bien la fonction $ζ'$ a une infinité de zéros dans la bande 1 – δ < σ < 1, δ étant une quantité positive arbitrairement petite. »

et Speiser a démontré que

« L'hypothèse de Riemann est équivalente à l'absence de zéro non trivial de la dérivée $ζ'$ dans le demi-plan σ < $1 / 2$ . »

De même, Yıldırım[34] a démontré que

« L'hypothèse de Riemann implique que $ζ''$ (s) et $ζ'''$ (s) ne s'annulent pas dans la bande 0 < $Re(s)$ < $1 / 2$ . »

L'hypothèse de Lindelöf et l'hypothèse de densité

La conjecture de Lindelöf est l'assertion que pour tout ε > 0

\left|\zeta \left({\frac {1}{2}}+\mathrm {i} t\right)\right|=O(t^{\varepsilon })\ (t\rightarrow \infty ).

Cela a entre autres pour conséquence immédiate que $μ$ ( $1 / 2$ ) = 0. On connaît alors la valeur exacte de la fonction $μ$ . Le graphe de $μ$ est composé des deux seules demi-droites indiquées, qui se rejoignent en σ = $1 / 2$ à la valeur 0.

Cette hypothèse a de nombreuses formulations équivalentes intéressantes. En voici deux :

Pour tout k ≥ 1, on a ${\frac {1}{T}}\int _{1}^{T}{\left|\zeta \left({\frac {1}{2}}+\mathrm {i} u\right)\right|^{2k}\mathrm {d} u}=O(T^{\epsilon })$
Pour tout k ≥ 1, et tout σ > $1 / 2$ on a ${\frac {1}{T}}\int _{1}^{T}{|\zeta (\sigma +\mathrm {i} u)|^{2k}\mathrm {d} u}=O(T^{\epsilon })$

L'hypothèse de Lindelöf a pour conséquence la raréfaction des zéros à mesure qu'on s'écarte de l'axe σ = $1 / 2$ . Cette dernière propriété est appelée hypothèse de densité quand on la considère par elle-même. Appelant N(σ, T) le nombre de zéros sur la droite $Re(s)$ = σ et dont la partie imaginaire reste inférieure ou égale à T, on a, sous l'hypothèse de Lindelöf,

N(\sigma ,T)\leq O(T^{2(1-\sigma )+\epsilon }).

Par contre, on ignore si l'hypothèse de Lindelöf, qui a comme on vient de voir une influence sur la position des zéros, implique ou non l'hypothèse de Riemann.

Les hypothèses de Mertens

Sur une table numérique allant jusqu'à 10 000 de la fonction de Mertens $M (x)$ , Mertens en 1897 conjectura que l'on a

|M(x)|\leq {\sqrt {x}}.

Cette conjecture a été réfutée en 1985 par Odlyzko et te Riele. Cependant, la conjecture généralisée de Mertens, qui s'exprime sous la forme

|M(x)|\leq A{\sqrt {x}}

pour un certain $A > 1$ , n'est pas réfutée.

Une troisième formulation est la forme affaiblie :

\int _{1}^{x}{{\frac {M^{2}(u)}{u^{2}}}\mathrm {d} u}=O(\ln x).

La forme généralisée implique la forme affaiblie. La forme affaiblie implique l'hypothèse de Riemann (et donc l'hypothèse de Lindelöf) et la simplicité des zéros.

La conjecture des paires corrélées

La conjecture (faible) des paires corrélées exprime que, pour un nombre $α > 0$ ,

\sum _{0<\gamma ,\gamma '<T,0<\gamma -\gamma '<{\frac {2\pi \alpha }{\ln T}}}1={\frac {T\ln T}{2\pi }}(1+o(1))\int _{0}^{\alpha }1-\left({\frac {\sin(\pi u)}{\pi u}}\right)^{2}\mathrm {d} u.

Cette dernière conjecture fait le lien avec la théorie des matrices aléatoires.

La conjecture de Hilbert-Polya

Hilbert et Polya ont suggéré que la conjecture de Riemann serait démontrée si l'on pouvait trouver un opérateur hermitien $Ĥ$ dont les valeurs propres (nécessairement réelles) soient exactement les parties imaginaires $E k$ des zéros non triviaux :

{\hat {H}}\ \psi _{k}\ =\ E_{k}\ \psi _{k}.

Un tel opérateur hermitien n'a pas encore été trouvé explicitement à ce jour. Néanmoins, cette équation aux valeurs propres suggère un lien avec un problème de mécanique quantique non relativiste qui est précisé dans le paragraphe suivant.

Propriétés statistiques des zéros non triviaux et chaos quantique

Les propriétés statistiques des zéros non triviaux de la fonction $ζ$ ressemblent asymptotiquement à celles des valeurs propres de matrices aléatoires de l'ensemble gaussien unitaire pour les systèmes non-invariants par renversement du temps (GUE). Cette conjecture est basée sur de nombreux résultats numériques, et fortement supportée par un théorème rigoureux de Montgomery[35]. Ceci a conduit le physicien théoricien Michael Berry à conjecturer que les parties imaginaires $E k$ des zéros non triviaux pouvaient s'interpréter comme les valeurs propres d'un opérateur hamiltonien décrivant un système quantique non relativiste qui serait classiquement chaotique, et dont les orbites classiques ne possèdent pas la symétrie de renversement du temps[36] - [37] - [38]. Mieux, un opérateur hamiltonien semblant posséder les bonnes propriétés a été exhibé par Berry et Jonathan Keating en 1999[39] - [40].

Les propriétés statistiques des zéros non triviaux continuent d'être l'objet d'intenses recherches, tant numériques qu'analytiques, ainsi que d'interprétations probabilistes[41] - [42].

Le problème des moments

Malgré quelques progrès, on n'a pas réussi à résoudre la question de l'ordre de $ζ$ dans la bande critique. Le problème de l'ordre moyen est lui, partiellement résolu. Il prend la forme de l'estimation de l'expression

\int _{1}^{T}|\zeta (\sigma +\mathrm {i} t)|^{2}\mathrm {d} t.

Cette estimation est donnée par un théorème général sur les séries de Dirichlet :

« Soient $f(s)=\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}$ et $g(s)=\sum _{n=1}^{\infty }{\frac {b_{n}}{n^{s}}}$ deux séries de Dirichlet absolument convergentes, la première pour $Re(s)$ > σ₀ et la seconde pour $Re(s)$ > σ₁.

Alors, pour α > σ₀ et β > σ₁, on a
$\lim _{T\rightarrow \infty }{\frac {1}{2T}}\int _{-T}^{T}f(\alpha +\mathrm {i} t)g(\beta -\mathrm {i} t)\mathrm {d} t=\sum _{n=1}^{\infty }{\frac {a_{n}b_{n}}{n^{\alpha +\beta }}}.$
»

En l'appliquant à la fonction $ζ$ , on trouve immédiatement, pour σ > 1

\lim _{T\rightarrow \infty }{\frac {1}{2T}}\int _{-T}^{T}|\zeta (\sigma +\mathrm {i} t)|^{2}\mathrm {d} t=\zeta (2\sigma )

\lim _{T\rightarrow \infty }{\frac {1}{2T}}\int _{-T}^{T}|\zeta (\sigma +\mathrm {i} t)|^{4}\mathrm {d} t={\frac {\zeta ^{4}(2\sigma )}{\zeta (4\sigma )}}.

On a donc cherché à étendre ces formules pour σ ≤ 1.

Le problème général des moments est donc l'évaluation des intégrales dépendantes de k, pour σ ≥ $1 / 2$

\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{1}^{T}|\zeta (\sigma +\mathrm {i} t)|^{2k}\mathrm {d} t.

Les résultats, désormais classiques, sont les suivants :

Pour le moment d'ordre 2 en σ = $1 / 2$ $\int _{0}^{T}\left|\zeta \left({\frac {1}{2}}+\mathrm {i} t\right)\right|^{2}\mathrm {d} t=T\ln T+(2\gamma -1-\ln 2\pi )T+O{\Big (}{\sqrt {T}}\ln T{\Big )}.$
Pour le moment d'ordre 2 en σ > $1 / 2$ $\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{1}^{T}|\zeta (\sigma +\mathrm {i} t)|^{2}\mathrm {d} t=\zeta (2\sigma ).$
Pour le moment d'ordre 4 en σ = $1 / 2$ $\int _{1}^{T}\left|\zeta \left({\frac {1}{2}}+\mathrm {i} t\right)\right|^{4}\mathrm {d} t={\frac {1}{2\pi ^{2}}}T(\ln T)^{4}+O{\Big (}T(\ln T)^{3}{\Big )}.$
Pour le moment d'ordre 4 en σ > $1 / 2$ $\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{1}^{T}|\zeta (\sigma +\mathrm {i} t)|^{4}\mathrm {d} t={\frac {\zeta ^{4}(2\sigma )}{\zeta (4\sigma )}}.$

Carlson a montré que, si l'on appelle σ_k la borne inférieure des σ pour lesquels on a $\lim _{T\rightarrow \infty }{\frac {1}{T}}\int _{1}^{T}|\zeta (\sigma +\mathrm {i} t)|^{2k}\mathrm {d} t=O(1)$ , alors

\sigma _{k}\leq \max {\Big (}1-{\frac {1-\alpha }{1+\mu _{k}(\alpha )}},{\frac {1}{2}},\alpha {\Big )}

pour $0 < α < 1$ , la quantité $μ k (α)$ étant l'équivalent de la fonction $μ$ de $ζ$ pour la fonction $ζ k$ .

Les moments d'ordre supérieur à 4 font encore l'objet d'intenses recherches. On sait qu'il existe une constante $C (k)$ telle que

\int _{0}^{T}\left|\zeta \left({\frac {1}{2}}+\mathrm {i} t\right)\right|^{2k}\mathrm {d} t\ll T^{(k+2)/4}(\ln T)^{C(k)}

pour 2 ≤ k ≤ 6 et on conjecture qu'il en est ainsi pour les k supérieurs à 6, en particulier 8.

L'importance du problème des moments est liée à l'hypothèse de Lindelöf (voir plus haut).

Applications diverses

Régularisation Zêta

Par l'intermédiaire de la fonction $ζ$ de Riemann, on a développé une méthode de régularisation des suites divergentes qui a trouvé des applications en physique, notamment dans l'effet Casimir.

Développement en série entière de ln Γ(1+t)

Une formule due à Euler donne pour $| t | < 1$

\ln \Gamma (1+t)=-\gamma t+\sum _{n=2}^{\infty }{\frac {(-1)^{n}\zeta (n)}{n}}t^{n}.

Elle permet à Euler d'écrire[43]

\gamma =\sum _{n=2}^{\infty }{\frac {(-1)^{n}\zeta (n)}{n}}.

Legendre[44] écrit la formule d'Euler sous la forme plus commode numériquement

\ln \Gamma (1+t)={\frac {1}{2}}\ln {\frac {\pi t}{\sin \pi t}}+{\frac {1}{2}}\ln {\frac {1-t}{1+t}}+(1-\gamma )t+\sum _{n=1}^{\infty }{\frac {1-\zeta (2n+1)}{2n+1}}t^{n}.

Suites de Farey et hypothèse de Riemann

Ces suites peuvent être utilisées pour obtenir des formules équivalentes à l'hypothèse de Riemann.

Fonction de comptage des nombres premiers et théorème des nombres premiers

La fonction de comptage des nombres premiers est définie par

\pi (x)=\sum _{p\in {\mathcal {P}},p\leq x}1.

La non-annulation de la fonction $ζ$ sur $Re(s)$ = 1 a pour conséquence la véracité de la conjecture de Legendre-Gauss :

\pi (x)\sim \int _{2}^{x}{\frac {\mathrm {d} u}{\ln u}}.

La région sans zéro permet ensuite de majorer le reste :

\pi (x)=\int _{2}^{x}{\frac {\mathrm {d} u}{\ln u}}+O{\Big (}x\exp(-c(\ln x)^{3/5}(\ln \ln x)^{-1/5}){\Big )},

ce qui est encore bien loin de ce qu'on sait démontrer si l'hypothèse de Riemann est vraie

\pi (x)=\int _{2}^{x}{\frac {\mathrm {d} u}{\ln u}}+O({\sqrt {x}}\ln x).

Le nombre premier de rang n

En 1902, Cipolla montra le développement asymptotique

p_{n}=n\left\{\ln n+\ln \ln n-1+{\frac {\ln \ln n-2}{\ln n}}-{\frac {(\ln \ln n)^{2}-6\ln n+11}{(\ln n)^{2}}}+O\left(\left({\frac {\ln \ln n}{\ln n}}\right)^{3}\right)\right\}

Grâce à une étude numérique de la fonction $ζ$ , Rosser et Schoenfeld ont montré, pour n supérieur ou égal à 20, que

n\left(\ln n+\ln \ln n-{\frac {3}{2}}\right)<p_{n}<n\left(\ln n+\ln \ln n-{\frac {1}{2}}\right).

La borne inférieure a été améliorée par Dusart en 1999 qui montra, pour n >1,

n{\Big (}\ln n+\ln \ln n-1{\Big )}<p_{n}.

Notes et références

Notes

Les séries de Dirichlet sont une généralisation des séries de Riemann avec un numérateur différent de 1 et qui forme une suite indicée par n.
Il est aussi possible de calculer $ζ(2 k)$ à l'aide de l'égalité de Parseval. Voir à ce propos la page Exercices sur les séries de Fourier et la fonction zêta sur Wikiversité.
On trouvera par exemple quatorze démonstrations (en anglais) de la valeur $ζ(2) = π 2 /6$ sur le site internet de Robin Chapman.
Cette méthode de prolongement s'étend aux séries de Dirichlet générales.
Pour une généralisation de cette section aux fonctions zêta de Hurwitz, avec une preuve plus simple, voir cet exercice corrigé sur Wikiversité.
Le pôle en $1$ de $ζ$ est annulé par le terme 1 – 2^{1 – s} ; on a $\eta (1)=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}}{n}}=\ln 2$ (la série harmonique alternée).
Il existe d'autres démonstrations : on peut par exemple montrer que la série est en fait convergente pour $Re(s)$ > 0 en appliquant la formule de Cahen pour l'abscisse de convergence simple, les sommes partielles des coefficients ne prenant que l'une des trois valeurs 0, 1, 2. On peut aussi effectuer sur la série un regroupement des termes de la forme ${\frac {1}{(3n-2)^{s}}}+{\frac {1}{(3n-1)^{s}}}$ en laissant le terme négatif à part. Ce faisant, la série est alors une série alternée dont les termes sont décroissants (cela se montre facilement car on a 3n – 2 < 3n – 1 < 3n < 3n + 1 < 3n + 2 donc ${\frac {1}{3n-2}}+{\frac {1}{3n-1}}>{\frac {2}{3n}}$ d'une part et ${\frac {2}{3n}}>{\frac {1}{3n+1}}+{\frac {1}{3n+2}}$ d'autre part) et qui converge donc par application du critère des séries alternées pour s réel. On montre facilement que la série ne converge pas en 0 car ses sommes partielles ne tendent pas vers 0.
La présence du facteur 1 – 2^{1 – s} dans la formule de Ramaswami montre que le prolongement de $ζ$ par cette formule souffre du même problème que celui par la fonction $η$ de Dirichlet.
L'expression : $ζ$ (a) = $η$ (a)/(1 – 2^{1 – a}) pour a ∈ ]0, $+\infty$ [\{1} donne le même résultat puisque l'expression $η$ (a) de la fonction $η$ de Dirichlet est positive par le théorème des séries alternées et que 1 – 2^{1 – a} est du même signe que a – 1.
L'article détaillé hypothèse de Riemann précise bien qu'il ne s'agit pas d'une estimation approchée de cette partie réelle, mais d'une démonstration, sans aucune incertitude numérique.

Références

(en) Lennart Råde et Bertil Westergren, Mathematics Handbook for Science and Engineering, 2004, 562 p. (ISBN 978-3-540-21141-9, lire en ligne), p. 194.
Tanguy Rivoal, « La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs », Comptes rendus de l'Académie des sciences, i, vol. 331, n^o 4,‎ 2000, p. 267-270 (DOI 10.1016/S0764-4442(00)01624-4, Bibcode 2000CRASM.331..267R, arXiv math/0008051).
(en) Wadim Zudilin, « One of the numbers ζ(5), ζ(7), ζ(9), ζ(11) is irrational », Russ. Math. Surv. (en), vol. 56, n^o 4,‎ 2001, p. 774-776 (DOI 10.1070/RM2001v056n04ABEH000427, Bibcode 2001RuMaS..56..774Z).
Stéphane Fischler, « Irrationalité de valeurs de zêta », Séminaire Bourbaki, vol. 44, n^o 910,‎ novembre 2002 (lire en ligne).
(en) Tatiana R. Cardoso et Antonio S. de Castro, « The Blackbody Radiation in D-Dimensional Universes », sur arXiv, septembre 2005.
G. H. Hardy et E. M. Wright (trad. de l'anglais par F. Sauvageot), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »], Paris/Heidelberg, Vuibert-Springer, 2007, 568 p. (ISBN 978-2-7117-7168-4), p. 321-330.
Ellison et Mendès France, p. 75.
(de) H. von Mangoldt, « Beweis der Gleichung $\sum \limits _{k=1}^{\infty }{\frac {\mu (k)}{k}}=0$ », Berl. Ber.,‎ 1897, p. 835-852.
(de) E. Landau, « Über die Äquivalenz zweier Hauptsätze der analytische Zahlentheorie », Wien. Ber., vol. 120,‎ 1911, p. 973-988.
(en) Władysław Narkiewicz, The Development of Prime Number Theory : From Euclid to Hardy and Littlewood, Springer, 2000 (lire en ligne), p. 285-286.
Tenenbaum 2008, p. 248.
Ou la redémontrer directement par la même méthode qui, dans le cas particulier des fonctions zêta de Hurwitz (dont fait partie la fonction $ζ$ de Riemann), est élémentaire : voir cet exercice corrigé sur Wikiversité.
(en) Neal Koblitz, P-adic Numbers, p-adic Analysis, and Zeta-Functions, coll. « GTM » (n^o 58), 1984, 2^e éd. (1^re éd. 1977) (lire en ligne), p. 47.
Voir Tenenbaum 2008, p. 253 ; P. Cartier, « An Introduction to Zeta-Functions », in (en) M. Waldschmidt, P. Moussa, J.-M. Luck et C. Itzykson (éds.), From Number Theory to Physics [détail des éditions], p. 5-12, et surtout 11-12, suivi ici (aperçu sur Google Livres).
Lang 1970, p. 157.
(en) David Vernon Widder, The Laplace Transforms, PUP, 1946 (lire en ligne), p. 230.
Lang 1970, p. 158.
(en) V. Ramaswami, « Notes on Riemann's ζ-function », J. London Math. Soc., vol. 9, n^o 3,‎ 1934, p. 165-169 (DOI 10.1112/jlms/s1-9.3.165).
Ivić 1985, p. 4-5.
(en) Y. Matsuoka, « Generalized Euler Constants Associated with the Riemann Zeta Function », Number Theory and Combinatorics, World Scientific,‎ 1985, p. 279-295.
(en) Luis Baez-Duarte, « Fast proof of functional equation for ζ(s) »,‎ 2003 (arXiv math/0305191).
On peut aussi, comme le fait Tenenbaum 2008, p. 233-234 (p. 142 de l'édition en anglais), le déduire de la définition par une intégrale de contour.
Voir l'article 1 + 2 + 3 + 4 + ⋯.
(en) I. M. Vinogradov, Elements of Number Theory, Dover, 2003, 227 p. (ISBN 978-0-486-49530-9, lire en ligne), p. 38 ; (en) J. E. Nymann, « On the probability that k positive integers are relatively prime », J. Number Theory, vol. 4, n^o 5,‎ 1972, p. 469-473 (DOI 10.1016/0022-314X(72)90038-8) ; (en) Richard A. Mollin, Advanced Number Theory with Applications, CRC Press, coll. « Discrete Mathematics and Its Applications », 2009, 440 p. (ISBN 978-1-4200-8329-3, lire en ligne), p. 220.
(de) A. Walfisz, Weylsche Exponentialsummen in der neueren Zahlentheorie, Berlin, VEB Deutscher Verlag der Wissenschaften, 1963.
(de) F. Mertens, « Ueber eine Eigenschaft der Riemann'schen $ζ$ -Function », Wien. Ber., vol. 107,‎ 1898, p. 1429-1434.
Article de Laforgia et Natalini.
Article de Ahsan, Lam-Estrada, Lopez-Bonilla et Lopez-Vazquez.
(en) Kevin Ford, « Vinogradov's integral and bounds for the Riemann zeta Function », Proc. London Math. Soc., vol. 85,‎ 2002, p. 565-633.
Voir par exemple (en) E. C. Titchmarsh, The Theory of Functions, Oxford University Press, 1932, § 5.65.
(en) M.N. Huxley, « Exponential sums and the Riemann zeta function. V. », Proc. London Math. Soc. (3), vol. 90, n^o 1,‎ 2005, p. 1-41.
Titchmarsh et Heath-Brown 1987, chap. IX, « General distribution of zeros ».
(en) Vinogradov, « A new estimate for $|ζ(1 + i t)|$ », Izv. Akad. Nauk SSSR Ser Math., vol. 22,‎ 1958, p. 161-164 ; Titchmarsh et Heath-Brown 1987, p. 135.
(en) C. Yalçın Yıldırım, « A note on $ζ''$ (s) and $ζ'''$ (s) », Proc. Amer. Math. Soc., vol. 124, n^o 8,‎ août 1996 (lire en ligne).
(en) H. L. Montgomery, « The pair correlation of zeros of the zeta function », dans Analytic number theory (Proceedings of Symposium in Pure Mathemathics, vol. 24, St. Louis Univ., St. Louis, Mo., 1972), AMS, Providence, R.I., 1973, p. 181-193.
(en) Michael V. Berry, « Riemann's zeta function: a model for quantum chaos? », dans T. H. Seligman et H. Nishioka, Quantum Chaos and Statistical Nuclear Physics, Springer-Verlag, coll. « Springer Lecture Notes in Physics » (n^o 263), 1986 (lire en ligne), p. 1-17.
(en) Michael V. Berry, « Semiclassical formula for the number variance of the Riemann zeros », Nonlinearity, vol. 1,‎ 1988, p. 399-407 (lire en ligne).
(en) Michael V. Berry, « Quantum mechanics, chaos and the Riemann zeros », dans A. O. Barut, I. D. Feranchuk, Ya. M. Shnir et L. M. Tomil'chik, Quantum Systems: New Trends and Methods, World Scientific, 1995 (lire en ligne), p. 387-392.
(en) Michael V. Berry et Jonathan P. Keating, « H = xp and the Riemann zeros », dans I. V. Lerner et J. P. Keating, Supersymmetry and Trace Formulae: Chaos and Disorder, New York, Plenum Press, 1999 (lire en ligne), p. 355-367.
(en) Michael V. Berry et Jonathan P. Keating, « The Riemann Zeros and Eigenvalue Asymptotics », SIAM Review, vol. 41,‎ 1999, p. 236-266 (lire en ligne).
Propriétés statistiques de la fonction zêta :
- (en) Eugene B. Bogomolny et Jonathan P. Keating, « Random matrix theory and the Riemann zeros I : three- and four-point correlations », Nonlinearity, vol. 8,‎ 1995, p. 1115-1131 ;
- (en) Eugene B. Bogomolny et Jonathan P. Keating, « Random matrix theory and the Riemann zeros II : n-point correlations », Nonlinearity, vol. 9,‎ 1996, p. 911-935 ;
- (en) Oriol Bohigas, Patricio Lebœuf et M.-J. Sanchez, « Spectral spacing correlations for chaotic and disordered systems », Foundations of Physics, vol. 31,‎ 2001, p. 489-517 (arXiv nlin.CD/0012049) ;
- (en) Francesco Mezzadri, « Random matrix theory and the zeros of zeta'(s) », Journal of Physics A: Mathematical and General, vol. 36,‎ 2003, p. 2945-2962 (arXiv math-ph/0207044) ;
- (en) Jonathan P. Keating, « Random matrices and the Riemann zeta-function – a review », dans James M. Hill et Ross Moore, Applied Mathematics Entering the 21st Century : Invited Talks from the ICIAM 2003 Congress, SIAM, 2004, p. 210-225 ;
- (en) Eugene Bogomolny, Oriol Bohigas, Patricio Lebœuf et A. G. Monastra, « On the spacing distribution of the Riemann zeros: corrections to the asymptotic result », Journal of Physics A: Mathematical and General, vol. 39,‎ 2006, p. 10743-10754 (arXiv math/0602270).
On pourra lire également : Philippe Biane, « La fonction zêta de Riemann et les probabilités », 2003, Journées X-UPS.
E043, Commentarii Academiæ Scientiarum imperialis petropolitanæ, t. VII, 1734-1735, p. 156-157.
Exercices de calcul intégral sur divers ordres de transcendantes et sur les quadratures, t. II, 1811, p. 65.

Voir aussi

Livres en français

André Blanchard, Initiation à la théorie analytique des nombres premiers, Paris, Dunod, 1969
Jean-Benoît Bost, Pierre Colmez et Philippe Biane, La Fonction Zêta, Paris, Éditions de l'École polytechnique, 2002, 193 p. (ISBN 2-7302-1011-3)
Suite d'articles sur différents points de la théorie analytique des nombres et de la fonction zêta. N'est pas destiné à une étude systématique de la fonction zêta de Riemann, en ligne Bost, Colmez et Biane sous forme pdf.
Pierre Colmez, Éléments d'analyse et d'algèbre (et de théorie des nombres), Éditions de l'École Polytechnique, 2009 (lire en ligne)
On y trouvera en particulier une démonstration du théorème des nombres premiers et de celui de la progression arithmétique.
William John Ellison et Michel Mendès France, Les Nombres premiers, 1975 [détail de l’édition]
Malgré son titre, il s'agit essentiellement de l'étude de la fonction zêta de Riemann. On y trouvera aussi une preuve élémentaire du théorème de Hadamard-La Vallée Poussin, une preuve du théorème de Dirichlet et la démonstration de la région sans zéro de Vinogradov-Korobov. À lire pour commencer. Il a aussi l'avantage d'être en français.
Jean Favard, Leçons sur les fonctions presque-périodiques, Paris, Gauthier-Villars, 1933
Pour comprendre la théorie de Bohr des séries de Dirichlet dont la fonction zêta fait partie puisqu'elle est presque périodique au sens de Bohr dans le demi-plan à droite du pôle 1.
Gérald Tenenbaum, Introduction à la théorie analytique et probabiliste des nombres, Paris, Belin, 2008, 3^e éd., 590 p. (ISBN 978-2-7011-4750-5)

Livres en anglais

Eberhard Freitag et Rolf Busam, Complex Analysis, Springer, 2^e édition, 2009 (ISBN 978-3-540-25724-0) — La théorie analytique des nombres, de la définition des nombres complexes aux formes modulaires en passant par zêta.
Aleksandar Ivić, The Riemann Zeta-Function, John Wiley & Sons, 1985 (ISBN 0-471-80634-X, lire en ligne) — Concurrent du traité de Titchmarsh, un peu plus récent.
Karatsuba, Basic Analytic Number Theory, Springer-Verlag, 1993 (ISBN 0-387-53345-1) — Très bon traité.
Serge Lang, Algebraic Number Theory, Addison Wesley, 1970
(en) E. C. Titchmarsh et D. R. Heath-Brown, The Theory of the Riemann Zeta-Function, Oxford, OUP, 1987, 2^e éd., 412 p. (ISBN 0-19-853369-1) — La bible sur la fonction zêta jusqu'à une époque récente, disons 1990. Reste irremplaçable sur certains sujets. La première édition de 1951 n'a pas beaucoup été complétée par la seconde de 1986. Heath-Brown s'est contenté d'indiquer pour chaque chapitre l'état des connaissances en 1986 sans démonstration en deux ou trois pages.
S. J. Patterson (de), An Introduction to the Theory of the Riemann Zeta-Function, coll. « Cambridge Studies in Advanced Mathematics » (n^o 14), Cambridge University Press, 1995 (ISBN 0-521-49905-4)

Articles de revue

Michel Balazard, « Un siècle et demi de recherches sur l'hypothèse de Riemann », Gazette des mathématiciens, vol. 126,‎ 2010, p. 7-24 (lire en ligne)
(en) Nicholas M. Katz et Peter Sarnak, « Zeroes of zeta functions and symmetry », Bull. Amer. Math. Soc., vol. 36,‎ 1999, p. 1-26 (lire en ligne)
(en) Philippe Biane, Jim Pitman et Marc Yor, « Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions », Bull. Amer. Math. Soc., vol. 38,‎ 2001, p. 435-465 (lire en ligne)
(en) Stephen S. Gelbart et Stephen D. Miller, « Riemann's zeta function and beyond », Bull. Amer. Math. Soc., vol. 41, n^o 1,‎ 2004, p. 59-112 (lire en ligne)

Liens externes

Page personnelle de Tanguy Rivoal, et en particulier cet article sur les zéros de la fonction ζ
Historique d'articles en français et en anglais sur la fonction $ζ$ de Riemann
(en) Eric W. Weisstein, « Riemann Zeta Function », sur MathWorld

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

Fonction zêta de Riemann

Premiers travaux sur la fonction zêta par Euler et Riemann

Prologue

Premières considérations sur la fonction

Définition par la série de Riemann

Valeurs de la fonction zêta pour s entier pair non nul

Valeurs de la fonction zêta pour s entier impair

Valeurs numériques particulières utilisées en physique

Développements en série de Dirichlet en lien avec quelques fonctions arithmétiques

Produit eulérien

Lien avec la répartition des nombres premiers

Expression intégrale

Dérivées de la fonction zêta

Que devient la série de Riemann sur l'axe Re(s) = 1 ?

Extension à ℂ \ {1}

Par la formule d'Euler-Maclaurin

Par une intégrale sur ℝ+

Par une intégrale de contour

Par la formule sommatoire d'Abel

Par la fonction êta de Dirichlet

Par la formule de Landau ou celle de Ramaswami

Propriétés diverses de la fonction

Comportement asymptotique

Développement de Laurent au voisinage de 1

Relation fonctionnelle

Valeurs de la fonction zêta pour s entier négatif ou nul

Définition de ln ζ et de sa dérivée

Présentation élémentaire pour les nombres complexes du demi-plan Re(s) > 1

Convergence des séries de Dirichlet de ln ζ, 1 / ζ et ζ' / ζ sur la droite Re(s) = 1

Extension de ln ζ à Re(s) ≤ 1

Représentation de 1/ζ et fonction M de Mertens

Inégalités

Inégalité de Mertens

Inégalité de Laforgia et Natalini

Inégalité de Ahsan, Lam-Estrada, Lopez-Bonilla et Lopez-Vazquez

Estimation de la fonction dans les diverses régions du plan

Presque périodicité

Estimations dans la région Re(s) > 1

Estimations sur Re(s) = 1

Estimations sur Re(s) = 0

Estimations dans la région Re(s) < 0

Estimation dans la bande critique

Le théorème de Valiron

La relation fonctionnelle approchée

La théorie de la fonction mu

Les zéros

Les zéros triviaux

Les zéros non triviaux

Représentation sous forme de produit de facteurs primaires (produit de Hadamard)

Expressions de ζ'/ζ en fonction des zéros triviaux et non triviaux

La bande critique et l'hypothèse de Riemann

La fonction S(T)

La région sans zéro

Les grandes conjectures

L'hypothèse de Riemann

Conséquences de l'hypothèse de Riemann sur la croissance de la fonction zêta

L'hypothèse de Riemann et les zéros de la dérivée ζ'

L'hypothèse de Lindelöf et l'hypothèse de densité

Les hypothèses de Mertens

La conjecture des paires corrélées

La conjecture de Hilbert-Polya

Propriétés statistiques des zéros non triviaux et chaos quantique

Le problème des moments

Applications diverses

Régularisation Zêta

Développement en série entière de ln Γ(1+t)

Suites de Farey et hypothèse de Riemann

Fonction de comptage des nombres premiers et théorème des nombres premiers

Le nombre premier de rang n

Notes et références

Notes

Références

Voir aussi

Livres en français

Livres en anglais

Articles de revue

Articles connexes

Liens externes

Que devient la série de Riemann sur l'axe $Re(s)$ = 1 ?

Par une intégrale sur ℝ⁺

Définition de $ln ζ$ et de sa dérivée

Convergence des séries de Dirichlet de $ln ζ$ , $1 / ζ$ et $ζ' / ζ$ sur la droite Re(s) = 1

Extension de $ln ζ$ à Re(s) ≤ 1

Estimations dans la région $Re(s)$ > 1

Estimations sur $Re(s)$ = 1

Estimations sur $Re(s)$ = 0

Estimations dans la région $Re(s)$ < 0

L'hypothèse de Riemann et les zéros de la dérivée $ζ'$