Fonction nombre de diviseurs
En théorie des nombres — une branche des mathématiques — la fonction nombre de diviseurs est une fonction arithmétique qui indique le nombre de diviseurs d'un entier naturel non nul n, en incluant parmi les diviseurs de n les nombres 1 et n. Elle est généralement notée d ou τ (de l'allemand Teiler : diviseur), ou encore σ0, comme cas particulier de fonction somme des puissances k-ièmes des diviseurs.
Définition
Pour tout nombre naturel n on définit :
- .
Les premières valeurs sont les suivantes[1] :
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diviseurs de n | 1 | 1, 2 | 1, 3 | 1, 2, 4 | 1, 5 | 1, 2, 3, 6 | 1, 7 | 1, 2, 4, 8 | 1, 3, 9 | 1, 2, 5, 10 | 1, 11 | 1, 2, 3, 4, 6, 12 |
| d(n) | 1 | 2 | 2 | 3 | 2 | 4 | 2 | 4 | 3 | 4 | 2 | 6 |
Propriétés
- On a l'identité suivante : où désigne la fonction partie entière [2] - [3] - [4] :
- Si la décomposition en produit de facteurs premiers de n est
- ,
- alors[5] :
- .
- La fonction nombre de diviseurs est donc multiplicative, c.-à-d. que si m et n sont premiers entre eux, alors :
- .
- Un nombre n est premier si et seulement si d(n)=2.
- Un nombre n est un carré parfait si et seulement si d(n) est impair.
- est le double du nombre de diviseurs de n entre 1 et √n, auquel il faut retrancher 1 si n est un carré parfait, donc un majorant de d(n) est 2√n.
- La fonction génératrice de (d(n)) s'exprime comme série de Lambert :
- (pour )
- La série de Dirichlet de (d(n)) est le carré de la fonction zêta de Riemann[6] :
- (pour )
Comportement asymptotique
Formule de Dirichlet
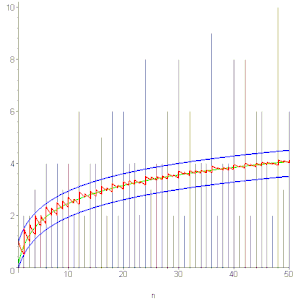
La fonction d est très irrégulière : elle prend la valeur 2 pour n premier, et prend aussi des valeurs arbitrairement grandes (par exemple N + 1 pour n = 2N) . Mais en moyenne de Cesàro : .
Ceci vient de la formule , dont on déduit : où (Hn) est la série harmonique, puis l'encadrement :
.
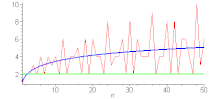
Un développement plus précis est donné par [2] - [7] - [8] - [4]
(où O est un symbole de Landau et γ la constante d'Euler-Mascheroni.)
Il a été démontré par Johann Peter Gustav Lejeune Dirichlet en 1849 [9].
On en déduit qu'un ordre moyen pour d(n) est ln n + 2γ.
Problème des diviseurs de Dirichlet
La recherche des valeurs de telles que
constitue le « problème des diviseurs de Dirichlet (en) »[3].
Des avancées ont été effectuées par Gueorgui Voronoï (1903, O(√x) remplacé par O(3√x log(x))[10], Johannes van der Corput (1922, β = 33100)[11], ainsi que Martin Huxley (de) (2003, β = 131416)[12]. À l'opposé, Godfrey Harold Hardy et Edmund Landau ont démontré[13] que β est nécessairement supérieur ou égal à 1/4. Les valeurs possibles pour β font toujours l'objet de recherches.
Application à la différence du nombre de diviseurs pairs et du nombre de diviseurs impairs
Posons où est le nombre de diviseurs pairs de n et celui des diviseurs impairs ; la suite est répertoriée comme suite A048272 de l'OEIS.
On a alors l'identité : qui, combinée avec la valeur de la série harmonique alternée ,
donne la converge au sens de Cesàro de vers .
La formule de Dirichlet permet d'obtenir plus précisément : .
Plus petit entier ayant un nombre prescrit de diviseurs
Notons le plus petit n tel que ; la suite est répertoriée comme suite A005179 de l'OEIS.
Le tableau suivant en donne les 36 premiers termes.
| Nombre de diviseurs | Factorisation de | |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 4 | 22 |
| 4 | 6 | 2·3 |
| 5 | 16 | 24 |
| 6 | 12 | 22·3 |
| 7 | 64 | 26 |
| 8 | 24 | 23·3 |
| 9 | 36 | 22·32 |
| 10 | 48 | 24·3 |
| 11 | 1 024 | 210 |
| 12 | 60 | 22·3·5 |
| 13 | 4 096 | 212 |
| 14 | 192 | 26·3 |
| 15 | 144 | 24·32 |
| 16 | 120 | 23·3·5 |
| 17 | 65 536 | 216 |
| 18 | 180 | 22·32·5 |
| 19 | 262 144 | 218 |
| 20 | 240 | 24·3·5 |
| 21 | 576 | 26·32 |
| 22 | 3 072 | 210·3 |
| 23 | 4 194 304 | 222 |
| 24 | 360 | 23·32·5 |
| 25 | 1 296 | 24·34 |
| 26 | 12 288 | 212·3 |
| 27 | 900 | 22·32·52 |
| 28 | 960 | 26·3·5 |
| 29 | 268 435 456 | 228 |
| 30 | 720 | 24·32·5 |
| 31 | 1 073 741 824 | 230 |
| 32 | 840 | 23·3·5·7 |
| 33 | 9 216 | 210·32 |
| 34 | 196 608 | 216·3 |
| 35 | 5 184 | 26·34 |
| 36 | 1 260 | 22·32·5·7 |
Nota 1 : Pour p,q premiers tels que , et .
Nota 2 : si n'a pas de successeur plus petit que lui, alors il est hautement composé.
Généralisation
La fonction associe à tout naturel non nul la somme des puissances -ièmes de ses diviseurs :
La fonction nombre de diviseurs est donc le cas particulier de cette fonction obtenu pour :
- .
Notes et références
- Pour plus de valeurs, voir la suite A000005 de l'OEIS.
- Pierre Eymard et Jean-Pierre Lafon, Autour du nombre Pi, Hermann, p. 25-29
- Olivier Bordellès, « Le problème des diviseurs de Dirichlet », Quadrature, no 71, , p. 21-30 (lire en ligne).
- Gérald Tenenbaum, Introduction à la théorie analytique et probabiliste des nombres, Dunod, chap. 1.3 (« Sur les ordres moyens, en illustration du principe de l'hyperbole de Dirichlet »)
- (en) G. H. Hardy et E. M. Wright, An Introduction to the Theory of Numbers (1re éd. 1938) [détail des éditions], 4e éd., 1975, p. 239, Th. 273.
- Hardy Wright, p. 250, Th. 289.
- Hardy Wright, p. 264, Th. 320.
- G.H. Hardy et E.M. Wright (trad. François Sauvageot), Introduction à la théorie des nombres, Vuibert Springer, , chap. XVIII, section 18.2, théorème 320, p. 339
- (de) P. G. L. Dirichlet, « Über die Bestimmung der mittleren Werthe in der Zahlentheorie », Abhandl. König. Preuss. Akad. Wiss., , p. 69-83 ou (de) P. G. L. Dirichlet, Werke, t. II, 49-66 p..
- G. Voronoï, « Sur un problème du calcul des fonctions asymptotiques », J. reine angew. Math., vol. 126, , p. 241-282 (lire en ligne).
- (de) J. G. van der Corput, « Verschärfung der Abschätzung beim Teilerproblem », Mathematische Annalen, vol. 87, , p. 39-65. « —, Corrections », vol. 89, 1923, p. 160.
- (en) M. N. Huxley, « Exponential Sums and Lattice Points III », Proc. London Math. Soc., vol. 87, no 3, , p. 591-609.
- (en) G. H. Hardy, « On Dirichlet’s divisor problem », Proc. Lond. Math. Soc. (2), vol. 15, , p. 1-25. Cf. Hardy Wright, p. 272.
- Les deux premières colonnes sont extraites de la suite A005179 de l'OEIS. Pour premiers tels que , et .
Articles connexes
- Nombre parfait
- Nombre hautement composé
- Suite aliquote, suite où chaque nombre est la somme des diviseurs propres de son prédécesseur.
- Constante d'Erdős-Borwein égale à .




















































