Fonction convexe
En mathématiques, une fonction réelle d'une variable réelle est dite convexe :
- si quels que soient deux points et du graphe de la fonction, le segment est entièrement situé au-dessus du graphe, c’est-à-dire que la courbe représentative de la fonction se situe toujours en dessous de ses cordes ;
- ou si l'épigraphe de la fonction (l'ensemble des points qui sont au-dessus de son graphe) est un ensemble convexe ;
- ou si vu d'en dessous, le graphe de la fonction est en bosse.
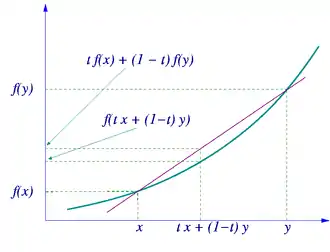
En précisant au moyen des valeurs de la fonction ce que sont les points et ci-dessus, on obtient une définition équivalente souvent donnée de la convexité d'une fonction : une fonction définie sur un intervalle réel est convexe lorsque, pour tous et de et tout dans on a :
Lorsque l'inégalité est stricte (avec différent de et dans ), on parle de fonction strictement convexe.
La fonction carré et la fonction exponentielle sont des exemples de fonctions strictement convexes sur l'ensemble réel .
Ces définitions se généralisent aux fonctions définies sur un espace vectoriel (ou affine) arbitraire et à valeurs dans la droite réelle achevée .
À l'inverse, une fonction dont un même segment est situé en dessous du graphe, ou dont l'hypographe (l'ensemble des points qui sont en dessous du graphe de la fonction) est un ensemble convexe, ou encore dont, vu d'en dessous, le graphe est en creux, est dite concave. En d'autres termes, une fonction est concave si son opposée est convexe. Ainsi, les fonctions affines sont à la fois convexes et concaves.
Les fonctions convexes sont, avec les ensembles convexes, les objets constitutifs de l'analyse convexe, une discipline « intermédiaire » entre l'algèbre linéaire et l'analyse non linéaire. Elles permettent de démontrer un grand nombre d'inégalités remarquables, dites inégalités de convexité. Elles jouent aussi un rôle singulier en optimisation, en supprimant la distinction entre minima locaux et globaux (tout minimum local d'une fonction convexe est un minimum global).
Fonction convexe d'une variable réelle
Dans cette première section, on va supposer que l'ensemble de départ est un intervalle réel . Cette restriction permet de fournir une première initiation aux fonctions convexes d'abord plus aisée et parce que la possibilité de tracer des représentations graphiques planes facilite certainement la tâche, ensuite et surtout parce que les concepts de continuité ou dérivabilité sont significativement plus maniables pour les fonctions d'une seule variable. Cette approche montre tout de même vite ses limites, en particulier parce qu'elle n'est guère pertinente pour appliquer la théorie des fonctions convexes à l'optimisation qui en est sans doute la principale motivation.
Définitions
Définition — Une fonction d'un intervalle réel vers est dite convexe lorsque, pour tous et de et tout dans on a :
Cela signifie que pour tout et de , le segment de , où et , est situé au-dessus de la courbe représentative de .
Une fonction concave est une fonction dont la fonction opposée est convexe.
On vérifie aussitôt ce qui suit, reliant les notions d'ensemble convexe et de fonction convexe :
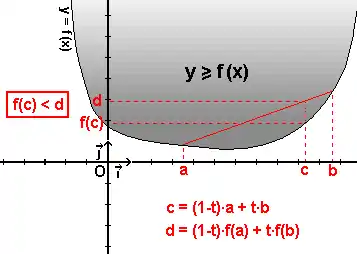
Remarque — La fonction est convexe sur si et seulement si son épigraphe est un sous-ensemble convexe de .
- Exemple
- La fonction est convexe, parce que son épigraphe est un quart de plan (lui-même convexe comme intersection de deux demi-plans). Il est souvent malcommode de vérifier la convexité d'une fonction définie par une formule concrète à partir de la seule définition, on attendra donc quelques paragraphes pour donner d'autres exemples, lorsqu'on disposera d'un critère de convexité plus utilisable en pratique.
Possibilité de n'utiliser que des milieux
La définition de la convexité fait apparaître des barycentres où les coefficients sont des réels arbitraires de . Lorsqu'on ne fait porter l'hypothèse que sur les milieux, elle s'étend aux isobarycentres :
Lemme[1] — Si une fonction vérifie la condition suivante pour , alors elle la vérifie pour tout entier :
En ajoutant une hypothèse supplémentaire de régularité[3] de , on obtient :
Extension à des barycentres de plus de deux points
L'inégalité de la définition s'étend comme suit (on peut le démontrer par récurrence sur l'entier [6] ou par le même argument que dans la proposition ci-dessus[7]. On dénomme parfois cette version l'inégalité de Jensen :
Proposition — Si est convexe sur et si sont des points de et des réels positifs ou nuls tels que , alors :
Géométrie du graphe d'une fonction convexe
On appelle parfois « lemme des trois cordes » ou « inégalité des pentes » voire « inégalité des trois pentes » le résultat suivant[8] :
Proposition[9] — Si est convexe sur pour tous points , et de avec :
Réciproquement, si l'une des deux inégalités est vérifiée pour tous , et de avec , alors est convexe.
Régularité des fonctions convexes
Le « lemme des trois cordes » permet de montrer que[10] :
Théorème — Si est un intervalle ouvert et si est convexe alors :
- est dérivable à gauche et à droite (donc continue) et ;
- les fonctions , sont croissantes ;
- l'ensemble des points où n'est pas dérivable (c'est-à-dire tels que ) est au plus dénombrable.
On peut préciser les deux premiers points par[11] : une fonction définie sur un intervalle ouvert est convexe si et seulement si et sont définies et croissantes sur .
On démontre par ailleurs (voir infra) que est aussi localement lipschitzienne.
Cas des fonctions dérivables
On dispose de deux caractérisations[12] :
Proposition — Soit une fonction dérivable sur un intervalle .
- est convexe si et seulement si sa courbe représentative est au-dessus de chacune de ses tangentes ;
- est convexe si et seulement si sa dérivée est croissante sur .
On déduit de la seconde caractérisation :
- que toute fonction convexe et dérivable (sur un intervalle réel) est de classe C1[13] ;
- le corollaire suivant, fort pratique pour vérifier sans mal la convexité d'exemples spécifiques :
Corollaire[14] — Soit une fonction deux fois dérivable sur un intervalle .
est convexe si et seulement si sa dérivée seconde est à valeurs positives ou nulles.
Ainsi, on peut désormais facilement ajouter à sa collection de fonctions convexes (ou concaves) les exemples suivants :
- la fonction puissance est concave si et convexe sinon ;
- pour tout entier positif , la fonction est convexe si est pair (si est impair, elle est convexe sur et concave sur ) ;
- la fonction est convexe ;
- la fonction est concave.
Stricte convexité
En faisant intervenir des inégalités strictes, on dispose d'une variante de la convexité : la stricte convexité.
Définition — Une fonction d'un intervalle de vers est dite strictement convexe lorsque, pour tous et distincts dans et tout dans , on a :
Les résultats énoncés plus haut pour des fonctions convexes s'adaptent généralement sans mal aux fonctions strictement convexes.
De même que les fonctions dérivables convexes sont celles qui ont une dérivée croissante, les fonctions dérivables strictement convexes sont celles qui ont une dérivée strictement croissante.
D'après le lien entre monotonie et signe de la dérivée, une fonction deux fois dérivable est donc strictement convexe si et seulement si est positive et ne s'annule que sur un ensemble d'intérieur vide.
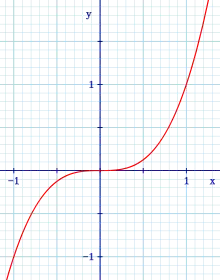
- Exemple
- est strictement convexe (sa dérivée seconde est positive et ne s'annule qu'en 0.
Fonction convexe définie sur un espace vectoriel
Convexité
On peut donner au moins deux définitions légèrement différentes d'une fonction convexe de plusieurs variables réelles (ou plus généralement : d'une variable vectorielle), qui reviennent essentiellement au même mais ne fournissent néanmoins pas exactement les mêmes fonctions. On prendra donc garde au contexte lors d'une invocation d'une de ces définitions pour comprendre s'il s'agit ou non de fonctions susceptibles de prendre des valeurs infinies.
Définition 1 — Soient un espace vectoriel (ou affine) réel et un convexe de . On dit qu'une fonction
est convexe lorsque
Autrement dit : est convexe si sa « restriction » à tout segment est une fonction convexe de la variable réelle (voir supra)[15].
Étant donné une fonction convexe au sens de la définition 1, on peut lui associer une fonction convexe au sens de la définition 2 en la prolongeant hors de par la valeur ; réciproquement, étant donné une fonction convexe au sens de la définition 2, l'ensemble est un convexe et la restriction de à est une fonction convexe au sens de la définition 1. Les deux transformations sont réciproques l'une de l'autre : les deux définitions, quoique techniquement distinctes, décrivent bien la même notion.
Certaines sources requièrent de plus que soit non vide (dans la définition 1) ou que ne soit pas la constante (dans la définition 2) pour prévenir certaines exceptions désagréables dans quelques énoncés. Une telle fonction de dans est dite propre[16].
La définition 2 est plus récente que la définition 1 et fut introduite indépendamment par Rockafellar et Moreau[17]. Elle permet de définir une fonction convexe comme un seul « objet » (une fonction définie sur un espace vectoriel ayant une propriété bien particulière) et non comme un couple formé d'un ensemble convexe d'un espace vectoriel et d'une fonction à valeurs réelles définie sur cet ensemble convexe. La définition 2 est la plus communément utilisée en analyse convexe, pour les raisons suivantes : d'une part, elle allège souvent l'expression des résultats et, d'autre part, elle permet de ne pas devoir préciser le convexe sur lequel est définie une fonction convexe obtenue par l'une des constructions standards de l'analyse convexe, comme l'enveloppe supérieure, la fonction d'appui, la fonction marginale, la fonction conjuguée, la fonction duale en optimisation, etc.
Stricte convexité
Soit un espace vectoriel (ou affine) réel. On dit qu'une fonction est strictement convexe si, pour tous et distincts dans et tout dans , on a :
Forte convexité
Soit un espace normé. On dit qu'une fonction est fortement convexe, de module si, pour tous et dans et tout dans , on a :
On retrouve la notion de fonction convexe lorsque .
Exemples de fonctions convexes
Voici quelques exemples de constructions de fonctions convexes :
- produit d'une fonction convexe par un réel positif ;
- somme de deux fonctions convexes (de plus, si est strictement convexe et est convexe alors est strictement convexe) ;
- exponentielle d'une fonction convexe ou plus généralement, fonction composée d'une fonction réelle convexe croissante par une fonction convexe [18] ;
- fonction convexe polyédrique ;
- fonction d'appui d'un ensemble et plus généralement :
- fonction sous-linéaire,
- fonction conjuguée d'une fonction de dans ;
- fonction indicatrice d'un ensemble convexe ;
- fonction marginale dont les valeurs sont obtenues en minimisant une seconde fonction paramétrée par ses arguments.
Voici des exemples concrets de fonctions convexes ou concaves :
- les applications à la fois convexes et concaves sont les applications affines ;
- une forme quadratique , associée à une forme bilinéaire symétrique , est convexe si, et seulement si est positive. Elle est strictement convexe si et seulement si est définie positive ;
- la fonction log-det : sur le convexe des matrices définies positives (dans l'espace des matrices symétriques réelles d'ordre ) est concave.
Propriétés élémentaires
Pour tout espace vectoriel topologique de dimension infinie, il existe des fonctions convexes de domaine qui ne sont pas continues : par exemple les formes linéaires non continues sur .
Cependant, une proportion significative de résultats valables pour des fonctions convexes d'une variable se reproduisent à l'identique pour des fonctions convexes sur une partie d'un espace vectoriel, soit qu'on se ramène pour les prouver à considérer la restriction de la fonction à une droite, soit que la démonstration soit une simple révision de la version à une variable. En voici quelques-unes :
- une fonction convexe est une fonction dont l'épigraphe est convexe[19] ;
- dans un espace vectoriel topologique, une fonction qui vérifie l'inégalité de convexité pour les seuls milieux et qui est continue est convexe ;
- une fonction convexe vérifie l'inégalité de Jensen.
Minorante affine
La technique de minoration des fonctions convexes par des fonctions affines est une variante adaptée à l'analyse de l'utilisation des hyperplans d'appui en géométrie convexe. La forme analytique du théorème de Hahn-Banach permettrait de minorer directement une fonction convexe définie (et à valeurs finies) sur la totalité de son espace de départ. En revanche, dès que la fonction n'est pas définie partout, il faut poser quelques restrictions techniques[20].
Proposition — Soit un espace vectoriel topologique, une fonction convexe et continue définie sur un ouvert convexe non vide de et un point de .
Il existe alors une fonction affine continue qui minore et qui coïncide avec elle en .
On verra un peu plus bas que l'hypothèse de continuité est superflue en dimension finie (c'est une conséquence de la convexité). En revanche, la condition topologique sur est indispensable, même en une seule variable : pour la fonction convexe sur (dont le graphe est un demi-cercle) et , on ne peut trouver de fonction affine minorante au sens de la proposition précédente.
Utilisation des dérivées premières
Voici un premier résultat permettant de reconnaître la convexité d'une fonction au moyen de ses dérivées premières. On note la forme linéaire continue qu'est la différentielle de au point . Le point 2 ci-dessous signifie que l'approximation affine de en tout point est une minorante de ; le point 3 exprime la monotonie de la dérivée.
Convexité et dérivées premières — Soient un espace normé, un ouvert convexe de et une fonction différentiable. Alors, les propriétés suivantes sont équivalentes :
- est convexe sur ;
- ;
- .
Un résultat analogue permet de caractériser la stricte convexité d'une fonction. Il suffit de remplacer les inégalités ci-dessus par des inégalités strictes et de supposer que les points d'évaluation et diffèrent.
Stricte convexité et dérivées premières I — Soient un espace normé, un ouvert convexe de et une fonction différentiable. Alors, les propriétés suivantes sont équivalentes :
- est strictement convexe sur ;
- ;
- .
En dimension finie, les inégalités ci-dessus peuvent être renforcées[21].
Stricte convexité et dérivées premières II — Soient un espace vectoriel de dimension finie, une fonction de classe C1 et . Alors les propriétés suivantes sont équivalentes :
- est strictement convexe ;
- pour tout , il existe une fonction continue, strictement croissante, vérifiant et
- pour tout , il existe une fonction continue, strictement croissante, vérifiant et
.
On peut enfin caractériser la forte convexité au moyen des dérivées premières.
Forte convexité et dérivées premières — Soient un espace euclidien, un ouvert convexe de et une fonction différentiable. Alors, les propriétés suivantes sont équivalentes :
- est fortement convexe sur ;
- ;
- .
Utilisation des dérivées secondes
On note la forme bilinéaire continue et symétrique qu'est la différentielle seconde de au point .
Convexité et dérivées secondes — Soient un ouvert d'un espace normé et une fonction deux fois différentiable.
- est convexe si et seulement si pour tout point , la forme bilinéaire est positive.
- Si, pour tout point est définie positive, alors est strictement convexe.
Rappelons que la réciproque du second point est fausse (voir supra).
Fonctions convexes en dimension finie
Continuité sur un ouvert
Comme en dimension 1, une fonction convexe définie sur un ouvert de est forcément continue en tout point de l'ouvert. La démonstration va nous donner une information plus précise[22] :
Théorème — Une fonction convexe définie (et à valeurs finies) sur un ouvert de est localement lipschitzienne, donc continue et dérivable presque partout.
En dimension > 1, l'ensemble négligeable des points où n'est pas dérivable peut avoir la puissance du continu : considérer par exemple[23] l'application convexe .
Discontinuités au bord
À une variable, sur un intervalle non ouvert, on a vu qu'une fonction convexe n'était pas nécessairement continue.
Néanmoins il est possible de la rendre continue par un procédé simple : si est convexe sur un intervalle , alors nécessairement la limite à droite de en existe et est inférieure ou égale à la valeur . La discontinuité de en la borne se produit alors dans le cas où . On peut s'en démêler en modifiant simplement la valeur de en ce point : il suffit de la diminuer et la remplacer par [24].
Dès la dimension 2, les choses ne sont pas aussi confortables, comme le montre l'exemple suivant :
Soit le disque-unité fermé de ; considérons la fonction définie sur par :
Cette fonction est convexe. Elle est toutefois discontinue au point mais ici la discontinuité ne peut être levée par une simple modification de la valeur . On constate en effet que si on tend radialement vers ce point, la fonction étant nulle sur le rayon, tend vers 0 ; mais un calcul facile permet de constater que, si on tend vers le long du cercle frontière de , tend vers 2. Toutes les valeurs comprises entre 0 et 2 sont d'ailleurs valeurs d'adhérence de au point et il est définitivement illusoire d'espérer rendre cette continue en modifiant ses valeurs sur le bord[25].
Toutefois, si l'ensemble de définition est un polytope, les choses se passent comme sur les intervalles de , comme on peut le voir en appliquant le théorème suivant[26] :
Théorème — Une fonction convexe bornée définie sur l'intérieur d'un polytope admet un prolongement convexe continu au polytope.
Fermeture d'une fonction convexe
Une fois qu'on a compris qu'il est vain de vouloir modifier une fonction convexe sur la frontière de son domaine de définition jusqu'à la rendre continue, on peut néanmoins choisir un jeu de valeurs sur cette frontière plus remarquable que les autres, en exigeant que le prolongement soit à la fois semi-continu inférieurement (ce qui nécessite de choisir des valeurs faibles) et convexe (ce qui nécessite de les prendre fortes).
Pour écrire l'énoncé assez confortablement, il est ici particulièrement approprié d'utiliser des fonctions définies sur tout et prenant éventuellement la valeur .
Théorème — Soit une fonction convexe de domaine effectif . On note la fonction définie en par :
La fonction est alors caractérisée par l'une au choix des trois propriétés suivantes :
- coïncide avec en les points qui ne sont pas sur la frontière relative du convexe ; elle est convexe et semi-continue inférieurement ;
- coïncide avec en les points qui ne sont pas sur la frontière relative de et, pour tout point de la frontière relative de et tout segment semi-ouvert inclus dans l'intérieur relatif de , ;
- a pour épigraphe l'adhérence de l'épigraphe de .
La fonction est appelée la fermeture de . Les fonctions convexes égales à leur fermeture sont appelées des fonctions convexes fermées ; dit autrement ce sont les fonctions convexes dont l'épigraphe est fermé, ou encore autrement dit ce sont les fonctions convexes semi-continues inférieurement[27].
Fonction à valeurs vectorielles
On peut aussi introduire une notion de convexité pour les fonctions à valeurs vectorielles, pourvu que l'on se donne un cône dans l'espace d'arrivée de la fonction.
De façon plus précise, on suppose donnés deux espaces vectoriels et , un convexe de , un cône pointé convexe de et une fonction de dans . On dit que est -convexe si, pour tous et de et tout dans , on a :
Par les propriétés supposées de , l'ensemble des fonctions -convexes est un cône convexe de l'ensemble des fonctions de dans (parce que est un cône convexe), contenant les fonctions affines (parce que est pointé).
Si le cône est également saillant, il induit sur un ordre partiel, noté et défini par :
Alors, l'expression ci-dessus de la -convexité de s'écrit aussi :
ce qui rappelle l'inégalité de convexité familière.
Applications en physique
L'analyse convexe trouve un grand nombre d'applications en physique, lorsque les potentiels énergétiques sont localement convexes (existence de solutions stables, de changements de phase). En homogénéisation, par exemple, les théories de type variationnel permettent d'estimer les solutions d'équations aux dérivées partielles elliptiques grâce à la représentation des potentiels énergétiques par transformée de Legendre. La transformée de Legendre, formulation mathématique qui représente une fonction convexe par l'ensemble de ses tangentes, permet le développement de méthodes de linéarisation[28].
Notes et références
- Démontré p. 179 de J. L. W. V. Jensen, « Sur les fonctions convexes et les inégalités entre les valeurs moyennes », Acta Mathematica, vol. 30, , p. 175-193 (DOI 10.1007/BF02418571, lire en ligne).
- (en) Emil Artin, The Gamma Function, Dover, (1re éd. 1964), 48 p. (lire en ligne), p. 5.
- Une hypothèse de ce type est indispensable, car toutes les solutions de l'équation fonctionnelle de Cauchy satisfont .
- Ce résultat est attribué à Jensen par (en) Constantin Nicolescu et Lars-Erik Persson (en), Convex Functions and their Applications : A Contemporary Approach, Springer, coll. « Ouvrages de mathématiques de la Société mathématique du Canada » (no 23), (ISBN 978-0-387-24300-9, lire en ligne), p. 10. Ils renvoient à Jensen 1906, qui démontre directement une inégalité plus générale (voir infra).
- Artin 2015, p. 6. Pour une autre méthode, voir Nicolescu et Persson 2006, ou la Propriété 11 de .
- Démonstration de .
- Jensen 1906, p. 180, repris dans Artin 2015, p. 6.
- Ce résultat est cité par Nicolescu et Persson 2006, p. 20-21, qui l'attribuent à L. Galvani, renvoyant à son article « Sulle funzioni convesse di una o due variabili, definite in un aggregato qualunque », Rend. Circ. Mat. Palermo, vol. 41, 1916, p. 103-134 DOI 10.1007/BF03018290.
- On trouve une démonstration dans Artin 2015, p. 1 et 6, ou dans .
- Voir Nicolescu et Persson 2006, p. 21, qui attribuent les deux premiers points à Otto Stolz, renvoyant à son traité Grundzüge der Differential und Integralrechnung, vol. 1, Teubner, Leipzig, 1893.
- artin 2015, p. 4.
- Cf. Propriété 13 et Théorème 1 de .
- Énoncé dans Jacques Douchet, Analyse : recueil d'exercices et aide-mémoire, vol. 1, PPUR, , 3e éd. (1re éd. 2003) (lire en ligne), p. 77 (prop. 5.44) et démontré dans cet . Pour une généralisation aux fonctions convexes d'une variable vectorielle, voir (en) Jean-Paul Penot, Calculus Without Derivatives, coll. « GTM » (no 266), (lire en ligne), p. 202-203.
- Cf. Théorème 2 de .
- (en) Stephen Boyd et Lieven Vandenberghe, Convex Optimization, Cambridge University Press, (lire en ligne), p. 110.
- Pour l'ensemble de cette sous-section, voir (en) Jean-Baptiste Hiriart-Urruty et Claude Lemaréchal, Fundamentals of Convex Analysis, Springer, coll. « Grundlehren Text Editions », (1re éd. 2001), 259 p. (ISBN 978-3-540-42205-1, lire en ligne), p. 74-76.
- Selon ce qu'en dit R. T. Rockafellar dans le CIM Bulletin.
- Cf. Propriétés 8 et 9 de ..
- (en) Werner Fenchel, Convex Cones, Sets, and Functions, Princeton University Press, (lire en ligne), p. 57.
- La proposition qui suit est énoncée dans Nicolescu et Persson 2006, p. 114 (sous l'hypothèse d'un espace normé, qui ne joue pas un rôle essentiel dans la preuve).
- R. Glowinski, J.-L. Lions et R. Trémolières, Analyse numérique des inéquations variationnelles, t. 1 : Théorie Générale, Premières Applications, Paris, Dunod-Bordas, , p. 61 et 63, Lemmes 1.1 et 1.2.
- Hiriart-Urruty et Lemaréchal 2004, p. 102-104, la minoration de la fonction convexe ayant été adaptée au vu de Nicolescu et Persson 2006, p. 119.
- Nicolescu et Persson 2006, p. 137.
- Ces remarques sont disponibles, avec leurs preuves et quelques détails, dans Nicolescu et Persson 2006, p. 22.
- L'exemple figure dans Hiriart-Urruty et Lemaréchal 2004, p. 105, avec l'explication de la convexité de .
- Ce théorème est cité sans démonstration par Nicolescu et Persson 2006, p. 123, qui renvoient à (en) D. Gale, V. Klee et R. T. Rockafellar, « Convex functions on convex polytopes », Proc. Amer. Math. Soc., vol. 19, , p. 867-873.
- Pour l'ensemble de cette sous-sous-section, voir Hiriart-Urruty et Lemaréchal 2004, p. 79-80. Nicolescu et Persson 2006, p. 122, mentionnent également ces résultats en les attribuant à Fenchel 1951.
- Voir pour un aperçu (en) Ivar Ekeland et Roger Temam, Convex Analysis and Variational Problems, SIAM, , 402 p. (ISBN 978-0-89871-450-0, lire en ligne), chap. IV.
Voir aussi
Articles connexes
Bibliographie
(en) R. Tyrrell Rockafellar, Convex Analysis, Princeton, Princeton University Press, , 451 p. (ISBN 978-0-691-01586-6, lire en ligne)


![{\displaystyle [AB]}](https://img.franco.wiki/i/13e80b9404482bdbe7fe18d8435b3dd42fd39bb0.svg)




![{\displaystyle [0;1]}](https://img.franco.wiki/i/bc3bf59a5da5d8181083b228c8933efbda133483.svg)

![{\displaystyle ]0;1[}](https://img.franco.wiki/i/648c338a660699ded363552f4f2099cdefb02a35.svg)







![{\displaystyle [A_{1},A_{2}]}](https://img.franco.wiki/i/0f68119c675510a91737f3b1d6188a1c877d62bb.svg)






































































![{\displaystyle [A,B]\subset C}](https://img.franco.wiki/i/0ac3d6940299dc7513e9a6c1bd080c49f3dcdfed.svg)
![{\displaystyle t\in [0;1]}](https://img.franco.wiki/i/96a49ca7444bf740c79e71e58ad94040e59a09a6.svg)


















![[-1;1]](https://img.franco.wiki/i/c8bc389ca678dffbedd0d41ca0fecb9806c9b7cf.svg)
















![{\displaystyle t\in ]0;1[}](https://img.franco.wiki/i/80c0a6dee54d8107c15947fa00ccf25c6aac771b.svg)

![g_\beta:[0,2\beta]\to\R_+](https://img.franco.wiki/i/d1c6cfb200a9f48ad452b01939ac53ab0150f323.svg)












![{\displaystyle [x_{1},x_{1}']}](https://img.franco.wiki/i/89fc1349569081ec4c24dcef06c46cff4d10d5df.svg)












![[x'_1,x_2]](https://img.franco.wiki/i/3d85e67a8ea1aea339393fb03693848fe8a8be7a.svg)
![{\displaystyle [x_{1},x_{2}']}](https://img.franco.wiki/i/ff2901013559e15e40d43a92d95eded55c4b82e4.svg)


![[a,b]](https://img.franco.wiki/i/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)












![{\displaystyle ]x,z]}](https://img.franco.wiki/i/4d1b73302c0520e7d652b7c45804f9b1cbc8beb5.svg)
![f(x)=\lim_{\stackrel{y\to x}{y\in]x,z]}}f(y)](https://img.franco.wiki/i/355eabdb22d758ec4a836a34cb7b1823aa54fbde.svg)








