Fonction exponentielle
En mathématiques, la fonction exponentielle est la fonction notée exp qui est égale à sa propre dérivée et prend la valeur 1 en 0. Elle est utilisée pour modéliser des phénomènes dans lesquels une différence constante sur la variable conduit à un rapport constant sur les images. Ces phénomènes sont en croissance dite « exponentielle ».
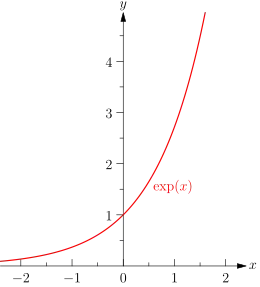
| Notation | |
|---|---|
| Réciproque | |
| Dérivée | |
| Primitives |
| Ensemble de définition | |
|---|---|
| Ensemble image |
| Valeur en zéro |
1 |
|---|---|
| Limite en +∞ |
+∞ |
| Limite en −∞ |
0 |
| Asymptotes |
|---|
On note e la valeur de cette fonction en 1. Ce nombre e qui vaut approximativement 2,71828 s'appelle la base de la fonction exponentielle et permet une autre notation de la fonction exponentielle :
- .
La fonction exponentielle est la seule fonction continue sur ℝ qui transforme une somme en produit et qui prend la valeur e en 1. C'est un cas particulier des fonctions de ce type appelées exponentielles de base a.
On peut la déterminer comme limite de suite ou à l'aide d'une série entière.
C'est la bijection réciproque de la fonction logarithme népérien.
Ces diverses définitions permettent d'étendre la définition de la fonction exponentielle à des fonctions de ℂ vers ℂ* ou même à des espaces plus compliqués et s'utilise alors en géométrie riemannienne, dans la théorie des groupes de Lie, ou encore dans l'étude des algèbres de Banach.
Les applications élémentaires des fonctions exponentielles réelles ou complexes concernent la résolution des équations différentielles, la mise en place de la théorie de Fourier… mais les champs d'applications des fonctions exponentielles sont extrêmement vastes : étude de la croissance des groupes, etc.
On appelle aussi parfois fonction exponentielle toute fonction dont l'expression est de la forme f(x) = Aeλx.
Fonction exponentielle réelle
Définitions
Il existe plusieurs points d'entrée possibles pour la définition de la fonction exponentielle : par la propriété de sa dérivée (la dérivée est égale à la fonction), par ses propriétés algébriques (elle transforme une somme en produit), ou par son développement en série.
Par une équation différentielle
Définition — On appelle fonction exponentielle l'unique fonction dérivable solution du problème de Cauchy suivant :
Cette propriété d'être sa propre dérivée se traduit par une propriété sur la sous-tangente à la courbe représentative de exp. La sous-tangente, c'est-à-dire la distance qui sépare le réel x de l'abscisse du point d'intersection de la tangente à la courbe au point d'abscisse x avec l'axe des x, est constante et vaut 1. On montre de plus que f ne s'annule jamais.
À partir de la fonction logarithme népérien
Définition — La fonction exp, de ℝ dans ℝ*
+, est la bijection réciproque de la fonction logarithme népérien.
En effet, la fonction logarithme népérien étant continue strictement croissante sur son ensemble de définition, et de limites infinies aux bornes, elle définit une bijection de ℝ*
+ sur ℝ. Sa réciproque est une fonction f définie sur ℝ vérifiant f(0) = 1 car ln(1) = 0. La fonction ln étant dérivable et de dérivée non nulle, sa réciproque est une fonction dérivable et, pour tout réel x,
Caractérisation algébrique
La propriété algébrique de la fonction exponentielle (fonction continue non nulle transformant une somme en produit) est partagée par un ensemble de fonctions qui portent aussi le nom de fonctions exponentielles. Elles sont entièrement déterminées dès que l'on a précisé leur valeur en 1 qui doit être un réel strictement positif. La fonction qui prend la valeur a en 1 est alors appelée fonction exponentielle de base a. On peut ainsi considérer que la fonction exponentielle est la fonction exponentielle de base e.
Définition — La fonction exp est l'unique fonction continue de ℝ dans ℝ* transformant une somme en produit, c'est-à-dire vérifiant l'équation fonctionnelle
et prenant la valeur e en 1.
On détermine exp(x) sur les entiers puis sur les rationnels puis sur les irrationnels par continuité. On démontre à partir de cette définition (voir l'article détaillé) que la fonction exp est non seulement continue mais dérivable et égale à sa propre dérivée. On retrouve ainsi la définition ci-dessus de l'exponentielle par une équation différentielle.
Il est possible de s'affranchir de la nécessité de connaître au préalable e par la caractérisation suivante:
Caractérisation — La fonction exp est l'unique fonction dérivable de ℝ dans ℝ* transformant une somme en produit, c'est-à-dire vérifiant l'équation fonctionnelle
et dont la dérivée prend la valeur 1 en 0.
On s'inspire de l'égalité pour tous entiers q > 0 et p pour introduire une nouvelle notation pour la fonction exp : pour tout réel x.
Toutes les fonctions exponentielles de base a s'expriment à l'aide de la fonction exp et de la fonction logarithme népérien :
Par une série
Enfin, en appliquant la méthode de recherche de solutions analytiques des équations différentielles linéaires, on peut définir l'application exponentielle exp ou encore x ↦ ex comme la somme d'une série entière de rayon de convergence infini :
où n! est la factorielle de n.
C'est également cette série qu'on obtient en appliquant la démonstration du théorème de Cauchy-Lipschitz[2] - [3] - [4], c'est-à-dire en construisant la solution exp de l'équation différentielle comme limite de la suite de fonctions (un) définie par u0 = 1 et
On déduit de cette série entière l'un des nombreux développements en fraction continue généralisée de la fonction exponentielle :
Une analyse détaillée d'expressions de cette nature est proposée dans l'article « Approximant de Padé de la fonction exponentielle ».
Étude de la fonction exponentielle
La fonction exp prend en 1 une valeur notée e, qui vaut environ 2,718 et est un nombre transcendant.
La première des quatre définitions équivalentes ci-dessus montre que la fonction exp est de classe C∞. La dernière montre qu'elle est même analytique.
Chacune des trois premières montre que la fonction exp est strictement croissante de ℝ dans ℝ*+ et que
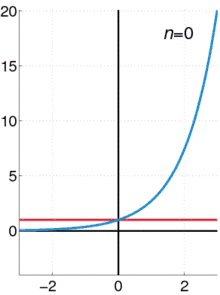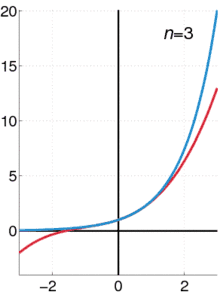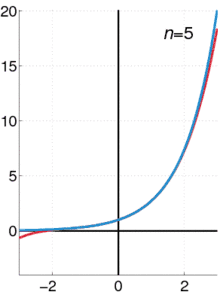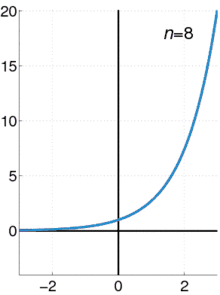
Plus précisément — voir l'article « Indétermination de la forme ∞/∞ » — la fonction exp tend vers + ∞ plus rapidement que toute fonction polynomiale quand sa variable tend vers + ∞, c'est-à-dire que
quel que soit l'entier naturel n. Par changement de variable, on en déduit
La croissance de exp peut se déduire de la positivité de sa dérivée exp. De même, puisque sa dérivée seconde exp est strictement positive, la fonction exp est strictement convexe.
Propriétés
La fonction exponentielle, de ℝ sur ℝ*+, est la bijection réciproque de la fonction logarithme népérien : pour tous réels y > 0 et x,
- ln(ex) = x, eln(y) = y et ex = y ⇔ x = ln(y).
La fonction exponentielle transforme les sommes en produits, c'est-à-dire que pour tous réels x et y, ex + y = exey.
On en déduit que pour tout réel x et tout rationnel b, (ex)b = ebx.
Pour b irrationnel, cette équation peut tenir lieu de définition, c'est-à-dire que l'une des façons de définir l'exponentielle de base a est de poser, pour tous réels a > 0 et b : ab = ebln(a).
Généralisation à d'autres ensembles
Définitions
On peut définir la fonction exp complexe de deux façons :
- En utilisant la propriété :,on écrit où a et b sont des nombres réels.
La fonction exponentielle complexe s'exprime donc à l'aide de la fonction exponentielle réelle et des fonctions trigonométriques. - En utilisant le développement en série de l'exponentielle, on étend celle-ci au plan complexe :
La fonction exponentielle vérifie alors les propriétés importantes suivantes :
- pour tous z et w,
- la fonction exponentielle dans le plan complexe est une fonction holomorphe et sa dérivée (au sens complexe) est elle-même :
Ces formules se montrent à l'aide des formules de trigonométrie ou à l'aide de la notion de produit de Cauchy de deux séries, selon le mode de définition de l'exponentielle.
C'est une fonction périodique, de période le nombre imaginaire pur 2iπ. Cette périodicité entraînant la non-injectivité, prolonger le logarithme naturel à l'ensemble des nombres complexes donne naturellement une fonction multiforme z ↦ ln(z), appelée logarithme complexe.
L'exponentielle plus générale : pour tous nombres complexes z et w, est alors aussi une fonction multiforme. Les propriétés ci-dessus des exponentielles restent vraies à condition de les interpréter convenablement comme des relations entre fonctions multiformes.
La fonction exponentielle complexe transforme l'axe imaginaire pur en le cercle unité. C'est la fonction que l'on utilise pour montrer que la droite réelle est un revêtement du cercle unité.
Représentations
Si on peut représenter graphiquement, dans l'espace, les fonctions , , et
- Surfaces représentant la partie réelle, la partie imaginaire, le module et l'argument principal de l'exponentielle complexe
.png.webp)
.png.webp)


- Courbe de densité représentant la partie réelle et la partie imaginaire de l'exponentielle complexe
_Density.png.webp)
_Density.png.webp)
- Pour d'autres représentations de l'exponentielle complexe, se référer à .
Exponentielle d'une matrice
La définition de l'exponentielle comme série entière permet de définir l'exponentielle d'une matrice carrée M comme
- .
Les exponentielles de matrices sont utiles dans la résolution des équations différentielles linéaires.
Exponentielle d'un opérateur différentiel
On peut de même définir l'exponentielle d'un opérateur différentiel D par :
- .
Par exemple, quand où a est une constante :
- ,
si bien que pour toute fonction f(x) analytique, on a
- ,
un avatar de la formule de Taylor[5].
Exponentielle dans un groupe additif
La définition de l'exponentielle comme un morphisme continu d'un groupe additif vers un groupe multiplicatif permet de définir une fonction exponentielle de ℝ vers tout groupe topologique. Plus généralement, pour un groupe topologique G, on appelle sous-groupe à un paramètre tout morphisme continu ℝ → G. Certains ouvrages peuvent remplacer l'hypothèse de continuité par la mesurabilité.
Exponentielle dans une variété différentielle
La définition de la fonction exponentielle comme solution d'une équation différentielle se généralise pour les groupes de Lie et les géodésiques dans les variétés riemanniennes
Exponentielle dans une algèbre de Banach
La définition de l'exponentielle comme série entière permet de la définir sur des algèbres de Banach (voir l'article Calcul fonctionnel).
Applications
Équation différentielle linéaire
L'importance majeure des fonctions exponentielles en sciences, provient du fait qu'elles sont proportionnelles à leur propre dérivée. a étant un nombre réel ou complexe, on a :
ou plus exactement, la fonction est l'unique solution de l'équation fonctionnelle
Si une grandeur croît ou décroît, en fonction du temps et que la vitesse de «sa course» est proportionnelle à «sa taille», comme dans le cas de la croissance d'une population, des intérêts composés continus ou de la décroissance radioactive, alors cette grandeur peut être exprimée comme une constante fois une fonction exponentielle du temps.
La fonction exponentielle de base e est solution de l'équation différentielle élémentaire :
et on la rencontre fréquemment dans les solutions d'équations différentielles. En particulier, les solutions d'une équation différentielle linéaire peuvent être écrites à l'aide des fonctions exponentielles. On les trouve aussi dans les solutions des équations différentielles de Schrödinger, de Laplace ou dans l'équation différentielle du mouvement harmonique simple.
Fonction trigonométrique
La fonction exponentielle est d'une utilité capitale en trigonométrie. Les formules d'Euler (que l'on démontre à partir de la définition exp(i z) = cos z+ i sin z) nous donnent un lien direct entre les fonctions cosinus et sinus, réelles ou non, et la fonction exponentielle complexe.
Ces formules permettent de retrouver la plupart des identités trigonométriques, en particulier
à partir desquelles on peut retrouver quasiment toutes les autres.
La fonction exponentielle est aussi un moyen facile de linéariser les expressions de la forme cospx sinqx : voir le § « Linéarisation » de l'article sur les identités trigonométriques.
La fonction exponentielle trouve aussi son utilité quand on veut démontrer la formule de Moivre.
Fonction exponentielle et trigonométrie hyperbolique
À partir de la fonction exponentielle, on peut définir les fonctions de trigonométrie hyperbolique, définissant les fonctions hyperboliques cosinus hyperbolique, cosh et sinus hyperbolique, sinh, utilisées en partie dans les résolutions des équations différentielles de second ordre.
Théorie de Fourier
Les fonctions exponentielles où t est un réel et k un entier relatif sont utilisées dans la théorie de Fourier. Elles permettent d'exprimer toute fonction périodique comme somme de fonctions trigonométriques, ce sont les séries de Fourier. Elles permettent aussi de définir la transformée de Fourier d'une fonction de carré sommable.
Fonction sigmoïde
La fonction sigmoïde pour tout réel est particulièrement utile dans les réseaux de neurones pour calculer le gradient de l'erreur.
Notes et références
- Voir cet . Pour d'autres démonstrations (plus compliquées), voir par exemple celles de G. Costantini ou de Perrin 2002.
- T. Budzinski, « Théorème de Cauchy-Lipschitz », sur le serveur des élèves de l'ENS, .
- « Autour de la fonction exponentielle et ses constructions », sur OpenClassrooms.
- (en) Foster Morrison, The Art of Modeling Dynamic Systems : Forecasting for Chaos, Randomness and Determinism, Dover, (lire en ligne), p. 217 élargit cette remarque aux fonctions t ↦ exp(t – t0) et Roger Godement, Analyse mathématique, vol. 3, Springer, (lire en ligne), p. 273, aux exponentielles matricielles.
- Jean-Pierre Provost et Gérard Vallée, Les maths en physique : La physique à travers le filtre des mathématiques, Paris, Éditions Dunod, coll. « Sciences Sup », , 1re éd., 331 p. (ISBN 2-10-004652-7), p. 7.
Voir aussi
Articles connexes
Liens externes
- « Fonction exponentielle : à tout Euler », La Méthode scientifique, France Culture, 19 novembre 2020.
- Daniel Perrin, « Une définition de la fonction exponentielle dans l'esprit des nouveaux programmes »,
- Jean-Pierre Demailly, Puissances, exponentielles, logarithmes de l'école primaire jusqu'à la terminale, 2010









































![{\displaystyle z^{w}=\exp[w\ln(z)]}](https://img.franco.wiki/i/c07c7fd78e9d43de9c096495ff2ec56f298b173b.svg)


























