Fonction carré
En analyse réelle, la fonction carré[1] est la fonction qui associe à chaque nombre réel son carré, c’est-à-dire le résultat de la multiplication de ce nombre par lui-même.
| Notation | |
|---|---|
| Réciproque |
sur |
| Dérivée | |
| Primitives |
| Ensemble de définition | |
|---|---|
| Ensemble image | |
| Parité |
paire |
| Valeur en zéro |
0 |
|---|---|
| Limite en +∞ |
+∞ |
| Limite en −∞ |
+∞ |
| Minima |
0 |
| Zéros |
0 |
|---|---|
| Points fixes |
0 ; 1 |
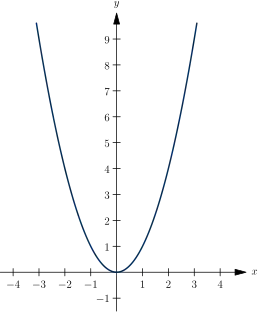
Cette fonction puissance, qui peut s’exprimer sous la forme x ↦ x2 = x × x est une fonction paire, positive et dont la courbe est une parabole d’axe vertical, de sommet à l’origine et orientée dans le sens des ordonnées positives. Comme fonction continue et strictement croissante sur l’intervalle [0, +∞[, elle induit une bijection de cet intervalle dans lui-même, admettant pour réciproque la fonction racine carrée.
La fonction carré est aussi le premier exemple de fonction du second degré, et se généralise à plusieurs variables avec la notion de forme quadratique. Elle s’étend également au plan complexe comme une fonction entière avec une racine double en 0.
Propriétés
Signe
La première propriété est la positivité (au sens large) de la fonction carré. En effet pour tout réel x, le réel x × x est le produit de deux nombres réels de même signe ; par la règle des signes il est donc positif.
Parité
La fonction est paire : f(x) = f(–x) pour tout réel x. En effet, (–x) × (–x) = x × x.
Convexité
La fonction carré est strictement convexe sur . En effet, sa dérivée seconde est strictement positive : f '' = 2 > 0.
Résolution d'équation de type x2 = a
Calculer les antécédents d'un réel a par la fonction carré équivaut à résoudre l'équation x2 = a. Il y a trois cas possibles :
- a < 0 : aucune solution dans l'ensemble des réels ;
- a = 0 : une solution, x = 0 ;
- a > 0 : deux solutions, √a et –√a.
Par exemple, les solutions de x2 = 9 sont 3 et –3.
On peut également déterminer les antécédents graphiquement : les antécédents de a sont les abscisses des points d'intersection de la droite d'équation y = a et du graphe de la fonction carré.
Dérivée
La dérivée de la fonction carré est (c'est une fonction linéaire donc impaire)[2]. Elle est donc (strictement) négative sur et positive sur , si bien que la fonction carré est (strictement) décroissante sur ]–∞ , 0] et croissante sur [0, +∞[. Elle s'annule en 0, son minimum global. Le sens de variation de la fonction carré est à prendre en compte lors de la résolution d'inéquations (inversion des inégalités si les valeurs sont négatives).
Intégrale
Comme la fonction carré est un polynôme quadratique, la méthode de Simpson est exacte lorsqu'on calcule son intégrale. Pour tout polynôme quadratique P et a et b réels, on a :
donc pour la fonction carré définie par , on a :
Primitive
La fonction carré possède comme primitives toutes les fonctions gC définies par, pour C une constante réelle arbitraire :
- .
Représentation graphique
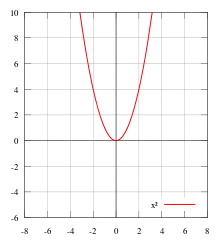
Dans un repère orthonormal, la fonction est représentée par une parabole dont le sommet est le point (0, 0). L'intégralité de la parabole se situe au-dessus de l'axe des abscisses — ce qui traduit la positivité de la fonction — et la parité est décelable grâce à l'axe de symétrie qu'est l'axe des ordonnées.
La limite de la fonction carré, en plus l'infini et en moins l'infini, est égale à plus l'infini.
Extension au domaine complexe
On peut étendre la définition de la fonction carré au domaine complexe en définissant . Par exemple, si , . peut être aussi considérée comme une fonction de dans , la fonction qui au couple associe le couple puisque, en écrivant , on a[3] .
La fonction carré peut servir à illustrer des propriétés de différentiabilité, d'holomorphie, sert souvent d'exemple pour illustrer les conditions de Cauchy-Riemann[4] - [5].
La fonction carré sert également à démontrer une propriété géométrique des triplets pythagoriciens.
La fonction carré sert également[6] à illustrer le théorème de l'application conforme.
Notes et références
- Le terme carré est ici le nom de la fonction et non un adjectif qualificatif pour le nom fonction. Il ne s’accorde donc pas en genre.
- Voir par exemple ce .
- Murray R. Spiegel (en), Variables complexes : cours et problèmes, McGraw-Hill, (ISBN 2-7042-0020-3, OCLC 299367656), p. 41.
- Jacques Dixmier, Cours de mathématiques du premier cycle : deuxième année : exercices, indications de solutions, réponses, Gauthier-Villars, (ISBN 2-04-015715-8, OCLC 23199112), chap. 52.
- Michèle Audin, « Cours d'analyse complexe », sur irma.math.unistra.fr, ex II.18.
- Spiegel 1973, p. 42.











![{\displaystyle \int _{a}^{b}P(x)\,\mathrm {d} x={\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right]}](https://img.franco.wiki/i/bf5560c525268a05008056f9ae9c1823bc910e1d.svg)











