Extremum
Un extremum (pluriel extrema ou extremums), ou extrémum (pluriel extrémums), est une valeur extrême, soit maximum, soit minimum. Cette notion est particulièrement utilisée en mathématiques, où l'expression maximo-minimum, introduite par Nicolas de Cues, correspond à partir de Fermat et Leibniz aux extrêmes d'une courbe ou d'une fonction, repérés par le fait que les dérivées s'y annulent. Elle est aussi utilisée en physique, où le principe de moindre action est un principe extrémal ainsi que Euler l'a montré.
Généralités
En théorie des ensembles
Dans un ensemble ordonné E, un élément d'une partie A est le plus grand élément, ou maximum de A, s'il appartient à A et est supérieur à tout autre élément de A. L'existence d'un maximum n'est en général pas assurée pour toute partie d'un ensemble ordonné. En revanche, s'il existe, un tel élément est unique (ce qui justifie l'emploi de l'article défini « le » dans la définition). De manière analogue, le plus petit élément ou minimum est, s'il existe, un élément de A inférieur à tout autre élément de A.
Unicité
Si une partie A de E admet deux maxima, m1 et m2, alors m1 est plus grand que tout élément de A, donc en particulier que m2 ; et de même, m2 est plus grand que m1. Par antisymétrie des relations d'ordre, l'égalité m1 = m2 s'en déduit.
Comparaison avec d'autres notions
D'autres notions relatives aux ensembles ordonnés sont proches de celles de maximum ; les comparer permet de mieux les appréhender.
- La notion de majorant et de minorant : s'il existe, un élément de E est un majorant de A s'il est plus grand que tout élément de A ; s'il existe, un élément de E est un minorant de A s'il est plus petit que tout élément de A ; ainsi, les extremums (le maximum et le minimum) qui existent dans un ensemble E font partie (respectivement) des majorants et minorants de E dans lui-même.
- La notion de borne (borne supérieure, aussi appelée supremum, ou borne inférieure, aussi appelée infimum) : si elle existe, la borne supérieure de A est le plus petit de tous les majorants de A dans E (la borne supérieure de A est donc définie comme le minimum d'une certaine partie de E et son unicité est garantie mais pas son existence). A admet un maximum si et seulement si sa borne supérieure existe et appartient à A (et dans ce cas, elle est égale au maximum) ; et réciproquement pour la borne inférieure.
- La notion d'élément extrémal (élément maximal ou élément minimal) également appelée borne inclusive : un élément de E est maximal dans A, s'il appartient à A, et n'est inférieur à aucun autre élément de A ; un élément de E est minimal dans A, s'il appartient à A, et n'est supérieur à aucun autre élément de A.
S'ils existent, les extremums (le maximum ou le minimum) d'un ensemble E, sont toujours des éléments extrémaux (bornes inclusives : élément maximal ou élément minimal) de E dans lui-même ; les notions d'extremum (le maximum et le minimum) et d'élément extrémal (un élément maximal ou un élément minimal) coïncident dans les ensembles munis d'un ordre total ; lorsque E est fini, il y a équivalence entre l'existence d'un unique élément extrémal (borne inclusives : élément maximal ou élément minimal) et l'existence d'un extremum (le maximum ou le minimum, chacun nécessairement unique avec un ordre total sur un ensemble fini).
Mais ce n'est pas nécessairement vrai sur un ensemble vide ou infini ou dans le cas d'un ordre non total (où deux éléments peuvent être ordonnés de la même façon avec les autres et mutuellement entre eux, et peuvent donc chacun être des éléments extrémaux mais pourtant distincts). Par exemple l'ensemble de seulement trois entiers {0, 1, 2} muni de l'ordre partiel comparant non pas leur valeur mais leur parité (le reste de leur division euclidienne par 2) n'est pas totalement ordonné car les éléments 0 et 2 ont la même parité 0 (les éléments 0 et 2 sont des valeurs minimales pour cet ordre partiel, mais ils sont différents : cet ensemble ordonné n'a donc pas de minimum, mais il a un maximum avec l'élément 1). Dans le sous-ensemble {0, 2} avec le même ordre, il n'y a ni minimum, ni maximum, mais les valeurs minimales (de même les valeurs maximales) existent et forment ce même ensemble de deux éléments.
Quand l'ensemble ordonné est un singleton, son unique élément en est à la fois son maximum et son minimum. Dans le cas dégénéré où l'ensemble ordonné est vide, il n'y a aucun extremum, ni aucune valeur extrémale, et tout élément de n'importe quel ensemble (incluant donc l'ensemble vide comme une partie) en est à la fois un majorant et un minorant, et donc aussi une borne si cet autre ensemble est totalement ordonné.
Exemples
Dans l'ensemble N des entiers naturels muni de son ordre usuel, toute partie non vide admet un plus petit élément et toute partie majorée (c'est-à-dire admettant un majorant) est finie donc admet même un maximum. Par exemple N lui-même a pour minimum 0 et n'a pas de maximum.
Dans l'ensemble R des nombres réels muni de son ordre usuel, certaines parties majorées n'admettent pas de plus grand élément, par exemple l'intervalle ]0, 1[ des nombres strictement compris entre 0 et 1.
Dans R, les fonctions minimum et maximum d'une paire peuvent s'exprimer à l'aide de valeurs absolues :
Dans un ensemble ordonné muni d'un ordre non total, certaines parties admettent des éléments maximaux qui ne sont pas des maxima.
Par exemple dans l'ensemble E = {∅, {0}, {1}, {0, 1}} des parties de l'ensemble {0, 1}, ordonné par l'inclusion, la partie A = {∅, {0}, {1}} admet (un minimum et) deux éléments maximaux non comparables donc pas de maximum (seulement une borne supérieure : {0, 1}, qui n'appartient pas à A).
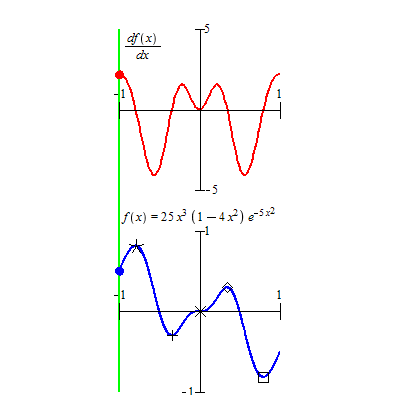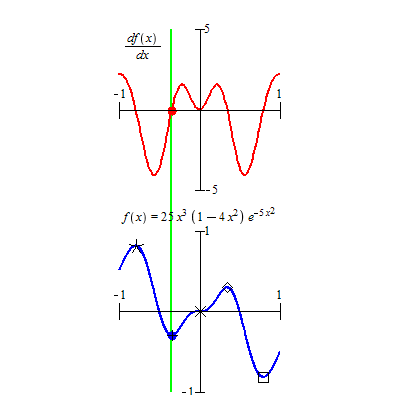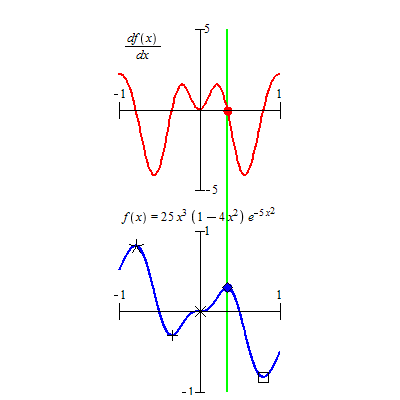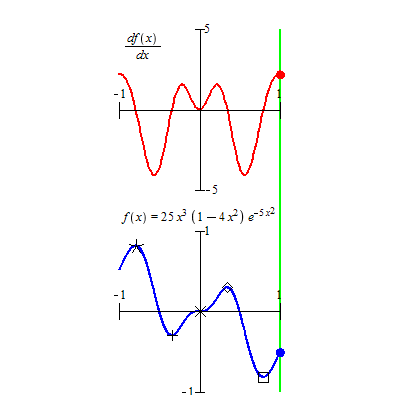
Extrema d'une fonction
Le maximum d'une fonction f définie sur un ensemble E et à valeurs dans un ensemble F ordonné est le maximum de l'ensemble des valeurs prises par f (de la partie f(E) de F). Ainsi m est le maximum de f s'il existe un élément a de E tel que f(a) = m et tel que pour tout élément x de E, f(x) ≤ f(a) ; l'élément a (qui n'est pas nécessairement unique) est appelé point de maximum de f.
Dans le cas où l'espace de départ de f est muni d'une structure topologique (par exemple si f est une fonction d'une ou plusieurs variables réelles à valeurs réelles), on distingue deux types d'extrema : les extrema globaux, qui correspondent à la définition précédente, et les extrema locaux.
Extremum local d'une fonction
Soient f une fonction définie sur un espace topologique E et a un point de E. On dit que f atteint en a un maximum local s'il existe un voisinage V de a tel que pour tout élément x de V, on ait f(x) ≤ f(a).
On dit alors que f(a) est un « maximum local » de f sur E et que a est un point de maximum local de f.
Lorsqu'il existe un voisinage V de a tel que pour tout élément x de V différent de a, on ait f(x) < f(a), on dit que f atteint en a un maximum local strict.
Lorsque E est une partie d'un espace métrique (par exemple d'un espace vectoriel normé, comme Rk), les voisinages de a dans ces définitions peuvent être choisis égaux à des boules. Par exemple : f atteint en a un maximum local s'il existe un réel ε > 0 tel que pour tout élément x de E à distance < ε de a, on ait f(x) ≤ f(a).
Théorèmes topologiques d'existence d'extrema globaux
Soit une fonction , où D est un espace topologique. Par exemple, D peut être une partie de R (cas d'une fonction d'une variable réelle), ou d'un espace Rk, avec k un entier naturel (cas d'une fonction de k variables réelles).
L'existence d'extrema globaux est assurée dès lors que la fonction f est continue et que la partie D est compacte : en effet, l'image f(D) est alors une partie compacte de l'espace d'arrivée R ; en tant que partie bornée de R, elle admet une borne supérieure, et cette borne supérieure est dans f(D) puisque cette partie est fermée.
En dimension k = 1, c'est en particulier le cas si I est un intervalle fermé borné, c'est-à-dire de la forme [a, b] (voir Théorème des bornes). En dimension supérieure k, c'est en particulier le cas si D est une boule fermée (de la forme , où désigne une norme sur Rk).
Méthodes issues du calcul différentiel pour la recherche d'extrema locaux
Soit une fonction , où U est un ouvert de Rk ; par exemple, dans le cas d'une variable réelle, U peut être un intervalle ouvert de la forme ]a, b[ (avec a et b des nombres réels, ou , ou ).
L'étude des extrema passe souvent par la recherche des zéros de la dérivée, appelés points critiques (ou points stationnaires) de f. Un point critique n'est pas nécessairement un point d'extremum, comme le montre l'exemple de la fonction au point 0. On peut cependant, sous certaines hypothèses supplémentaires, affirmer qu'un point critique est un point d'extremum.
Cas d'une fonction d'une variable
- Condition nécessaire pour un extremum local
Dans le cas d'une fonction dérivable f d'une seule variable, si f possède un extremum local en un point de l'ouvert de définition de f, alors la dérivée de f en ce point est nulle.
- Condition suffisante pour un extremum local
Si f est dérivable sur l'ouvert U et si, en un point , la dérivée de f s'annule en changeant de signe, alors f atteint un extremum local en . Plus précisément, en supposant :
- s'il existe un réel tel que
- et sur , sur ,
- alors f atteint un maximum local en ;
- s'il existe un réel tel que
- et sur , sur ,
- alors f atteint un minimum local en .
Cas d'une fonction de plusieurs variables
- Condition nécessaire pour un extremum local
Si la fonction f atteint un extremum local en un point a de U où elle est différentiable, alors toutes ses dérivées partielles s'annulent en a.
- Condition suffisante pour un extremum local
On suppose que f est deux fois dérivable en un point de U. Sa matrice hessienne en est notée , c'est-à-dire que ; d'après le théorème de Schwarz, cette matrice est symétrique.
- Si et si est définie négative, alors f atteint un maximum local strict en .
- Si et si est définie positive, alors f atteint un minimum local strict en .
- Cas d'une fonction de plusieurs variables avec contraintes
Les conditions d'optimalité de ces problèmes sont présentées dans « Conditions d'optimalité ».













![{\displaystyle [a-\alpha ,\,a+\alpha ]\subset U}](https://img.franco.wiki/i/9404756bef1cd0230ed0a2e34460cee59b884527.svg)

![[a-\alpha,\, a]](https://img.franco.wiki/i/c6756e12c2134db1419bbbb8bf958cdf1aad14ce.svg)

![[a,\, a + \alpha]](https://img.franco.wiki/i/51e1c0fa3781b21b1dcc78e49ca7e68c3b96cbb5.svg)


