Ellipse de Steiner
En géométrie, l’ellipse de Steiner d'un triangle est l'unique ellipse tangente à chacun des côtés en leur milieu. Elle est nommée en référence au mathématicien suisse Jakob Steiner.
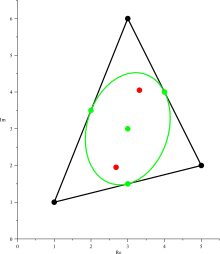
Démonstration
Dans le cas où le triangle est équilatéral, cette ellipse est le cercle inscrit. Comme tout autre triangle est l'image d'un triangle équilatéral par une application affine, l'image du cercle inscrit par une telle application est une ellipse qui satisfait les conditions de tangence au milieu de chaque côté.
Cette démonstration est analogue à celle du théorème des cinq points, qui fait intervenir également des conditions de tangence et d'incidence. En réalité, les six conditions requises pour l'ellipse de Steiner sont liées par la donnée du triangle initial.
Propriétés
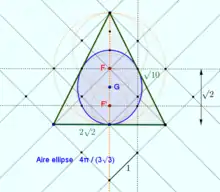
- L'ellipse coupe chaque médiane du triangle au tiers de sa longueur. Ceci permet une construction de l'ellipse avec six points.
- Parmi toutes les ellipses inscrites dans le triangle, l'ellipse de Steiner est celle qui a une aire maximale. Le rapport de l'aire de l'ellipse sur celle du triangle est égal à .
- Le centre de l'ellipse est l'isobarycentre du triangle.
- Si z1, z2 et z3 sont les affixes complexes des sommets du triangle et si P(z) est le polynôme (z – z1)(z – z2)(z – z3), alors les foyers de l'ellipse sont les deux racines du polynôme P', dérivé du polynôme P. C'est le théorème de Marden.
- Les foyers sont conjugués isogonaux par rapport au triangle[1] .
- La droite passant par les deux foyers de l'ellipse est la droite telle que la somme des carrés des distances des sommets du triangle à la droite soit minimale (droite de régression orthogonale des trois sommets).
- L'ellipse recoupe le cercle d'Euler (en plus des pieds des médianes) au point X115 (Nombre de Kimberling) milieu du segment reliant les deux points de Fermat. La tangente en X115 à l'ellipse est médiatrice de ce segment.
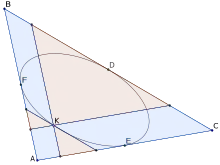
- Soit K un point de l'ellipse de Steiner d'un triangle ABC. Si on trace par K les parallèles aux côtés du triangle, celles-ci découpent ABC en petits triangles et parallélogrammes. La somme des aires des petits triangles (en bleu sur la figure) est égale à la somme des aires des parallélogrammes (en beige)[2].
Généralisation
Plus généralement, dans un triangle (ABC), si A', B' et C' sont des points respectivement situés sur les segments [BC], [AC] et [AB], alors il existe une ellipse passant par A', B' et C' et tangente en chacun de ces points à un côté du triangle si et seulement si les droites (AA'), (BB') et (CC') sont concourantes ; dans ce cas, l'ellipse obtenue est unique.
Ce type d'énoncé se modifie en choisissant des points de tangence sur les droites supportant les côtés du triangle, les coniques obtenues pouvant alors être des hyperboles ou paraboles.
Bibliographie
- Yves Ladegaillerie, Géométrie pour le Capes et l'Agrégation, chapitre 8, exercice 3.4.7.
- D. Minda, S. Phelps, Triangles, ellipses and cubic polynomials, Amer. Math. Monthly, 115, n°8 (), 679-689.
- J. Steiner, « Géométrie pure. Développement d’une série de théorèmes relatifs aux sections coniques », Ann.Math. Pures Appl, no 19, 1828/1829, p. 37–64.
Notes et références
- (en) Beniamin Bogosel, « A Geometric Proof of the Siebeck–Marden Theorem », Amer. Math. Monthly, vol. 125, no 4, , p. 459-463 (DOI 10.4169/amer.math.monthly.124.5.459)
- (en) A. Eydelzon, « On a New Property of the Steiner Inellipse », Amer. Math. Monthly, vol. 127, no 10, , p. 933-935 (DOI 10.1080/00029890.2020.1820795)
Articles connexes
- Coniques circonscrites et inscrites à un triangle
- Ellipsoïde de John (en)
