Cercle inscrit
En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone. De manière plus générale, on parle de cercle inscrit dans une surface bornée pour indiquer un cercle de plus grand rayon possible inclus dans la surface. Un polygone ayant un cercle inscrit est dit circonscriptible.
Existence
Pour qu'un polygone possède un unique cercle inscrit, il faut que ses bissectrices soient concourantes. Si c'est le cas, le point d'intersection est le centre du cercle inscrit.
Cas particuliers
Triangle
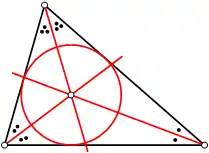
Tout triangle non plat possède un unique cercle inscrit.
Quadrilatère
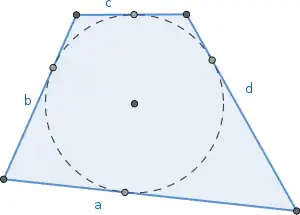
Un quadrilatère pour lequel il existe un cercle inscrit est dit circonscriptible ou tangentiel ; les losanges et les carrés sont toujours circonscriptibles.
Le théorème de Pitot permet de caractériser les quadrilatères tangentiels.
Bibliographie
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
- Méthodes modernes en géométrie de Jean Fresnel
- Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)