Théorème de Marden
En mathématiques, le théorème de Marden, portant le nom du mathématicien Morris Marden, établit une relation géométrique entre les zéros d'un polynôme du troisième degré d'une variable complexe et les zéros de son polynôme dérivé :
- Si les zéros z1, z2, z3 d'un polynôme du troisième degré à coefficients complexes ne sont pas alignés, alors il existe une unique ellipse inscrite dans le triangle de sommets z1, z2, z3 et tangente aux côtés du triangle en leur milieu. Cette ellipse est appelée ellipse de Steiner. Le théorème assure alors que les foyers de cette ellipse sont les zéros du polynôme dérivé de .
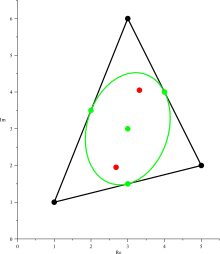
Le théorème de Marden
Marden attribue ce théorème à Jörg Siebeck[1] et rapporte neuf versions de ce théorème parues entre 1864 et 1928.
Notes et références
- (de) Jörg Siebeck, « Ueber eine neue analytische Behandlungsweise der Brennpunkte », Journal für die reine und angewandte Mathematik, vol. 64, , p. 175-182
Sources
- (en) Dan Kalman, « An Elementary Proof of Marden's Theorem] », American Mathematical Monthly, vol. 115, no 4, , p. 330-338 (lire en ligne)
- (en) D. Minda et S. Phelps, « Triangles, ellipses, and cubic polynomials », American Mathematical Monthly, vol. 115, no 8, , p. 679-689 (lire en ligne)
- (en) Morris Marden, Geometry of Polynomials, Providence, AMS,
Articles connexes
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.
