Point de Fermat
En géométrie euclidienne, le point de Fermat d'un triangle ABC donné est le point F du plan pour lequel la somme FA + FB + FC des distances aux trois sommets du triangle est minimale.
Il porte ce nom en l'honneur du mathématicien français Pierre de Fermat qui l'évoque dans un de ses ouvrages. Il est également appelé point de Torricelli ou premier point isogonique, ou point de Steiner.
Énoncé du théorème
Théorème et définition du point de Fermat — Pour tout triangle non aplati ABC, la somme MA + MB + MC des distances d'un point M du plan aux trois sommets est minimale en un point F unique appelé point de Fermat du triangle.
Si les angles du triangle sont strictement inférieurs à 120°, le point de Fermat est l'unique point F tel que .
Si l'un des angles du triangle ABC est supérieur ou égal à 120°, le point de Fermat est le sommet correspondant à cet angle.
L'existence du point F est assurée par le fait que la fonction définie sur le plan par est continue et tend vers l'infini en l'infini, et son unicité par le fait que cette fonction est strictement convexe.
Historique
En 1636, Fermat pose à la fin de son écrit Méthode du maximum et du minimum le problème suivant[1]: « Étant donnés trois points, en trouver un quatrième tel que la somme de ses distances aux trois points donnés soit minima » mettant au défi quiconque de trouver une méthode plus efficace pour le résoudre que la méthode du maximum qu'il vient de mettre au point. Evangelista Torricelli lui fournit une solution géométrique du problème vers 1640[2]. Utilisant les propriétés géométriques des ellipses, il démontre que le point doit être situé sur les trois cercles circonscrits aux triangles équilatéraux construits autour du triangle, cercles que l'on appelle en son honneur cercles de Torricelli. Bonaventura Cavalieri publie en 1647 dans son livre Exercitationes Geometrica sex [3], une solution complète incluant le cas où un angle du triangle excède 120°. Cependant leurs démonstrations indiquent la seule position possible d'un minimum et ne prouvent pas l'existence de celui-ci, existence qui leur semble acquise[4]. Cette existence résulte de la continuité de la fonction qui à tout point M associe la somme des distances à trois points fixes, mais un tel argument était inconnu au XVIIe siècle. En 1659, Vincenzo Viviani produit une autre solution[5] au problème utilisant un lemme qui porte aujourd'hui le nom de théorème de Viviani[6]. Thomas Simpson, en 1750, prouve qu'il est possible de trouver le point de Fermat en prenant le point d'intersection du cercle de Torricelli avec la droite joignant le sommet du triangle n'appartenant pas au cercle au sommet du triangle équilatéral qui lui est opposé[7]. Une telle droite est appelée droite de Simpson en son honneur[8]. Il généralise le problème à plusieurs points[9] ainsi qu'à des sommes pondérées[10]. En 1834[11], Franz Heinen démontre, à l'aide du théorème de Ptolémée, que la longueur des segments définis par Simpson est égale à la somme minimale recherchée[8].
L'existence du point de Fermat correspond au théorème de Schruttka[12] (aussi connu sous le nom de théorème de Torricelli, ou théorème de Fermat).
Le problème est popularisé par Richard Courant et Herbert Robbins en 1941 dans leur livre Qu'est-ce que les mathématiques ?. Leur présentation du problème n'est pas exempte d'erreurs selon Boltyanski et al.[13]. En particulier, ils baptisent ce problème du nom de Steiner au lieu de l'attribuer à Fermat. Jakob Steiner a effectivement travaillé sur un problème voisin en théorie des arbres, problème portant le nom d'arbre de Steiner : « un réseau étant donné, connectant n points. Quel est le réseau de longueur minimale conservant la connexion entre les n points ? »
Plusieurs généralisations du problème ont été envisagées : augmentation du nombre de points, pondération de la somme, élévation des distances à la puissance n, travail dans des espaces de dimension supérieure à 2. C'est le problème de Fermat-Torricelli généralisé.
Propriétés de ce point remarquable
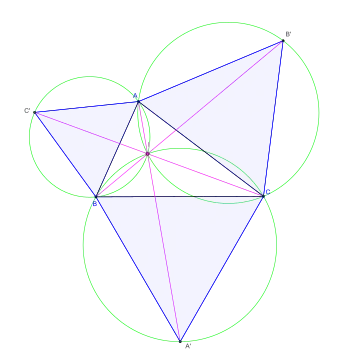
- Si ABC est bordé extérieurement par trois triangles équilatéraux , les cercles de Torricelli circonscrits à ces triangles sont concourants en un point I appelé point de Torricelli[14] (application du théorème du pivot de Forder démontré par Auguste Miquel en 1838).
- Le point I est tel que les droites (IA), (IB), (IC) forment entre elles des angles de 120°, d'où son autre appellation de premier centre isogonique du triangle (le point I "voit" les côtés du triangle sous le même angle) ; le second centre isogonique est celui construit à partir des triangles équilatéraux bordant intérieurement ABC.
- Les droites de Simpson sont concourantes en I, d'où une construction très simple.
- Si les angles du triangle sont strictement inférieurs à 120°, le point de Fermat F rendant minimale la somme FA + FB + FC est égal au point I qui est alors situé sur les segments et on a . De plus les trois longueurs sont égales à FA + FB + FC.
- Si ce n'est pas le cas, le premier centre isogonique I ne coïncide pas avec le point de Fermat F qui se trouve être un des sommets du triangle.
- Le premier centre isogonique du triangle, et donc le point de Fermat dans le cas des angles inférieurs ou égaux à 120°, est répertorié X(13) dans l'encyclopédie des centres du triangle[15]. Ses coordonnées trilinéaires sont .
- Le premier centre isogonique se trouve sur l'hyperbole de Kiepert[16].
Démonstrations
Il existe de nombreuses démonstrations pour ces propriétés, certaines utilisent des ellipses et des propriétés de distances minimales à des ellipses[17]. C'est le principe qu'utilise Evangelista Torricelli dans une de ses démonstrations[2]. On peut également travailler sur du calcul vectoriel avec produit scalaire. Il existe cependant des démonstrations utilisant des résultats simples de géométrie synthétique, principalement le théorème de l'angle inscrit et l'inégalité triangulaire. L'une utilise le théorème de Viviani et l'autre les propriétés des rotations. La figure construite est à rapprocher de la figure associée au théorème de Napoléon. On peut aussi utiliser le théorème de Jacobi, le point de Fermat étant un point de Jacobi particulier.

Construction du premier centre isogonique
- Quel que soit le triangle ABC, supposé de sens direct, les cercles circonscrits aux triangles équilatéraux extérieurs sont concourants.
En effet, Les points M du cercle circonscrit à ABC' sont définis par , et similairement pour les autres.
Donc, si I est le second point d'intersection des cercles circonscrits respectivement à ABC et ACB alors donc Le point I appartient bien alors au troisième cercle BCA'.
- Le point I est bien situé sur les trois droites . En effet
donc Le point I est bien situé sur la droite (CC') et par un raisonnement analogue sur les deux autres droites qui forment bien entre elles des angles de 120°.
Si les angles du triangle ne dépassent pas 120° le point I est intérieur au triangle et il est situé sur les segments . En effet, dans ce cas, les quadrilatères AC'BC, BA'CA et CB'AB sont convexes et leurs diagonales sont intérieures.
- Application au théorème de Napoléon.
Les droites joignant les centres des cercles (donc aussi des triangles extérieurs) sont perpendiculaires aux droites et se coupent donc en des angles de 60°. Par conséquent, les centres des cercles forment un triangle équilatéral.
Point de Fermat par le théorème de Viviani
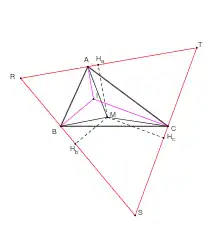
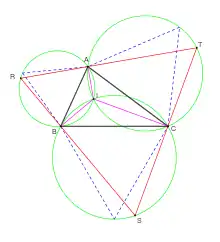
Cette démonstration s'inspire de celle publiée par Vincenzo Viviani dans son De maximis et minimis geometrica[5], Viviani publie une démonstration à attribuer à Torricelli, mais selon Vladimir Boltyanski et al.[6], la preuve sous cette forme est une version originale de Viviani.
Si A, B et C sont les projetés orthogonaux d'un même point I sur les côtés d'un triangle équilatéral RST alors ce point I est le seul point où la distance IA + IB + IC est minimale. En effet, si l'on prend un autre point M dans le plan, dont les projetés orthogonaux sur les côtés du triangle équilatéral sont Ha, Hb et Hc, la somme MA + MB + MC est strictement supérieure à la somme MHa + MHb + MHc car un des points Ha, Hb ou Hc est différent de A, B, ou C. De plus d'après le théorème de Viviani la somme MHa + MHb + MHc est égale à IA + IB + IC si M est à l'intérieur du triangle RST, elle est strictement supérieure à IA + IB + IC si M est à l'extérieur du triangle RST. Donc, dans tous les cas de figure, on a : MA + MB + MC > IA + IB + IC pour M différent de I.
Il suffit donc de prouver que A, B et C sont bien les projetés orthogonaux d'un même point I sur les côtés d'un triangle équilatéral. Les sommets de ce triangle équilatéral doivent se trouver sur les trois cercles de Torricelli. Si aucun des angles ne dépasse 120°, il suffit de prendre pour RST les points diamétralement opposés au point I intersection des trois cercles de Torricelli.
Le point d'intersection des trois cercles est alors bien l'unique point qui minimise la somme des distances aux trois sommets.
Démonstration grâce à une rotation de la minimalité au point I de la somme des distances aux sommets
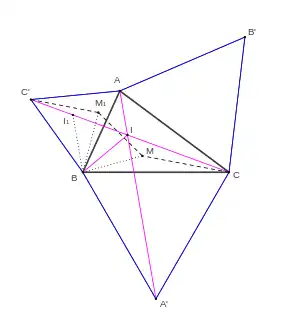
Le principe de cette démonstration est attribué tantôt à Lothar von Schrutka (1914)[18] ou son élève Bückner[19], tantôt à Tibor Gallai[18], tantôt à l'historien des mathématiques J. E. Hoffmann (1929)[20]. Elle est détaillée dans[14].
On considère la rotation de centre B et d'angle , qui envoie A en C' et A' en C. Pour tout point M du plan, on appelle M1 son image par cette rotation. La rotation étant une isométrie on a MA = M1C', et son angle étant égal à , le triangle BMM1 est équilatéral ; on a donc BM = M1M et la somme MA + MB + MC est égale à la longueur de la ligne polygonale C'M1MC.
Si les angles du triangle n'excèdent pas 120°, Le point I étant sur [AA'] son image I1 par la rotation est sur [C'C] et plus précisément sur [C'I]. La somme IA + IB + IC est égale à la longueur de la ligne polygonale C'I1IC ; les points C',I1,I,C étant alignés dans cet ordre, cette longueur est égale à C'C, et donc IA + IB + IC = C'C.
Or pour tout point M, la longueur C'M1MC est supérieure ou égale à C'C donc MA + MB + MC est supérieur ou égal à IA + IB + IC. L'inégalité est stricte si M n'est pas sur (C'C). Par un raisonnement analogue, l'inégalité est stricte si M n'est pas sur (BB') ou sur (AA'). Bref, si M est différent de I, MA + MB + MC est strictement supérieur à IA + IB + IC ce qui prouve que I est l'unique point rendant minimale la somme IA + IB + IC, et que I est bien le point de Fermat dans ce cas.
Cas d'un angle supérieur à 120°
On suppose que l'angle de sommet A mesure plus de 120° .
On étudie d'abord le cas où M est différent de A et est situé à l'intérieur (au sens large) du triangle ABC. Il existe un secteur angulaire de 120° de sommet A et s'appuyant sur AB ou AC contenant M. Sans perte de généralité, on peut supposer qu'il s'agit de BAx. La demi-droite [Ax) rencontre [MC] en C'. Le triangle ABC' a pour point de Fermat le sommet A donc MA + MB + MC' > AB + AC' de plus AC' + C'C > AC donc MA + MB + MC > AB + AC.
Il reste le cas où M est extérieur au triangle. Or, quel que soit le triangle, pour chaque point extérieur au triangle, il existe un point sur le triangle pour lequel la somme des distances soit plus petite. En effet, l'extérieur du triangle se partage en 6 zones, 2 pour chaque sommet. Soit pour le sommet A. Pour la zone 1 : le point M est dans le secteur angulaire opposé au secteur angulaire de sommet A contenant le triangle alors MB + MC > AB + AC et a fortiori MA + MB + MC > AB + AC. pour la zone 2 : le point M est intérieur au secteur angulaire de sommet A contenant le triangle mais de l'autre côté de [BC], alors le segment [AM] rencontre le segment [BC] en T et on a MB + MC > TB + TC et MA > TA donc MA + MB + MC > TA + TB + TC. Un raisonnement analogue peut se faire sur les deux autres paires de zones
Donc, si l'angle de sommet A mesure plus de 120°, pour tout point M différent de A on a MA + MB + MC > AB + AC et le point A est celui qui minimise la somme des distances.
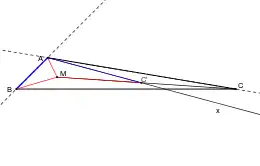 Point de Fermat - M intérieur au triangle, le secteur angulaire BAx mesure 120° |
 Point de Fermat - M extérieur au triangle - Version a - MB + MC > AB + AC |
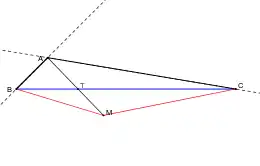 Point de Fermat - M extérieur au triangle - Version b - MB + MC > TB + TC et AM > AT |
Illustration mécanique
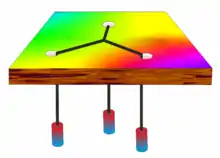
On peut illustrer ce problème de manière mécanique[21]. On dessine le triangle ABC sur une planche horizontale, et l'on perce un trou à chaque sommet. On fait passer par les trous trois ficelles à l'extrémité desquelles on suspend des poids de masse identique. On réunit ces ficelles par un nœud N. Quand le système est en équilibre, le nœud N occupe la position du point de Fermat.
Le système sera en équilibre quand l'énergie potentielle de l'ensemble sera minimale donc quand la somme des trois altitudes des trois poids sera minimale. Cela se produit quand la somme des longueurs verticales des trois ficelles est maximale, c'est-à-dire quand la somme des longueurs horizontales des trois ficelles est minimale.
Dans le cas d'un triangle dont aucun angle n'excède 120°, quand le système est en équilibre, la résultante des trois forces exercées par les poids doit être nulle. Ces trois forces peuvent être représentées par trois vecteurs de même norme d'origine N et portés par les trois ficelles. La somme des trois vecteurs est nulle seulement s'ils forment entre eux des angles de 120°.
Dans le cas où l'angle A fait plus de 120 °, le système se mettra en équilibre quand le nœud viendra se coincer en A.
Démonstration vectorielle du fait que le premier centre isogonique est bien le point de Fermat dans le cas des angles < 120°
Nous utilisons les propriétés des vecteurs et du produit scalaire dans un espace euclidien.
- Lemme 1
- Trois vecteurs unitaires (de norme 1) ont une somme nulle si et seulement si les forment deux à deux des angles de 120°.
- Preuve du Lemme 1
- Désignons par la mesure entre 0° et 180° de l'angle .
- En multipliant successivement par les , on obtient ; pour les sont donc égaux entre eux, d'où , soit .
- .Ainsi, on a bien
- Réciproquement, si les vecteurs unitaires forment deux à deux des angles de 120°, on a :
- On obtient donc
- Par conséquent :
- , c.q.f.d.
- Lemme 2
- Pour tous vecteurs et on a :
- Preuve du Lemme 2
- Pour tous vecteurs on sait que
- En prenant ,
- on obtient bien l'inégalité du Lemme 2. c.q.f.d.
Soit I l'unique point tel que d'un triangle ABC ayant des angles strictement inférieurs à 120°. Posons, pour un point M,.
D'après le lemme 1 on a : .
Or d'après le Lemme 2 :
En sommant ces trois inégalités, on obtient
- , soit
- ce qui démontre que I minimise la somme et que I est le point de Fermat.
De plus le fait que le point F minimisant la somme doit vérifier s'il est non situé sur les sommets du triangle peut se démontrer par le calcul différentiel. En effet, la différentielle de la fonction est définie, pour , par . Au minimum F cette différentielle doit être nulle donc d'où le résultat par le lemme 1[22].
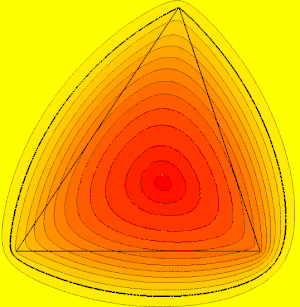
Maximisation de la somme des distances
Si l'on renomme les sommets du triangle de sorte que , le maximum de la distance aux sommets pour M décrivant la plaque triangulaire fermée ABC est atteint en A et vaut donc la somme des longueurs des deux plus grands côtés du triangle.
Ceci constitue le théorème de J.N. Visschers (1902)[23].
Références
- Pierre de Fermat et Paul Tannery, « Méthode du maximum et du minimum », dans Œuvres de Fermat (Tome III), Paris, Gauthier-Villars, (lire en ligne), p. 136 [153,154]
- E. Torricelli : Opere, vol I, Part 2, Faenza 1919, p. 90-97
- Bonaventura Cavalieri, Exercitationes geometricae sex, «De inveniendo puncto, quod a tribus datis quibusfuit distet secundum minimam quantitatem lire en ligne
- Boltyanski, Martini et Soltan 1998, p. 321
- (la) Apolonio de Pérgamo, Vincenzo Viviano, De maximis et minimis geometrica, 1659, Appendice p. 143-150
- Boltyanski, Martini et Soltan 1998, p. 314
- Thomas Simpson, The doctrine and application of fluxions, 2d ed, 1776, p. 27
- F.K. Hwang, D.S. Richards, P. Winter, The Steiner Tree Problem, Annals of Discrete Mathematics, Elsevier, 1992, p.3
- Thomas Simpson, The doctrine and application of fluxions, 2d ed, 1776, p. 28
- Thomas Simpson, The doctrine and application of fluxions, 2d ed, 1776, p. 506
- Franz Heinen, Über Systeme von Kraeften, deren Intensitaeten sich wie die n. Potenzen der Entfernungen gebenener Punkte von einem Central-Punkte verhalten: in Beziehung auf Punkte, für welche die Summe der n. Entfernungspotenzen ein Maximum oder Minimum ist, Baedeker, 1834, p=19
- (en) Hans Rademacher et Otto Toeplitz, The Enjoyment of Mathematics : Selections from Mathematics for the Amateur, Dover, , 205 p. (ISBN 978-0-486-26242-0, lire en ligne), p. 33-34. La version en allemand, (de) Von Zahlen und Figuren, Springer, (ISBN 978-3-642-62014-0, lire en ligne), p. 27 précise que L. Schruttka donna une démonstration de ce théorème dans les Mélanges de 1914 en l'honneur du 50e anniversaire du doctorat de Hermann Amandus Schwarz.
- Boltyanski, Martini et Soltan 1998, p. 318
- Yvonne et René Sortais, La géométrie du triangle, exercices résolus, Hermann, , p. 200-209
- « ENCYCLOPEDIA OF TRIANGLE CENTERS », sur faculty.evansville.edu (consulté le )
- (en) Eric W. Weisstein, « Kiepert Hyperbola », sur MathWorld.
- Point de Fermat sur le site chronomath de Serge Mehl
- Boltyanski, Martini et Soltan 1998, p. 313
- (de) Von Zahlen und Figuren, Springer, (ISBN 978-3-642-62014-0, lire en ligne), p. 27
- Nahin 2011, p. 280
- Bettinelli-Torricelli, p. 6
- Marcel Berger, Géométrie, t. 1, Cassini, , p. 236, paragraphe 9.10.6
- Eurêka, Géométriquement votre, Dunod, (lire en ligne), p. 47
Bibliographie
- Paul J. Nahin, When Least Is Best : How mathematicians discovered many clever ways to make things as small (or as large) as possible, Princeton University Press, - «The Fermat/Steiner Problem » pp=279-286
- Vladimir Boltyanski, Horst Martini et V. Valerii Petrovich Soltan, Geometric Methods and Optimization Problems, vol. 4, Springer, coll. « Combinatorial Optimization », (présentation en ligne) - § 18 : «The classical Fermat-Torricelli problem» suivi de § 23 : « Historical survey »
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4)
- Bertrand Bettinelli, « Le point de Torricelli d'un triangle » (consulté le )
- Pascal Gamblin et Daniel Perrin, « Sur le point de Fermat d’un triangle »
Lien externe
- Point de Fermat sur le site chronomath de Serge Mehl.




![{\displaystyle [AA'],[BB'],[CC']}](https://img.franco.wiki/i/2660ad280179699c998f59b7edd1894294f91032.svg)







































