Théorème de Jacobi (géométrie)

En géométrie, le théorème de Jacobi, ou théorème de Fermat-Toricelli généralisé ou théorème isogonal désigne un résultat de géométrie du triangle[1]. Un point de Jacobi est un point du plan euclidien déterminé par un triangle ABC et un triplet d'angles α, β et γ. Cette information est suffisante pour déterminer trois points X, Y et Z tels que ${\textstyle {\widehat {ZAB}}={\widehat {YAC}}=\alpha }$ , ${\textstyle {\widehat {XBC}}={\widehat {ZBA}}=\beta }$ et ${\textstyle {\widehat {YCA}}={\widehat {XCB}}=\gamma }$ . Puis, par un théorème de Karl Friedrich Andreas Jacobi (de), les droites (AX), (BY) et (CZ) sont concourantes[2] - [3] - [4] en un point N qu'on appelle point de Jacobi[4].

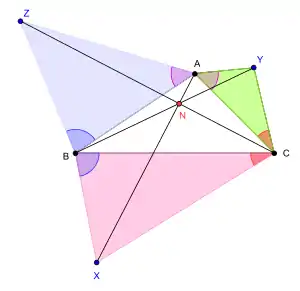
Les angles colorés adjacents sont de mesures égales. Le point N est le point de Jacobi pour le triangle ABC et ces angles.

Le point de Jacobi est une généralisation du point de Fermat, qui s'obtient en prenant α = β = γ = 60° et le triangle ABC sans angle étant supérieur ou égal à 120°.

Si les trois angles ci-dessus sont égaux, alors N se trouve sur l'hyperbole équilatère donnée en coordonnées barycentriques par

yz(\cot B-\cot C)+zx(\cot C-\cot A)+xy(\cot A-\cot B)=0,

qui est donc l'hyperbole de Kiepert. Chaque choix de trois angles égaux détermine un centre du triangle.

Applications

Les théorèmes de Lemoine, sur l'existence du point de Lemoine, et de Kariya peuvent se démontrer avec le théorème de Jacobi.

Théorème de Kariya

Dans un triangle ABC de centre de gravité I, soit XYZ son triangle de Gergonne, avec X sur [BC], Y sur [CA], Z sur [AB]. On considère, pour un nombre réel t, le triangle X_tY_tZ_t, image de XYZ par homothétie de centre I et de rapport t. Alors pour tout t, les droites (AX_t), (BY_t), (CZ_t) sont concourantes en un point P_t. De plus, quand t varie, P_t parcourt l'hyperbole de Feuerbach.

Voir aussi

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Jacobi's theorem (geometry) » (voir la liste des auteurs).

Jean-Louis AYME, « Le théorème de Jacobi - Une nouvelle approche synthétique »
(en) Michael de Villiers, Some Adventures in Euclidean Geometry, Dynamic Mathematics Learning, 2009, 138–140 p. (ISBN 9780557102952)
(en) Glenn T. Vickers, « Reciprocal Jacobi Triangles and the McCay Cubic », Forum Geometricorum, vol. 15,‎ 2015, p. 179–183 (lire en ligne)
(en) Glenn T. Vickers, « The 19 Congruent Jacobi Triangles », Forum Geometricorum, vol. 16,‎ 2016, p. 339–344 (lire en ligne)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.