Coordonnées trilinéaires

En géométrie, les coordonnées trilinéaires d'un point relativement à un triangle donné, notées $(x : y : z)$ sont, à une constante multiplicative strictement positive près, les distances algébriques relativement aux côtés (étendus) du triangle.

Les coordonnées trilinéaires d'un point intérieur sont ici données par les distances

a', b', c'

; les coordonnées trilinéaires sont alors

(ka' : kb' : kc')

pour toute constante

k

strictement positive.

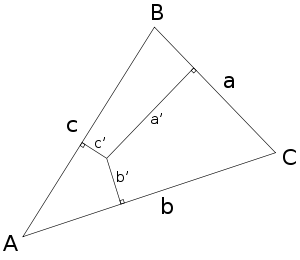
Pour un triangle $ABC$ , le rapport $x / y$ est le rapport des distances algébriques du point aux côtés $(BC)$ et $(AC)$ respectivement et ainsi de suite par permutation sur $A, B, C$ .

Le signe d'une coordonnée trilinéaire indique si le point est intérieur au triangle par rapport à un côté : par exemple, la coordonnée $x$ est positive s'il se trouve du même côté que $A$ par rapport à la droite $(BC)$ . Il est ainsi impossible que les trois coordonnées trilinéaires soient négatives.

Détermination des coordonnées trilinéaires

L'aire algébrique d'un triangle $XYZ$ est $S_{XYZ}={\frac {1}{2}}\det \left({\overrightarrow {XY}},{\overrightarrow {XZ}}\right)$ , positive si $XYZ$ est direct, négative sinon. Or $S_{XYZ}={\frac {1}{2}}YZ\times h$ où $h$ est la distance algébrique de $X$ à la droite $(YZ)$ orientée de $Y$ vers $Z$ . Pour un triangle $ABC$ de sens direct et de côtés de longueur $BC = a, AC = b, AB = c$ , les coordonnées trilinéaires d'un point $M$ sont donc :

\left({\frac {\det({\overrightarrow {MB}},{\overrightarrow {MC}})}{a}}:{\frac {\det({\overrightarrow {MC}},{\overrightarrow {MA}})}{b}}:{\frac {\det({\overrightarrow {MA}},{\overrightarrow {MB}})}{c}}\right)

\left({\frac {S_{MBC}}{a}}:{\frac {S_{MCA}}{b}}:{\frac {S_{MAB}}{c}}\right)

Le triplet $(S_{MBC},S_{MCA},S_{MAB})$ étant un triplet de coordonnées barycentriques de $M$ , on en déduit que si $M$ a pour coordonnées trilinéaires $(x : y : z)$ , il a pour coordonnées barycentriques $(ax, by, cz)$ .

Exemples

Voici les coordonnées trilinéaires de quelques points remarquables du triangle :

$A(1:0:0)$
$B(0:1:0)$
$C(0:0:1)$
milieu de $[BC]\,(0:ac:ab)$
milieu de $[CA]\,(bc:0:ba)$
milieu de $[AB]\,(cb:ca:0)$
centre du cercle inscrit $I(1:1:1)$
centre de gravité $G(bc:ca:ab){\text{ ou }}(1/a:1/b:1/c){\text{ ou }}(1/\sin {\widehat {A}}:1/\sin {\widehat {B}}:1/\sin {\widehat {C}})$
centre du cercle circonscrit $O(\cos {\widehat {A}}:\cos {\widehat {B}}:\cos {\widehat {C}})$
orthocentre $H(1/\cos {\widehat {A}}:1/\cos {\widehat {B}}:1/\cos {\widehat {C}})$
centre du cercle d'Euler $\Omega (\cos({\widehat {B}}-{\widehat {C}}):\cos({\widehat {C}}-{\widehat {A}}):\cos({\widehat {A}}-{\widehat {B}}))$
point de Lemoine $(a:b:c){\text{ ou }}(\sin {\widehat {A}}:\sin {\widehat {B}}:\sin {\widehat {C}}).$

On trouvera dans l'encyclopédie des centres de triangle (ETC) les coordonnées trilinéaires de milliers de points remarquables du triangle.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Trilinear coordinates » (voir la liste des auteurs).

Voir aussi

Liens externes

(en) Eric W. Weisstein, « Trilinear Coordinates », sur MathWorld