Compas parfait

Le compas parfait ressemble au compas « classique » : il comporte deux branches A et B faisant un angle constant β entre elles. La branche A, fixée au support, s'identifie à l'axe du cône et la branche B balaie la surface de révolution du cône autour de son axe. Le compas parfait a ainsi deux contraintes supplémentaires: la branche A reste dans un plan perpendiculaire au plan du traçage et contenant l'axe principal de la conique et forme avec cet axe un angle constant α et la branche B, décrivant la figure géométrique, est télescopique. Chacun des angles α et β a une valeur inférieure ou égale à 90° et la nature des coniques dépendra des valeurs relatives entre ces angles. Les figures se dessinent donc en faisant tourner le compas parfait autour de la branche A, soit autour de l'axe du cône, ce qui fait décrire à l'extrémité de la branche B:

• un cercle si α=90° et 0<β<90°
• une ellipse si 0<α<90° et β<α
• une portion de parabole si 0<α<90° et β=α
• une portion de demi-hyperbole si 0<α<90° et β>α
• un segment de droite si 0<α<90° et β=90°

Il est évident que si α=β=90°, le compas parfait ne pourrait pas dessiner de figure.

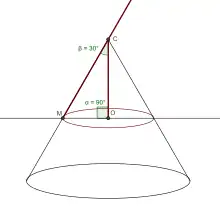Construction d'un cercle avec un compas parfait

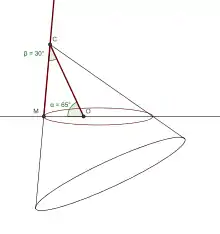Construction d'une ellipse avec un compas parfait

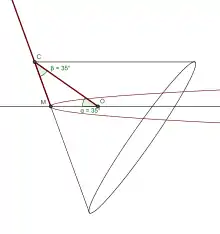Construction d'une portion de parabole avec un compas parfait

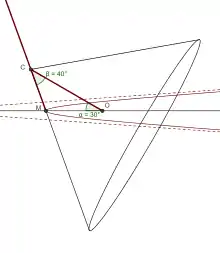Construction d'une portion de demi-hyperbole avec un compas parfait