Hexagramme de Pascal
L'hexagramme de Pascal, ou hexagramme mystique, est une figure géométrique illustrant le théorème de Pascal. Il représente un hexagone quelconque inscrit dans une conique. Ce théorème démontre que les trois intersections des côtés opposés sont alignées.

Plus précisément : dans un plan projectif satisfaisant l'axiome de Pappus (construit sur un corps commutatif), les trois intersections sont alignées, si, et seulement si, les six points sont sur une conique.
Blaise Pascal, qui aurait découvert ce théorème à seize ans (dans le plan projectif réel), lui a donné le nom d'hexagramme mystique[1].
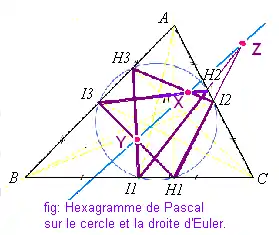
Cas particuliers
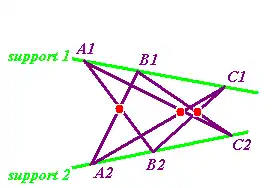
Si la conique est une bidroite, les droites forment deux supports recevant chacun trois points de l'hexagone. Il s'agit ici du théorème de Pappus.
Autres configurations
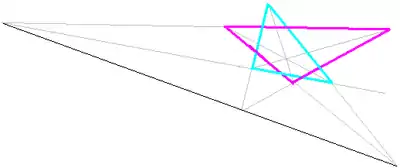
En utilisant une étoile de David irrégulière (deux triangles entrelacés), on peut retrouver les trois intersections alignées. Dans ce cas, ce n'est plus un hexagone, et l'alignement est expliqué par le théorème de Desargues.
Illustration
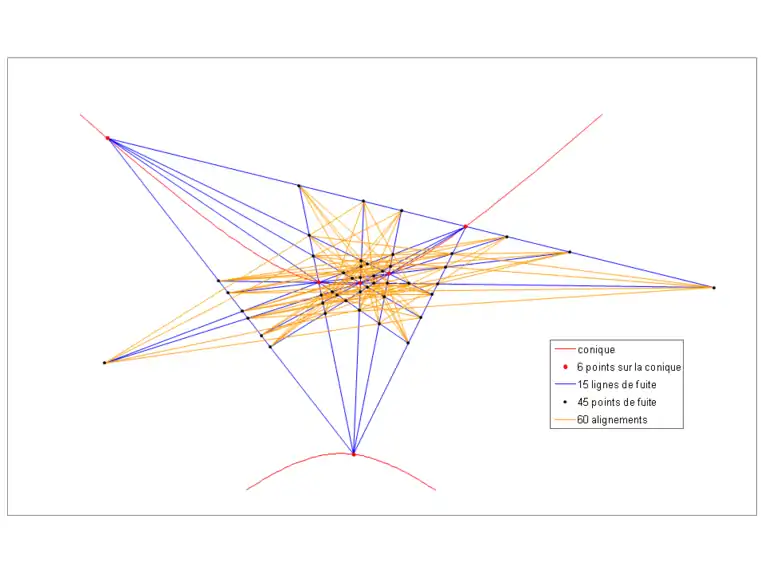
Etant donné que le théorème est valable pour un hexagone quelconque inscrit dans une conique, on obtient un alignement pour chacune des 60 permutations des sommets de l'hexagone. La figure ci-dessous montre les 60 alignements produits par ce théorème à partir de 6 points sur une hyperbole.
Notes
- Comme l'explique Leibniz dans les Notes de Leibniz et de Tschirnhaus sur les Coniques : « Hexagrammum pascallanum mysticum ut vocat idemque semper conicum. » (« Hexagramme de Pascal, mystique comme il l'appelle, et qui est toujours conique »)
Bibliographie
- Michèle Audin, Géométrie, EdP-Sciences 2005 (Geometry, Universitext, Springer), (ISBN 978-3-540-43498-6)
- Marcel Berger, Géométrie [détail des éditions] (Tome 1)
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-916352-08-4)
- De la Géométrie Projective à la Géométrie Euclidienne L'Hexagramme Mystique de Pascal
- Méthodes modernes en géométrie de Jean Fresnel
- Daniel Lehmann et Rudolf Bkouche, Initiation à la géométrie, PUF 1988, (ISBN 2 13 040160 0)
- J.-C. Sidler, Géométrie projective, InterEditions 1993