Théorème de Desargues
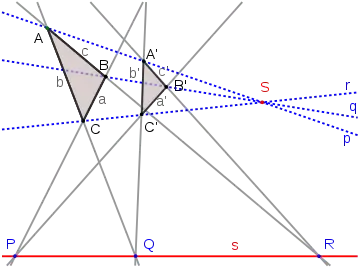
En mathématiques, le théorème de Desargues, du nom du mathématicien et architecte Girard Desargues, est un théorème de géométrie projective, qui possède plusieurs variantes en géométrie affine. Il s'énonce uniquement en matière d'alignement de points et d'intersection de droites (voir ci-contre).
Le théorème de Desargues se démontre dans un plan ou un espace construit sur un corps quelconque (non nécessairement commutatif). Il se démontre également dans un espace de dimension supérieure ou égale à 3 caractérisé axiomatiquement en matière d'incidence (par exemple, dans le cas de la géométrie affine, par les axiomes de Hilbert).
En géométrie plane il peut être pris pour axiome, et caractérise alors, parmi les plans vus comme structures d'incidence, ceux qui peuvent être construits sur un corps (voir, pour le cas affine, Plan affine (structure d'incidence) et Plan affine arguésien).
Géométrie plane
D'une forme faible du théorème de Desargues dans le plan réel, et plus généralement dans un plan sur un corps quelconque, on déduit le théorème de Desargues projectif, et, par celui-ci, la forme affine forte du théorème.
Plan affine
En géométrie affine, l'énoncé du théorème de Desargues doit être modifié et complété pour prendre en compte le parallélisme. Cependant on nomme souvent théorème de Desargues les deux cas particuliers simples qui suivent[1].
|
|
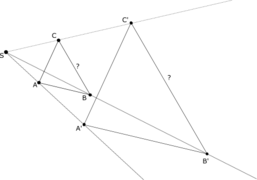
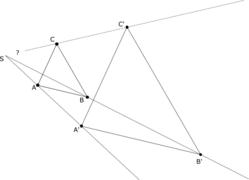
Dans la première configuration, le théorème se déduit du théorème de Thalès et de sa réciproque. Appelons S le point de concours des trois droites p, q, r. Par le théorème de Thalès dans un triangle, les rapports des mesures algébriques de SA/SA' et SB/SB' d'une part, SA/SA' et SC/SC' d'autre part sont égaux, donc SB/SB' et SC/SC' sont égaux, et par la réciproque du même théorème (BC)//(B'C').
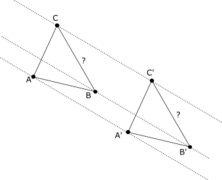
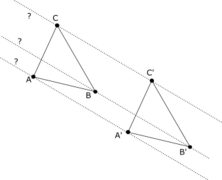
Dans la seconde configuration, on reconnaît deux parallélogrammes ayant un côté en commun ; les deux autres côtés parallèles définissent alors un parallélogramme.
La réciproque se déduit du sens direct par une méthode de « fausse position », en distinguant deux cas suivant que deux droites parmi les trois en jeu, prenons (AA') et (BB'), sont sécantes ou parallèles. Dans le premier cas soit S le point intersection de (AA') et (BB'), et M sur (SC) tel que (A'M)//(AC) : les conditions du sens direct du théorème de Desargues sont réalisées, avec, en reprenant les notations précédentes, M à la place de C', donc (MB')//(CB). Or il n'existe qu'un seul point situé, d'une part sur la parallèle à (AC) menée par A', d'autre part sur la parallèle à (BC) menée par B' et ce point est C'. Donc M et C' sont confondus et les points SCC' sont alignés. Le second cas se déduit également du sens direct de façon analogue.
La démonstration qui précède ne suppose nullement que le plan est euclidien, ni même que les scalaires sont les réels, puisqu'elle n'utilise que le théorème de Thalès dans un plan affine sur un corps quelconque (la notion de rapport de deux mesures algébriques sur une droite est purement affine, voir l'article lié).
Une autre démonstration — toujours pour un plan affine sur un corps quelconque — consiste à remarquer que les deux configurations du théorème de Desargues affine font apparaître l'une une homothétie, l'autre une translation, et à utiliser les propriétés de ces transformations affines, qui transforment une droite en une droite parallèle[2].
Plan projectif
L'énoncé donné au début de l'article se décompose en deux implications, dont l'une est duale de l'autre. En effet, nommons les droites qui sont les côtés des deux triangles ABC et A'B'C' de la façon suivante : a = (BC), a' = (B'C'), b = (AC), b' = (A'C'), c = (AB), c' = (A'B'). Le théorème de Desargues peut s'énoncer comme suit.
Théorème de Desargues projectif — Les deux triangles (non plats) ABC et A'B'C' de côtés a, b, c et a', b', c' nommés comme indiqué en préambule, ont leurs sommets deux à deux distincts, A de A', B de B' et C de C', sur trois droites distinctes p = (AA') , q = (BB') et r = (CC') :
- si les trois droites p, q et r sont concourantes en un même point, alors les trois points P = a ∩ a', Q = b ∩ b' et R = c ∩ c' sont alignés ;
- si les trois points P, Q et R sont alignés, alors les trois droites p, q et r sont concourantes en un même point.
Le sens direct du théorème de Desargues projectif se réduit au sens direct du théorème de Desargues affine (forme faible ci-dessus), de la façon suivante[3]. On choisit deux des points, par exemple Q et R, et la droite (QR) comme droite à l'infini. Le complémentaire de cette droite dans le plan projectif a alors une structure de plan affine. Dans ce plan affine, R est à l'infini se traduit par (AB)//(A'B'), et Q à l'infini par (AC)//(A'C'). L'hypothèse de concours en S des droites p, q, et r se traduit par p, q et r sont concourantes ou parallèles, suivant que le point de concours S est sur la droite à l'infini (QR) ou non. Ces deux cas sont exactement les deux cas de la forme affine faible ci-dessus, dont les hypothèses sont alors vérifiées, et on conclut dans chacun des deux cas que (BC)//(B'C'). Mais interprété dans le plan projectif, ceci signifie que p = (BC) ∩ (B'C') est à l'infini, c'est-à-dire sur la droite (QR) et le théorème de Desargues projectif (sens direct) est démontré.
La réciproque se déduit par dualité (on pourrait aussi la déduire de la réciproque du théorème affine faible, mais aussi, a contrario, déduire la réciproque du théorème affine par dualité, via le plan projectif).
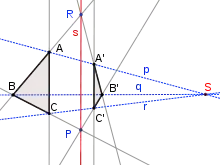
Retour au plan affine
On déduit du théorème de Desargues projectif la forme affine forte, qui s'énonce moins aisément, le théorème étant essentiellement projectif[4]. On l'obtient en choisissant comme droite à l'infini une droite quelconque du plan projectif. À chaque point à l'infini correspond en affine une direction de droites (toutes les droites parallèles à une droite donnée). Trois droites concourantes en projectifs peuvent être, soit parallèles, soit sécantes, dans le plan affine obtenu, suivant que le point de concours est ou non à l'infini. Trois points alignés correspondent, soit à trois points alignés (aucun d'entre eux n'est à l'infini), soit à trois directions de droites parallèles (tous les trois sont à l'infini), soit à deux points et une direction de droite parallèle à la droite passant par ces deux points (un seul des trois points à l'infini).
L'énoncé du théorème est alors le suivant :
Théorème de Desargues affine (forme forte) — Les deux triangles (non plats) ABC et A'B'C' ont leurs sommets deux à deux distincts, A de A', B de B' et C de C', sur trois droites distinctes p = (AA') , q = (BB') et r = (CC'). Alors les trois droites (AA'), (BB') et (CC') sont parallèles ou concourantes si et seulement si l'une des trois conditions suivantes est réalisée :
- les droites (BC) et (B'C') sont sécantes, de même (AC) et (A'C'), de même (AB) et (A'B'), et les points P = (BC)∩(B'C'), Q = (AC)∩ (A'C') et R = (AB)∩(A'B') sont alignés ;
- deux parmi les trois couples de droites (BC) et (B'C'), (AC) et (A'C'), (AB) et (A'B') sont des couples de droites sécantes et le dernier couple formé de deux droites parallèles de direction la droite passant par les deux premiers points d'intersection, par exemple P = (BC)∩(B'C'), Q = (AC)∩(A'C') et les droites (AB) et (A'') sont parallèles entre elles et à la droite (PQ) ;
- les trois couples de droites précités sont des couples de droites parallèles : (BC) // (B'C'), (AC) // (A'C'), (AB) // (A'B').
Définition axiomatique
Dans son livre Grundlagen der Geometrie (Les fondements de la géométrie) publié en 1899, David Hilbert axiomatise la géométrie euclidienne (en dimension 2 ou 3), en identifiant plusieurs groupes d'axiomes qui fournissent une spécialisation progressive vers la géométrie euclidienne. Ses axiomes utilisent 3 sortes d'objets, les points, les droites et les plans, et des relations entre ces objets, dites depuis d'incidence (un point est sur la droite ou la droite passe par ce point). Dans le cas du plan, le premier groupe d'axiomes équivaut au suivant (voir plan affine (structure d'incidence)) :
- par deux points distincts passe une et une seule droite ;
- toute droite passe par au moins deux points. Il existe au moins trois points non alignés ;
- par un point A extérieur à une droite d, il ne passe qu'une seule droite parallèle à d (c'est-à-dire qu'il n'y a pas de point sur cette droite et sur d).
Le théorème de Desargues s'énonce en matière d'incidence, mais Hilbert met en évidence que ces axiomes ne permettent pas de le démontrer. Il faut soit considérer que ce plan est plongé dans l'espace (voir infra), et les axiomes d'incidence de la géométrie dans l'espace sont alors suffisants, soit utiliser les axiomes de congruence[5] (qui permettent d'introduire la longueur des segments, et la mesure des angles).
En d'autres termes, cet énoncé a valeur d'axiome en géométrie affine plane, de même qu'en géométrie projective plane (où tout ceci se transpose directement). Il suffit de prendre pour axiome le sens direct, puisque la réciproque se déduit de celui-ci par les axiomes d'incidence (voir ci-dessus la démonstration dans le cas affine[6]).
Les plans, affines ou projectifs, pour lesquels il est valable sont appelés plans arguésiens (ou désarguésiens)[7] et sont les mêmes que les plans, affine ou projectif, construits sur un corps quelconque (non nécessairement commutatif). Il existe également des plans non arguésiens, satisfaisant les axiomes d'incidence ci-dessus, mais où le théorème de Desargues n'est pas valide, comme celui découvert par Hilbert[5], ou celui plus simple découvert par Moulton en 1902.
Il est possible également de déduire le théorème de Desargues d'un axiome plus fort. Ainsi, le théorème de Hessenberg[8] déduit le théorème de Desargues du « théorème » de Pappus, pris alors comme axiome. L'axiome de Pappus caractérise (en plus des axiomes d'incidence) les plans sur un corps commutatif[8].
Espace
Le théorème de Desargues se généralise dans un espace de dimension supérieure, aussi bien en affine qu'en projectif. L'énoncé est à chaque fois essentiellement le même qu'en géométrie plane, mais les triangles ne sont pas nécessairement coplanaires.
Le théorème de Desargues se démontre, pour des triangles coplanaires ou non, dans un espace de dimension quelconque sur un corps (non nécessairement commutatif), mais également dans un espace de dimension supérieure ou égale à 3, avec dans le cas affine, les seuls axiomes d'incidence (parmi par exemple les axiomes de Hilbert), et de même en projectif. La géométrie non arguesienne n'existe qu'en dimension 2.
Géométrie projective
Les axiomes très simples suivants, dus à Veblen et Young (en)[9], caractérisent les espaces projectifs de dimension quelconque, à partir de la dimension 2, le plan pouvant être non arguésien en dimension 2[10]. On suppose donnés un ensemble non vide de points E, un ensemble de droites L, et une relation d'incidence.
- Par deux points distincts passe une droite et une seule.
- Si A,B,C,D sont 4 points distincts de E tels que les droites (AB) et (CD) soient sécantes, alors les droites (AC) et (BD) sont sécantes.
- Toute droite passe par au moins 3 points.
Un sous-espace de E est un ensemble de points F tel que si deux points distincts d'une droite appartiennent à F alors tous les points de cette droite appartiennent à F. On peut donc définir le sous-espace engendré par un ensemble de points, qui est le plus petit sous-espace contenant ceux-ci. Un espace projectif, ou un sous-espace projectif est de dimension finie n s'il est engendré par n + 1 points et n'est pas engendré par n points. Un sous-espace engendré par 3 points non alignés est un plan projectif, et on montre que deux droites distinctes d'un plan projectif sont toujours sécantes en un point, grâce au second axiome des espaces projectifs[11].
Le théorème de Desargues ne se démontre que si l'on suppose que l'espace est au moins de dimension 3, c'est-à-dire que l'on ajoute l'axiome :
- il existe 3 points non alignés, et un point n'appartenant pas au plan engendré par les points précédents.
Cet axiome revient à l'existence de deux droites non sécantes. On axiomatise le plan projectif en ajoutant l'axiome contraire que deux droites sont toujours sécantes (le second axiome est alors inutile), et un axiome pour avoir « suffisamment » de points, mais ces axiomes ne permettent pas de démontrer le théorème de Desargues.
L'énoncé du théorème est à peine modifié, le fait que les points d'intersection, nommés ci-dessus P, Q et R existent bien est maintenant une conséquence de l'hypothèse dans le cas où les triangles ne sont pas coplanaires. La démonstration du sens direct est détaillée ci-dessous :
Les deux triangles (non plats) ABC et A'B'C' ont leurs sommets 2 à deux distincts, A de A', B de B' et C de C', sur 3 droites distinctes p = (AA') , q = (BB') et r = (CC'). Si les 3 droites p = (AA'), q = (BB') et r = (CC') sont concourantes (en un point S) alors les 2 droites (BC) et (B'C') sont sécantes, de même (AC) et (A'C'), de même (AB) et (A'B') et les 3 points d'intersection obtenus P = (BC)∩(B'C'), Q = (AC)∩(A'C') et R = (AB)∩(A'B') sont alignés.
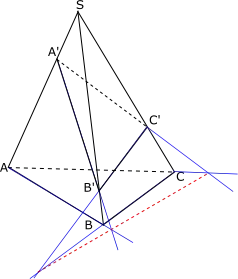
La démonstration qui suit est alors très voisine de celle mise en place par Desargues en 1638[12].
Cas de triangles non coplanaires
Les hypothèses sont celles du théorème de Desargues. Supposons ABC et A'B'C' non coplanaires, et les droites (AA'), (BB') et (CC') sécantes en un point S. Alors les droites (AA') et (BB') sont sécantes, donc coplanaires, et les droites (AB) et (A'B') sont donc sécantes en un point R (second axiome des espaces projectifs). L'hypothèse donne de même que les droites (AC) et (A'C') sont sécantes en un point Q, et (BC) et (B'C') sécantes en un point R. Alors les plans (ABC) et (A’B’C’) sont distincts et contiennent tous deux P, Q et R. Leur intersection est donc une droite qui contient ces trois points et P, Q et R sont alignés.
Cas de triangles coplanaires
Toujours dans un espace de dimension supérieure ou égale à 3, on suppose que les deux triangles sont dans un même plan ∏. On remarque que le dessin donné en introduction, peut être vu comme une représentation en perspective d'un dessin en dimension 3, c'est-à-dire que l'on peut considérer ces triangles comme des projetés sur un plan de triangles non coplanaires. La démonstration est détaillée plus formellement ci-dessous.
On choisit alors un point O extérieur à ∏, et un point M sur la droite (OC). Les points S, M et M' étant alignés dans ∏, les points 0, S, M, M' sont dans un même plan et (SM) et (OC') sont sécantes, on définit alors M’=(SM)∩(0C’). Les triangles ABM et A’B’M’ sont alors dans la configuration précédente et les points d’intersection R, Q0= (AM)∩(A'M') et P0 = (BM)∩(B'M') sont alignés. Par projection centrale de sommet O sur ∏, on a :
- A→A, B→B, A’→A’, B’→B’ (points de ∏)
- M→C, M’→C’ (par définition)
d’où :
- (AB)→(AB), (A’B’)→(A’B’), (AM)→(AC), (A’M’)→(A’C’), (BM)→(BC), (B’M’)→(B’C’)
et donc
- R→R, Q0→Q et P0→P.
L'alignement de R, Q0 et P0 entraîne alors celui de R, Q et P. On a introduit une projection conique, mais il est facile d'observer que la démonstration n'utilise réellement que les propriétés d'alignement et d'intersection données par les axiomes.
Notes et références
- Yves Ladegaillerie, Géométrie affine, projective, euclidienne et anallagmatique, Ellipses, , 515 p. (ISBN 978-2-7298-1416-8), p. 35 et 85 ; ceux-ci sont en effet suffisants pour en déduire le cas général en projectif (Ladegaillerie 2003, p. 113).
- Par exemple Jean Fresnel, Méthodes modernes en géométrie, Hermann, , 408 p. (ISBN 2-7056-1437-0), p. 45.
- Par exemple Fresnel 1996, p. 69.
- Ladegaillerie 2003, p. 113.
- Yves Martin, « Géométrie non arguésienne dynamique », sur math.ens.fr/culturemath (ressources pour les enseignants de mathématiques, site expert des Écoles normales supérieures et du ministère de l'Éducation nationale), IREM de La Réunion, , 1. Desargues et Hilbert.
- Jacqueline Lelong-Ferrand, Fondements de la géométrie, PUF, , 287 p. (ISBN 978-2-13-038851-7), p. 179 dans le cas des droites concourantes ; il suffit d'énoncer l'axiome pour 3 droites concourantes, car le cas des droites parallèles se déduit de celui-ci via cette réciproque, Lelong-Ferrand même page.
- Lelong-Ferrand 1985, p. 178. L'appellation « plan arguésien » remonte à Hilbert selon Martin 2007.
- Lelong-Ferrand 1985, p. 187.
- Lelong-Ferrand 1985, p. 197.
- Ils ont en géométrie affine leurs équivalents qui, également, permettent de caractériser tous les espaces affines de dimension quelconque (Lelong-Ferrand 1985, p. 202) et ne sont pas restreints à la dimension 2 ou 3 comme ceux de Hilbert.
- Lelong-Ferrand 1985, p. 198.
- Œuvres de Desargues, Première proposition géométrique, aperçu sur Google Livres, extrait de la perspective de Bosse (1648).
Voir aussi
Articles connexes
- Théorème de Monge (géométrie élémentaire)
- Plan projectif (structure d'incidence) des plans projectifs qui ne satisfont pas nécessairement la propriété de Desargues
- Plan projectif arguésien
Lien externe
(en) M. I. Voitsekhovskii, « Desargues assumption », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
Bibliographie
- (en) H. S. M. Coxeter, Introduction to Geometry [détail des éditions]
- (en) David Hilbert et Stephan Cohn-Vossen, Geometry and the Imagination [détail des éditions], p. 119-128