Plan projectif arguésien

Dans une approche axiomatique de la géométrie projective, un plan projectif est une structure comprenant un ensemble de points, un ensemble de droites, et une relation, dite d'incidence, entre points et droites (un point est sur une droite) qui vérifie les axiomes d'incidence. S'il satisfait de plus le théorème de Desargues, pris alors comme axiome, il s'agit d'un plan projectif arguésien (ou desarguésien, ou encore plan projectif de Desargues).

Le plan projectif réel « usuel » est arguésien, et plus généralement un plan projectif P²(K) définis sur un corps quelconque K (non nécessairement commutatif) est arguésien. Réciproquement, étant donné un plan projectif arguésien, il est possible de construire un corps K de façon que ce plan soit isomorphe (pour la structure d'incidence) à P²(K). Il s'agit donc d'une approche axiomatique en termes d'incidence, de la notion de plan projectif sur un corps quelconque, et une fois que le corps est caractérisé, il est possible par exemple d'introduire les coordonnées homogènes.

Si le plan vérifie de plus l'axiome de Pappus, c'est un plan projectif de Pappus et cet axiome équivaut à la commutativité du corps sous-jacent.

On retrouve exactement les mêmes correspondances en géométrie affine, un plan projectif arguésien auquel on ôte une droite, dite alors droite à l'infini, et les points qui lui sont incidents, dits alors points à l'infini, a une structure de plan affine arguésien, de même pour le plan projectif de Pappus, et c'est d'ailleurs une façon de retrouver le corps, par les rapports d'homothétie (notion affine).

À partir de la dimension 3, la propriété de Desargues (dans le plan) se démontre par les seuls axiomes d'incidence, et les espaces projectifs axiomatisés en termes d'incidence sont tous des espaces projectifs sur un corps. Tout plan affine arguésien se plonge dans un espace projectif de dimension 3 (ou supérieure) et réciproquement un tel plan est nécessairement arguésien.

Axiome de Desargues : les deux triangles (non plats) ABC et A'B'C' ont leurs sommets sur 3 droites distinctes p = (AA'), q = (BB') et r = (CC') ; si ces 3 droites sont concourantes (en S) alors les points P = (BC) ∩ (B'C'), Q = (AC) ∩ (A'C') et R = (AB) ∩ (A'B') sont alignés (sur la droite s).

Plan projectif arguésien

Axiomes

Un plan projectif arguésien vérifie, en plus des axiomes d'incidence du plan projectif, l’axiome de Desargues, soit au total :

Pour deux points distincts il existe une et une seule droite qui leur est incidente.
Deux droites distinctes ont un et un seul point commun.
Chaque droite passe par au moins 3 points.
Il existe trois points non alignés.
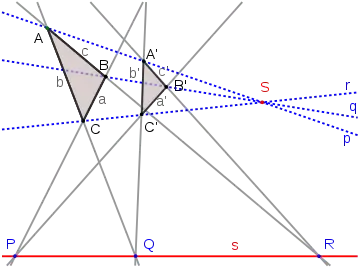
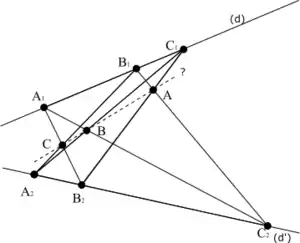
Axiome de Desargues : Étant donnés deux triangles ABC et A'B'C', si les 3 droites p = (AA'), q = (BB') et r = (CC') sont concourantes alors les 3 points d'intersection P = (BC) ∩ (B'C'), Q = (AC) ∩ (A'C') et R = (AB) ∩ (A'B') sont alignés.

L'énoncé dual de l'axiome de Desargues dit qu'étant donné deux triangles de côtés a, b, c et a', b', c', de sommets respectivement A = b ∩ c, B = a ∩ c, C = a ∩ b et A' = b' ∩ c', B' = a' ∩ c', C' = a' ∩ b', si les 3 points P = a ∩ a', Q = b ∩ b' et R = c ∩ c' sont alignés alors les 3 droites p = (AA'), q = (BB') et r = (CC') sont concourantes : c'est la réciproque de l'axiome de Desargues. Celle-ci de déduit de l'axiome. En effet supposons P, Q et R alignés, les deux triangles AA'Q et BB'P ont leurs sommets sur 3 droites (AB), (A'B') et (QP) concourantes en R. Par l'axiome de Desargues les 3 points C = (AQ) ∩ (BP), C' = (A'Q) ∩ (B'P) et (AA') ∩ (BB') sont alignés ce qui signifie bien que les 3 droites (AA'), (BB') et (CC') sont concourantes.

L'énoncé dual de l'axiome de Desargues étant démontrable, le principe de dualité, déjà valide pour les 4 premiers axiomes (voir plan projectif (structure d'incidence)#Dualité) est encore valide pour les plans projectifs arguésiens. Dit d'une autre façon, le plan dual d'un plan projectif arguésien est un plan projectif arguésien.

Plan projectif et plan affine

Un plan projectif privé d'une de ses droites, appelée alors droite à l'infini, et des points incidents à celle-ci, appelés alors points à l'infini, est un plan affine ; les droites sécantes en un point à l'infini sont parallèles (voir plan projectif (structure d'incidence)#Plan projectif et plan affine). Si le plan projectif est arguésien, quel que soit le choix de la droite le plan affine obtenu est un plan affine arguésien, l'axiome de Desargues affine correspond au cas particulier de l'axiome projectif où 2 des 3 points d'intersection sont à l'infini (la conclusion étant que le troisième l'est).

Réciproquement un plan affine arguésien peut être complété en un plan projectif, en ajoutant un point pour chaque direction de droite et une droite auxquels tous ces points et seulement ceux-ci sont incidents. Mais comme un plan affine arguésien est un plan défini sur un corps (voir paragraphe suivant), le plan projectif obtenu est le complété projectif de ce plan affine, et c'est donc un plan projectif défini sur un corps, donc arguésien (voir paragraphe suivant).

Corps sous-jacent

L'axiome de Desargues projectif est vérifié par les plans définis sur un corps (non nécessairement commutatif), c'est le théorème de Desargues.

Un plan affine arguésien étant un plan affine défini sur un corps, un plan projectif arguésien est un plan projectif défini sur un corps. La définition axiomatique des plans projectifs arguésiens s'avère donc équivalente à la définition des plans projectifs comme quotient par la relation d'alignement sur un espace vectoriel sur le corps K de dimension 3.

On peut montrer ce résultat en géométrie affine en utilisant les transformations du plan qui à une droite associent une droite parallèle. Parmi ces transformations affines, celles qui n'ont pas de point fixe sont les translations, et ceci utilise le petit axiome de Desargues affine, qui correspond, en géométrie projective, au cas particulier de l'axiome de Desargues où le point S du dessin ci-dessus est sur la droite passant par deux des points d'intersection, par exemple P et Q (prise comme droite à l'infini), la conclusion étant alors que le troisième R est sur cette droite. Les transformations qui à une droite associent une droite parallèle et qui possèdent un point fixe sont les homothéties, et ceci utilise l'axiome de Desargues, correspondant en projectif au cas où le point S n'est pas sur une droite passant par 2 des 3 points P, Q et R. Les translations fournissent l'espace vectoriel sous-jacent, sur lequel on définit, par les homothéties affines, les homothéties vectorielles qui fournissent le corps K sous-jacent.

Pour obtenir un plan projectif sur un corps, on peut donc restreindre l'axiome de Desargues au cas où deux des points d'intersection, par exemple P et Q, sont sur une droite donnée. On peut même supposer que S n'est pas aligné avec P et Q, le petit axiome de Desargues affine étant conséquence du cas correspondant aux homothéties[1]. Le plan projectif obtenu est arguésien.

Par contre le petit axiome de Desargues projectif (cas particulier où par hypothèse le point S est aligné avec deux des 3 points d'intersection, par exemple P et Q) n'est pas suffisant pour que le plan soit arguésien.

Il est également possible de mettre en évidence le corps sous-jacent directement en géométrie projective, sans détour par la géométrie affine, en utilisant une méthode inspirée de l'« algèbre des jets » de Karl Georg Christian von Staudt, mais clarifiée et simplifiée depuis[2].

Axiome de Pappus : si les points A₁, B₁ et C₁ sont alignés, de même que les points A₂, B₂ et C₂, le tout sur deux droites distinctes, alors les points A₀ =(B₁C₂) ∩ (C₁B₂), B₀ =(A₁C₂) ∩ (C₁A₂), et C₀ = (A₁B₂) ∩ (B₁C₂) sont aussi alignés. Son énoncé dual : si les droites a₁, b₁ et c₁ sont concourantes, de même que les droites a₂, b₂ et c₂, le tout en deux points distincts, alors les droites a₀ passant par b₁ ∩ c₂ et c₁ ∩ b₂, b₀ passant par a₁ ∩ c₂ et c₁ ∩ a₂, et c₀ passant par a₁ ∩ b₂ et b₁ ∩ c₂ sont aussi concourantes.

Plan projectif de Pappus

Un plan projectif de Pappus est un plan projectif arguésien qui vérifie de plus l’axiome de Pappus :

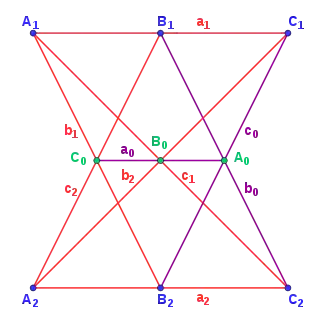
Axiome de Pappus-projectif : si les points A₁, B₁ et C₁ sont alignés sur a₁, et les points A₂, B₂ et C₂ sur a₂, ces deux droites a₁ et a₂ étant distinctes, alors les points (B₁C₂) ∩ (C₁B₂), (A₁C₂) ∩ (C₁A₂), et (A₁B₂) ∩ (B₁C₂) sont aussi alignés.

La configuration de Pappus, constituée de 9 points chacun sur 3 droites, et de 9 droites chacune passant par 3 points, est autoduale, et l'énoncé dual de l'axiome de Pappus (énoncé ci-contre) est conséquence de ce dernier modulo les axiomes d'incidence[3].

En effet, soient a₁, b₁ et c₁ 3 droites concourantes; de même que les droites a₂, b₂ et c₂. On peut donc définir 3 points A₁= a₁ ∩ b₁ ∩ c₁, B₁ = a₁ ∩ c₂ et C₁ = a₁ ∩ b₂ alignés sur a₁, ainsi que 3 points A₂ = a₂ ∩ b₂ ∩ c₂, B₂ = a₂ ∩ c₁ et C₂ = a₂ ∩ b₁ alignés sur a₂. On pose ensuite C₀ = b₁ ∩ c₂, B₀ = b₂ ∩ c₁, a₀ = (B₀C₀), b₀ = (B₁C₂), c₀ = (C₁B₂), A₀ = b₀ ∩ c₀. L'axiome de Pappus entraîne alors que les points A₀, B₀, et C₀ sont alignés, d'où la conclusion cherchée à savoir que les droites a₀, b₀, et c₀ sont concourantes.

Le principe de dualité s'étend donc aux plans projectifs de Pappus[3].

L'énoncé dual de l'axiome de Pappus est en fait équivalent à celui-ci modulo les axiomes d'incidence. La réciproque suit en effet par dualité (pour les seuls axiomes d'incidence).

Dans un plan projectif arguésien, donc qui peut se construire sur un corps, l'axiome de Pappus équivaut à la commutativité du corps en question. Il existe des corps non commutatifs, donc des plans projectifs arguésiens qui ne sont pas des plans de Pappus.

L'équivalence peut se démontrer en passant par la géométrie affine, l'axiome de Pappus affine est obtenu en faisant passer la droite à l'infini par deux des points d'intersection, la conclusion étant que le troisième l'est également. Dans le cas où les droites passant par A₁, B₁ et C₁ d'une part, A₂, B₂ et C₂ d'autre part, sont sécantes en un point O, l'axiome de Pappus affine exprime la commutativité du produit de deux homothéties de centre 0, et donc celle du corps[4].

Il est également possible de démontrer directement le résultat en géométrie projective, en utilisant les coordonnées homogènes dans un corps (a priori quelconque), puisqu'on suppose le plan arguésien, et en choisissant un repère projectif parmi les 9 points de la configuration de Pappus[5].

Il s'avère qu'en fait, comme l'a remarqué Gerhard Hessenberg, la propriété de Desargues se déduit de celle de Pappus, et donc un plan projectif de Pappus est axiomatisé par les axiomes d'incidence de plan projectif plus l'axiome de Pappus (l'axiome de Desargues est redondant).

Une autre axiomatisation des plans projectifs de Pappus (donc sur un corps commutatif) est possible, qui utilise les homographies, c'est-à-dire les transformations projectives, entre droites du plan : un axiome supplémentaire assure l'unicité d'une homographie d'une droite sur elle-même ayant 3 points fixes[6]. Elle permet de développer une approche axiomatique directe de la géométrie projective (sans utiliser l'algèbre linéaire ou les coordonnées homogènes) jusqu'à une définition et l'étude des coniques[7]

Transformations projectives entre droites du plan

Dans l'approche axiomatique on distingue le plus souvent une droite et l'ensemble des points de cette droite (c'est-à-dire incidents à celle-ci). L'ensemble des points d'une droite est un sous-espace projectif de dimension 1 (au sens de l'algèbre linéaire) dans un plan projectif arguésien. La notion duale est celle de faisceau de droites passant par un point donné, ou pinceau de droites passant par ce point ((en)pencil). C'est l'ensemble de toutes les droites passant par ce point, et les pinceaux de droites sont les sous-espaces de dimension 1 du plan projectif dual. Les transformations projectives, ou homographies, ou parfois projectivités ((en)projectivities) entre droites peuvent être définies par l'algèbre linéaire : par passage au quotient à partir des applications linéaires d'un espace vectoriel de dimension 3. Mais, dans le cadre axiomatique, elles peuvent être introduites directement, comme composées de transformations projectives particulières, qui sont les perspectives, ou projections centrales, d'une droite sur une autre.

Transformations et configurations utiles

Harmonie dans un plan projectif arguésien

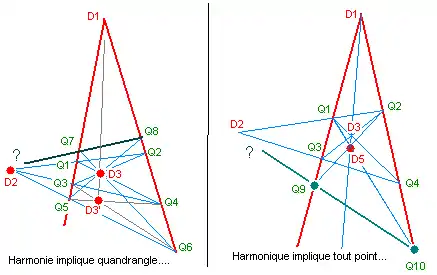Concernant les quadruplets harmoniques, l'axiome de Désargues permet de prouver au moins deux théorèmes.

Si un quadruplet est harmonique, alors il existe au moins un autre quadrangle complet qui correspond à ce quadruplet. (figure de gauche)- Soit le quadrangle Q1 Q2 Q3 Q4 qui sert à définir le quadruplet harmonique {Q1Q3, Q2Q4, D2, D3}. Nous pouvons construire un autre quadrangle complet ayant la même propriété en traçant la droite arbitraire Q5Q6 qui passe par D2 puis l'intersection D3' des droites Q3Q6 et Q4Q5, puis les intersections Q7 et Q8. La démonstration emploie deux fois de suite l'axiome de Désargues. Dans les triangles D3Q1Q2 et D3'Q5Q6 les intersections D2, Q3, Q4 sont alignées, donc d'après le dual de Désargues les rayons D3D3', Q1Q5 et Q2Q6 sont concourants, donc D1 D3 D3' sont alignés. Ensuite, les triangles Q3Q4D3' et Q7Q8D3 sont en situation perspective arguésienne, par conséquent les côtés homologues ont leurs intersections alignées : Q5Q6 et Q7Q8 se coupent en D2. Par conséquent le quadrangle Q5Q6Q7Q8 a 2 points diagonaux D2 et D3 qui sont harmoniques avec 2 côtés Q1Q3 et Q2Q4, ce qui est bien le quadruplet du début.

Le deuxième théorème, figure de droite, s'énonce ainsi : Soit un quadruplet harmonique {Q1Q3, Q2Q4, D2, D3} et D5 un point quelconque sauf D1 de la droite D3D1. Alors le quadruplet {Q1Q3, Q2Q4, D2, D3} est lui aussi harmonique. La démonstration se fait en appliquant l'axiome de Désargues aux triangles Q3Q4D3 et Q9Q10D5. Ce théorème est très utile, il exprime que dans un quadruplet harmonique on peut faire coulisser chacun des points sur la droite qui le joint au sommet de la bidroite.

Lien entre les figures de Ceva et de Menelaus dans un plan projectif arguésien

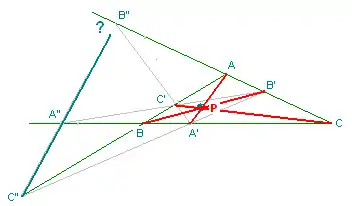
Soit un triangle ABC, un point P non situé sur un côté du triangle ; les droites AP, BP, CP s'appellent céviennes du point P, les intersections A' B' C' s'appellent les pieds des céviennes de P, du nom de Giovanni Ceva (1647-1734) ; le quadrangle complet C' B' B C permet de mettre en évidence le conjugué harmonique A", idem pour B" et C". Or les triangles ABC et A'B'C' sont en perspective arguésienne, donc les points A"B"C" sont alignés sur une droite que l'on appelle ménélienne, du nom de Ménélaos d'Alexandrie (I^er siècle). D'où le théorème à la formulation moins élégante que la figure : Dans un triangle, les points conjugués harmoniques des pieds des céviennes, points situés sur les côtés du triangle, sont alignés sur une ménélienne.

Configurations unidimensionnelles

Les 2 configurations unidimensionnelles élémentaires du plan projectif d'incidence (PPI) sont : la droite, ensemble de points alignés ainsi que le « faisceau », ensemble de droites concourantes en un point.

On pourra ensuite étudier le « faisceau de coniques », ensemble de coniques qui ont 4 points communs, etc.

Transformations de configurations unidimensionnelles

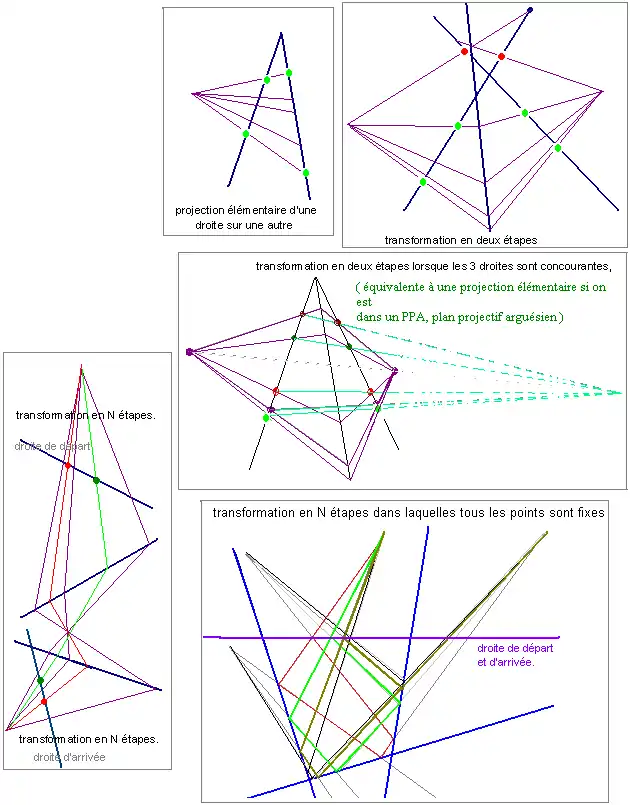
Dans le droit héritage de la perspective de la Renaissance il est intéressant d'étudier certaines transformations telles que les transformations d'un alignement de points en un autre alignement de points, que l'on appelle les transformations unidimensionnelles. Par exemple la projection élémentaire d'une droite sur une autre, la transformation en deux étapes, la transformation en deux étapes lorsque les 3 droites sont concourantes, la transformation en N étapes. Quels sont les invariants d'une telle transformation, quels axiomes sont indispensables ?

Transformation projective unidimensionnelle identité sur une droite

Lorsque l'on effectue une transformation unidimensionnelle en N étapes et que l'on revient sur la droite de départ, quelles sont les conditions pour que cette transformation laisse tous les points fixes ?

Transformations projectives bidimensionnelles

Sur un plan en dimension 2, on envisage aussi les transformations bidimensionnelles, celles qui transforment un point du plan en un autre point du plan. Parmi elles, celles qui conservent l'alignement des points ; conservent-elles aussi la convergence des droites ? Parmi elles, celles qui laissent fixes seulement les points d'une droite particulière, appelées dilatations. Comment ces différentes transformations se combinent-elles, leur loi de composition interne fait-elle apparaître des structures de monoïde, de groupe, le produit de 2 transformations est-il toujours commutatif ?

Quelques configurations utiles.

Un bipoint projectif n'a rien à voir avec les vecteurs classiques, c'est simplement un ensemble non ordonné de 2 points. Idem pour la bidroite.
Un triangle est un ensemble non ordonné de 3 points ; Un trigone ou tri-côté ou tri-latère est un ensemble non ordonné de 3 droites. Triangle et trigone sont souvent confondus car ils sont duaux l'un de l'autre, cette tolérance de langage ne prête pas à conséquence.
En revanche, un quadrangle complet est un ensemble non ordonné de 4 points, il donne naissance à 6 côtés et 3 points diagonaux ; un quadrilatère complet est un ensemble non ordonné de 4 droites, il donne naissance à 6 sommets et 3 droites diagonales.
La même nuance est valable pour distinguer un hexagone d'un hexangle lorsqu'il y a un risque de confusion.

Du plan fondamental vers Pappus

Ce théorème s'énonce ainsi :

Un plan projectif fondamental (PPF) est pappusien (PPP).

Il se démontre en utilisant une transformation unidimensionnelle identité judicieusement choisie.

Plan projectif fondamental

Un plan projectif fondamental (PPF) est un plan proejctif qui vérifie l’axiome fondamental de la géométrie projective, donc au total les axiomes :

Il existe au moins 2 points.
Chaque droite possède au moins 3 points.
Pour deux points distincts il existe une et une seule droite qui leur est incidente.
Deux droites distinctes ont un et un seul point commun.
Pour toute droite il existe au moins un point non incident à cette droite.
Axiome fondamental : une transformation projective unidimensionnelle d'une droite sur elle-même qui comporte trois points fixes est l'identité projective unidimensionnelle.

Du plan homogène vers le fondamental

Ce théorème s'énonce ainsi :

Un plan projectif homogène (PPH) est fondamental (PPF).

Remarque : ce théorème utilise les propriétés algébriques du corps commutatif K.

Démonstration homogène---fondamental

On considère dans un PPhomogène une transformation projective unidimensionnelle d'une droite sur elle-même qui comporte trois points fixes. Est-elle l'identité projective unidimensionnelle ?

Soient la droite (u ; v ; w), trois de ses points P1 = [ wD ; wE ; -(uD+vE) ], P2 = [ wL ; wM ; -(uL+vM) ], P3 = [ w (D + hL) ; w (E + hM) ; -(uD+vE) -h(uL+vM) ] et une transformation projective unidimensionnelle T de formule générale (cas où w est non nul) :

T={\begin{bmatrix}vww(vc'+wb')&-uvwwc&-uvwwb\\-uvwwc'&wuw(wa'+uc)&-uvwwa\\-uvwwb'&-uvwwa'&uvw(ub+va)\end{bmatrix}}.

L'expression que les trois points P1, 2 et 3 sont fixes conduit à trois équations dont les inconnues sont a b c a' b' c' :

(uv^{2}a+wu^{2}c+uw^{2}a')*DE-(u^{2}vb+vw^{2}b'+v^{2}wc')*DE+(u^{2}va-uvwc')*D^{2}-(uv^{2}b-uvwc)*E^{2}=0

(uv^{2}a+wu^{2}c+uw^{2}a')*LM-(u^{2}vb+vw^{2}b'+v^{2}wc')*LM+(u^{2}va-uvwc')*L^{2}-(uv^{2}b-uvwc)*M^{2}=0

(uv^{2}a+wu^{2}c+uw^{2}a')*(D+hL)(E+hM)-(u^{2}vb+vw^{2}b'+v^{2}wc')*(D+hL)(E+hM)+(u^{2}va-uvwc')*(D+hL)^{2}-(uv^{2}b-uvwc)*(E+hM)^{2}=0

Qui conduisent dans une première étape, en posant pour des raisons d'homogénéïté deux nombres arbitraires k^3, g=1, à 4 nouvelles équations où les variables (D E L M h) des coordonnées des 3 points sont éliminées :

(uv^{2}a+wu^{2}c+uw^{2}a')=k^{3}g=(u^{2}vb+vw^{2}b'+v^{2}wc')

(u^{2}va-uvwc')=0

(uv^{2}b-uvwc)=0

. Ce qui conduit à definir les paramètres c a' b' c' par

wc=vb

uw^{2}a'=k^{3}g-uv(va+ub)

vb'=ua'

wc'=ua

La transformation qui conserve les trois points fixes sur la droite s'écrit alors :

N={\begin{bmatrix}wk^{3}g-uvwub&-uvwvb&-uvwwb\\-uvwua&wk^{3}g-uvwva&-uvwwa\\-uk^{3}g+uvu(va+ub)&-vk^{3}g+vuv(va+ub)&uvw(va+ub)\end{bmatrix}}.

Un point quelconque de la droite concernée est P = [wX ; wY ; -(uX+vY)] et on vérifie que N*P=w*k^3*g*P, tous les points de la droite sont donc fixes.

Il s'agit de la transformation identité (N) sur cette droite ; par conséquent le plan homogène respecte l'axiome fondamental du plan projectif fondamental. Ainsi il est démontré qu'« un plan projectif homogène (PPH) est fondamental (PPF) ».

Remarque : après ce théorème démontré nécessairement par une méthode de géométrie analytique, quasiment toute la suite de l'étude de la géométrie projective pourra se faire sans calculs analytiques.

Depuis Désargues vers les coniques

Parvenus à ce point, on peut introduire les coniques. L'approche des coniques peut être fondée sur le théorème de Pascal. Plusieurs définitions des coniques peuvent être adoptées :

en termes de courbes du second degré.
en termes d'intersection d'un cône et d'un plan. C'était la définition bimillénaire, voir conique.
en termes de faisceaux de droites en correspondance homographique.
en termes de birapport constant.
en termes de courbe autoduale, comme le fait H.S.M. Coxeter.

On peut adopter une discipline axiomatique.

Questions soulevées par l'explosion combinatoire

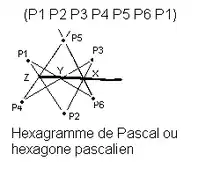
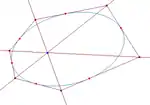
Si l'on observe la configuration de Désargues, on constate que 4 couples de triangles peuvent être créés. En plus de ABC-A'B'C' sur lequel on a coutume de travailler, il y a aussi ABC'-A'B'C, AB'C'-A'BC et AB'C-A'BC' qui donnent 3 nouvelles droites de Désargues, d'où un quadrilatère complet ; de plus, la même étude combinatoire menée sur le théorème dual conduit à 4 triangles qui donnent, outre le point O, 3 autres points de convergence des côtés, d'où un quadrangle complet. Quelles sont les propriétés de ce quadrangle et de ce quadrilatère, comment se déduisent-ils l'un de l'autre ? La configuration de Pappus offre une plus forte permutation ; il y a 6 hexagrammes non dégénérés (A1 C2 B1 A2 C1 B2, dessiné ci-contre ; A1 C2 B1 B2 C1 A2 ; A1 B2 B1 C2 C1 A2 ; A1 B2 B1 A2 C1 C2 ; A1 A2 B1 B2 C1 C2 ; A1 A2 B1 C2 C1 B2 ;), donc 6 droites de Pappus. Quelles sont les propriétés de ces 6 droites ? En fait on peut démontrer qu'elles sont concourantes en deux groupes de 3. Mais de quels axiomes minimaux a-t-on besoin pour démontrer cette propriété ? L'axiome Fondamental de la géométrie projective est-il indispensable ? l'axiome de Désargues suffirait-il ? Quant à l'hexagramme de Pascal, de nombreux mathématiciens du XIX^e siècle se sont penchés sur les diverses permutations du parcours des 6 points. Il s'agit particulièrement de Bauer, Catalan, Cayley, Fontaneau, Gräfe, Grossmann, Hesse, Jörres, Kirkman, Ladd-Franklin-Christine, Little, Lüroth, Meyer, Molk, Plücker, Salmon, Jakob Steiner, Veronese-G., von Staudt. Avec 6 points, on peut réaliser 60 parcours hexagonaux, donc 60 droites de Pascal. Quelles sont les propriétés de ces 60 droites, comment sont disposées leurs intersections dans le plan ? Quel rapport avec les 60 points de Brianchon que l'on peut dualement envisager ? Par exemple Steiner a montré qu'elles sont concourantes 3 à 3, d'où 20 « points de Steiner ».

Notes et références

Jacqueline Lelong-Ferrand, p. 186-187
Veblen & Young 1910 chapitre 6 pour les détails ; la référence à von Staudt est donnée p. 141 (éd. 1918).
Par exemple Coxeter 1969, p. 233
Artin 1957 chap. ?
voir (en) H. S. M. Coxeter, « Self-dual configurations and regular graphs », Bull. Amer. Math. Soc., vol. 56,‎ 1950 (lire en ligne) page 432, ou Coxeter 1969, p. 236.
Veblen & Young 1910, p. 95 (édition 1918) ou Coxeter 1987, p. ?.
Veblen & Young 1910, chapitre VI page 148 de l'édition 1918, chapitre V pour l'étude des coniques, ainsi que Coxeter 1987.

Bibliographie

Emil Artin, Algèbre géométrique, Calmann-Lévy, traduction de Geometric algebra New York, Interscience Publishers, Inc., 1957.
(en) Rey Casse, Projective Geometry : An Introduction, Oxford University Press, 2006, 198 p. (ISBN 0-19-929885-8, lire en ligne).
(en) H. S. M. Coxeter, Projective Geometry, Springer Verlag, 1987, 2^e éd., 162 p. (ISBN 0-387-40623-9, lire en ligne).
(en) H. S. M. Coxeter, Introduction to Geometry, 1969, 2^e éd. [détail de l’édition]
Jacqueline Lelong-Ferrand, Fondements de la géométrie, Paris, PUF, 1985, 287 p. (ISBN 2-13-038851-5).
(en) Oswald Veblen et John Wesley Young, Projective geometry Volume I, Ginn and Co., Boston, 1910 (ISBN 978-1-4181-8285-4, MR 0179666, lire en ligne), 2^de édition 1918, lien.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.