Parallélogramme
En géométrie, un parallélogramme est un quadrilatère dont les segments diagonaux se coupent en leur milieu[1].
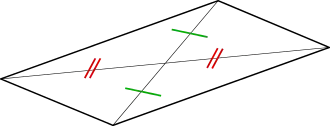
Définitions équivalentes
En géométrie purement affine, un quadrilatère (ABCD) est un parallélogramme (au sens défini en introduction) si et seulement s'il satisfait l'une des propriétés équivalentes suivantes :
- les vecteurs et sont égaux ;
- les vecteurs et sont égaux.
Si de plus les quatre sommets sont trois à trois non alignés, ces propriétés sont aussi équivalentes à la suivante : les côtés opposés sont parallèles deux à deux, c'est-à-dire : (AB) // (CD) et (AD) // (BC)[2].
En géométrie euclidienne, sous cette même hypothèse, ces propriétés sont aussi équivalentes à :
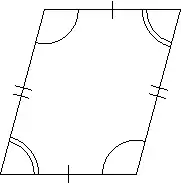
- le quadrilatère est non croisé et ses côtés opposés sont de même longueur deux à deux ;
- il est convexe et ses angles opposés ont la même mesure deux à deux ;
- ses angles consécutifs sont supplémentaires deux à deux ;
- c'est un trapèze (non croisé) dont les bases ont même longueur.
Propriétés
- Tout parallélogramme a un centre de symétrie : le point d'intersection de ses diagonales.
- Dans tout parallélogramme ABCD, on a l'identité du parallélogramme : AC2 + BD2 = 2(AB2 + BC2).
- Les angles d'un parallélogramme qui se suivent sont supplémentaires
- Les angles opposés sont égaux
Cas particuliers
- Un losange est un parallélogramme ayant au moins deux côtés consécutifs de même longueur[1]. Il est même équilatéral.
- Un rectangle est un parallélogramme ayant au moins un angle droit. Il est même équiangle.
- Un carré est un losange rectangle.
Aire

Soient la longueur d'un côté du parallélogramme et la longueur de la hauteur associée. L'aire du parallélogramme vaut :
L'aire d'un parallélogramme est aussi donnée par un déterminant.
Antiparallélogramme
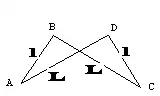
Un antiparallélogramme est un quadrilatère croisé dont les côtés opposés ont la même longueur deux à deux.
Dans un antiparallélogramme, les angles opposés ont la même mesure en valeur absolue.
Équipollence et vecteurs
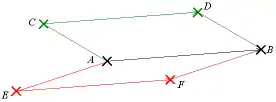
Il est désormais classique de définir la notion de parallélogramme à partir de celle de vecteur (voir supra) mais on peut inversement, à partir de la notion de milieu, définir (comme en introduction) celle de parallélogramme, puis celle d'équipollence de deux bipoints, et enfin celle de vecteur :
- on appelle bipoint tout couple de points (l'ordre des points a une importance) ;
- deux bipoints (A, B) et (C, D) sont dits équipollents si ABDC est un parallélogramme ;
- La relation d'équipollence est une relation d'équivalence.
- on appelle vecteur la classe d'équivalence du bipoint (A,B), c'est-à-dire l'ensemble des bipoints équipollents à (A,B).
On retrouve alors qu'un quadrilatère (ABCD) est un parallélogramme si et seulement si .
Voir aussi
- Aire d'un polygone
- Parallélépipède
- Paralléloèdre (en)
- Parallélogone (en)
- Théorème de Varignon
Notes et références
- M. Troyanov, Cours de géométrie, PPUR, 2002, p. 13.
- Jean Dieudonné, Algèbre linéaire et géométrie élémentaire, Hermann, , exercice 1, p. 50.








