Cerf-volant (géométrie)
En géométrie, un cerf-volant est un quadrilatère dont une des diagonales est un axe de symétrie (ou — ce qui est équivalent — un quadrilatère formé de deux paires de côtés adjacents égaux). Les diagonales peuvent se couper à l'intérieur (cerf-volant convexe) ou à l'extérieur (« pointe de flèche » ou cerf-volant non convexe). Ceci contraste avec un parallélogramme, où les côtés égaux sont opposés. L'objet géométrique est nommé en référence au cerf-volant que l'on fait voler, qui a, dans son aspect le plus simple, la forme d'un cerf-volant convexe.
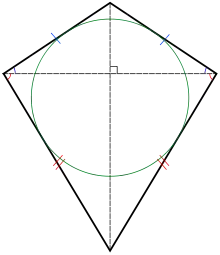

Propriétés
- La diagonale qui est un axe de symétrie divise le cerf-volant en deux triangles isométriques.
- Elle est la médiatrice de l'autre diagonale.
- Un cerf-volant convexe est circonscriptible et possède donc un cercle inscrit, c'est-à-dire qu'il existe un cercle qui est tangent aux quatre côtés.
- Si et sont les longueurs des diagonales, alors l'aire est (comme dans tout quadrilatère orthodiagonal)
- Alternativement, si et sont les longueurs des côtés, et l'angle entre les côtés inégaux, alors l'aire est
- Dans un cerf-volant convexe, la diagonale qui n'est pas l'axe de symétrie, divise le cerf-volant en deux triangles isocèles.
Cas particuliers
Si tous les côtés sont de la même longueur et si les quatre sommets sont distincts, le quadrilatère est un losange.
Les cerfs-volants inscriptibles (c'est-à-dire dont les quatre sommets sont cocycliques) sont ceux à deux angles droits (en).
Les cerfs-volants construits par juxtaposition de deux triangles d'or permettent de réaliser des pavages de Penrose de second type (P2).
Voir aussi
- (en) Kite (définition et propriétés, avec une animation interactive)
- (en) Area of a kite (aire : formules et animation interactive)
- Patrice Debart, « Cerf-volant (géométrie) », sur Descartes et les Mathématiques






