Quadrilatère inscriptible

Théorème de Sturm [4] - [5]: s'il existe un quadrilatère de longueurs de côtés successifs ${\displaystyle a,b,c,d}$, c'est-à-dire si ${\displaystyle a\leqslant b+c+d,b\leqslant c+d+a,c\leqslant d+a+b,d\leqslant a+b+c}$, alors il existe un quadrilatère convexe inscriptible ayant ${\displaystyle a,b,c,d}$ pour longueurs de côtés.

Cela signifie que les sommets de tout quadrilatère articulé peuvent être inscrits dans un cercle.

L'aire S d'un quadrilatère convexe inscriptible en fonction des longueurs a, b, c et d de ses côtés successifs est donnée par la formule de Brahmagupta :

${\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}$

où p = a + b + c + d/2 est le demi-périmètre.

D'après la formule de Bretschneider, un quadrilatère convexe ayant a, b, c d pour suite de longueurs des côtés possède une aire maximale lorsqu'il est inscriptible.

L'aire d'un quadrilatère convexe inscriptible est aussi donnée (voir infra) par :

${\displaystyle S={\frac {1}{2}}(bc+ad)\sin \gamma }$

où γ est l'angle entre les côtés de longueurs a et d.

Le théorème de Ptolémée dit que le produit des longueurs e et f des deux diagonales d'un quadrilatère convexe inscriptible est égal à la somme des produits des longueurs des côtés opposés ac et bd :

${\displaystyle ef=ac+bd}$.

Les deux diagonales d'un quadrilatère convexe le coupent en quatre triangles ; lorsque le quadrilatère est inscriptible, les paires de triangles opposés sont constituées chacune de deux triangles semblables.

Pour un quadrilatère convexe inscriptible de sommets successifs A, B, C, D, de côtés successifs a = AB, b = BC, c = CD et d = DA, et de diagonales e = AC et f = BD, on a (second théorème de Ptolémée):

${\displaystyle {\frac {e}{f}}={\frac {ad+cb}{ab+cd}},\quad e^{2}={\frac {(ac+bd)(ad+bc)}{ab+cd}}\quad {\text{et}}\quad f^{2}={\frac {(ac+bd)(ab+dc)}{ad+bc}}.}$

Si le point d'intersection des diagonales divise une diagonale en segments de longueurs ${\displaystyle e_{1}}$ et ${\displaystyle e_{2}}$, et divise l'autre diagonale en segments de longueurs ${\displaystyle f_{1}}$ et ${\displaystyle f_{2}}$, alors ${\displaystyle e_{1}e_{2}=f_{1}f_{2}}$. (Ceci est valable parce que les deux diagonales sont des cordes d'un cercle.)

Tout rectangle est un trapèze isocèle, c'est-à-dire un trapèze circonscriptible. Un cerf-volant est inscriptible si et seulement s'il a deux angles droits.

• Durant le XIV^e siècle, le mathématicien Parameshvara Nambudiri (en) détermina le rayon du cercle circonscrit d'un quadrilatère inscriptible. Notons les longueurs des côtés successifs a, b, c, d, le demi-périmètre p et l'aire S ; le rayon R s'obtient par la formule[6] :

${\displaystyle R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(p-a)(p-b)(p-c)(p-d)}}}={\frac {\sqrt {(ab+cd)(ac+bd)(ad+bc)}}{4S}}}$.

• Il n'existe pas de quadrilatère inscriptible dont l'aire est rationnelle et dont les longueurs des côtés sont rationnelles, inégales et forment une progression arithmétique ou géométrique[7].

• Les fonctions trigonométriques de l'angle γ entre les côtés de longueurs a et d sont données par[8] :

${\displaystyle \cos \gamma ={\frac {a^{2}+d^{2}-b^{2}-c^{2}}{ad+bc}}}$ ;

${\displaystyle \sin \gamma ={\frac {2S}{ad+bc}}}$ (S étant l'aire) ;

${\displaystyle \tan {\frac {\gamma }{2}}={\sqrt {\frac {(p-a)(p-d)}{(p-b)(p-c)}}}}$.

• Théorème de Jules Mathot (1901) : Dans un quadrilatère convexe inscriptible, les quatre droites passant par le milieu d'un côté et perpendiculaires au côté opposé sont concourantes. Le point de concours est le symétrique H du centre O du cercle circonscrit par rapport au centre de gravité G [9]^{p. 131} - [10] - [11].

Ces quatre droites sont appelées "maltitudes" en anglais (pour "midpoint-altitude"), ce que l'on peut traduire par "hauteurs médianes".

Certains auteurs considèrent la droite (OGH) comme la "droite d'Euler" du quadrilatère inscriptible [1].

• Théorème japonais

Dans un quadrilatère orthodiagonal (c'est-à-dire dont les diagonales sont perpendiculaires), les "hauteurs médianes" définies ci-dessus se coupent deux à deux sur des diagonales. Par exemple, les "hauteurs médianes" issues des milieux de [AD] et [AB] se coupent sur la diagonale issue de A.

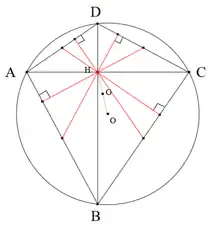
Par conséquent, d'après la propriété ci-dessus, dans un quadrilatère à la fois inscriptible et orthodiagonal, les quatre "hauteurs médianes" concourent au point d’intersection H des diagonales, appelé l'anticentre du quadrilatère inscriptible orthodiagonal [1].

On retrouve ainsi le théorème de Brahmagupta, affirmant que dans un quadrilatère inscriptible orthodiagonal, la perpendiculaire à n'importe quel côté passant par le point d'intersection des diagonales coupe l'autre côté en son milieu[9]^{p. 137}.

Dans un quadrilatère inscriptible orthodiagonal :

• la distance du centre O du cercle circonscrit à n'importe quel côté est égal à la moitié de la longueur du côté opposé[9]^{p. 138},

• supposons que l'intersection des diagonales divise une diagonale en segments de longueurs e₁ et e₂ et divise l'autre diagonale en segments de longueurs f₁ et f₂. Alors[13]

${\displaystyle e_{1}^{2}+e_{2}^{2}+f_{1}^{2}+f_{2}^{2}=a^{2}+c^{2}=b^{2}+d^{2}=D^{2}}$

où D est le diamètre du cercle circonscrit. Cela est dû au fait que les diagonales sont des cordes perpendiculaires d'un cercle. De façon équivalente, soit R = ^D⁄₂ le rayon du cercle circonscrit, la moyenne de e₁², e₂², f₁² et f₂² est R². En outre, les équations a² + c² = b² + d² = D² impliquent que la somme des carrés des côtés est égal à huit fois le carré du rayon du cercle circonscrit.

Le quotient du périmètre d'un cercle par celui d'un carré inscrit est égal à π/2√2 ≈ 1,110 720 (suite A093954 de l'OEIS).