Sommet (géométrie)
En géométrie, un sommet est un point particulier d'une figure :
- un sommet d'un polygone, d'un polyèdre, ou plus généralement d'un polytope, est un 0-simplexe de celui-ci ;
- c'est l'extrémité d'au moins une arête (par analogie, on parle aussi de sommets en théorie des graphes) ;
- dans un polyèdre, en chaque sommet, au moins trois faces et un nombre égal d'arêtes se coupent (voir aussi le théorème de Descartes-Euler, qui lie le nombre de sommets d'arêtes et de faces d'un polyèdre) ;
- le sommet d'un angle est le point d'intersection des deux côtés de cet angle ;
- le sommet d'un cône est le point d'intersection de toutes les génératrices de ce cône.
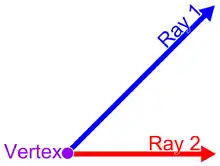
Le sommet d'un angle est le point d'intersection où se réunissent deux segments de lignes .
Principaux sommets
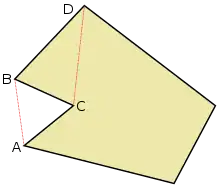
Le sommet B est une « oreille », parce que la ligne droite entre C et D est entièrement à l'intérieur du polygone. Le sommet C est une « bouche », parce que la ligne droite entre A et B est complètement à l'extérieur du polygone (Définition à vérifier).
Voir aussi
- apex, un ou plusieurs sommets distingués des autres dans une figure (selon un axe de projection et de mesure)
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.