Théorème des fonctions implicites
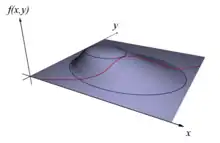
En mathématiques, le théorème des fonctions implicites est un résultat de géométrie différentielle. Certaines courbes planes sont définies par une équation cartésienne, c'est-à-dire une équation de la forme f(x, y) = 0, où x et y décrivent les nombres réels. Le théorème indique que si la fonction f est suffisamment régulière au voisinage d'un point de la courbe, il existe une fonction φ de ℝ dans ℝ au moins aussi régulière que f telle que localement, la courbe et le graphe de la fonction φ sont confondus. Plus précisément, si (x0, y0) vérifie l'équation, si f est continûment différentiable et si sa dérivée partielle par rapport à y en (x0, y0) n'est pas nulle alors, au voisinage de (x0, y0), la courbe s'identifie au graphe de φ.
Ce théorème admet une variante plus générale, qui s'applique non plus au plan, mais à des espaces de Banach, c'est-à-dire des espaces vectoriels normés complets. Il équivaut au théorème d'inversion locale, qui indique qu'une fonction différentiable et « suffisamment régulière » est localement inversible (c'est une conséquence directe d'un théorème du point fixe).
Ce théorème est utilisé dans différentes branches des mathématiques, sous cette forme ou sous celle de l'inversion locale. Il permet de démontrer le théorème des extrema liés ; il intervient dans un contexte plus géométrique, pour l'étude des sous-variétés différentielles ; on le trouve encore pour l'étude des équations différentielles où il est, entre autres, utilisé à travers le théorème du redressement d'un flot, permettant de démontrer le théorème de Poincaré-Bendixson. Il dépasse le cadre des mathématiques : les physiciens ou les économistes en font usage, lorsque certaines variables ne peuvent être définies à l'aide d'une fonction, mais uniquement implicitement à l'aide d'une équation.
Dimension 2
Avant d'énoncer le théorème sous sa forme générale, prenons l'exemple de la dimension 2 :
Soit f une fonction de classe Cp (avec p > 0) définie sur un ouvert U de ℝ2 et à valeurs dans ℝ. Soit (x0, y0) un point de U tel que f(x0, y0) = 0 et tel que la dérivée partielle de f par rapport à la deuxième variable ne soit pas nulle en (x0, y0). Il existe une fonction réelle de classe Cp, définie sur un intervalle ouvert réel V contenant x0, et un voisinage ouvert Ω de (x0, y0) dans U tels que, pour tout (x, y) ∈ ℝ2 :
.
La condition n'est pas explicitée car elle n'est qu'un cas particulier de l'équivalence. La dérivée de au point x0 est donnée par la formule :
Des exemples sont détaillés dans l'article « Fonction implicite ».
Énoncé
Il est utile d'étendre ce résultat sur des surfaces et non plus sur des courbes, voire sur des espaces vectoriels dont la dimension n'est pas nécessairement finie. On trouve cette version plus générale[1] - [2] :
Théorème des fonctions implicites — Soient E, F et G trois espaces de Banach et f une fonction de classe Cp définie sur un ouvert U de E × F et à valeurs dans G. Soit (x0, y0) un point de U tel que f(x0, y0) = 0 et tel que la différentielle partielle Dyf(x0, y0) soit inversible[Note 1]. Il existe une fonction φ de classe Cp à valeurs dans F, définie sur un voisinage ouvert V de x0, et un voisinage ouvert Ω de (x0, y0) dans U tels que, pour tout (x, y) ∈ E×F :
Remarques
- L'existence d'un tel ouvert Ω signifie que le graphe de φ est un ouvert de l'ensemble des zéros de f, ce qui garantit automatiquement l'unicité de φ, au sens suivant[3] :Sur toute partie connexe C de V contenant x0, φ est la seule application continue vérifiant
Dimension supérieure
Multiplicateur de Lagrange
Le théorème des fonctions implicites peut aussi être vu comme un outil pour démontrer des résultats, comme le théorème des extrema liés. On se place ici sur un ouvert U d'un espace de Banach E et l'on cherche les extrema d'une fonction f restreinte à un sous-ensemble S ⊂ U défini par une contrainte g(x) = 0, où f : U → R et g = (g1, … , gm) : U → Rm sont supposées continument différentiables et la différentielle dg(a) en chaque point a de S est supposée surjective.
Le théorème des extrema liés[Note 2] indique qu'en chaque point a de S où f est extrémale, la différentielle de f est une combinaison linéaire des différentielles des gi. Le théorème des fonctions implicites permet de montrer simplement ce résultat[Note 2], en considérant localement S comme le graphe d'une fonction φ définie sur un ouvert V du noyau de dg(a). Le problème se ramène ainsi à l'étude des extrema ordinaires de la fonction z ↦ f(z, φ(z)), et l'on sait qu'une condition nécessaire d'extremum en un point de V est la nullité de la différentielle de cette fonction en ce point. C'est en répercutant sur f et g cette condition qu'on aboutit au résultat.
Variété différentielle
Une sous-variété différentielle de dimension d de Rn où n et d sont des entiers tels que 0 < d < n, permet de généraliser les notions de courbes ou de surfaces « lisses et régulières » de dimension 2. Les termes de « lisse et régulier » sont des métaphores pour désigner le fait que les objets considérés n'ont pas d'arête ou de point double. L'objet de ce paragraphe concerne les figures à l'image d'une sphère, qui est une variété différentielle de dimension 2, mais pas d'un cube, qui contient des points singuliers[Note 3].
Le voisinage d'un point O dans une sous-variété M de dimension d de Rn possède la propriété d'être semblable, au sens du difféomorphisme, à un ouvert de Rd. On peut l'exprimer de la manière suivante : il existe un homéomorphisme φ1, continument différentiable de Rd dans un ouvert de M contenant le point O et la différentielle de φ1 en un point quelconque est de rang d. Autrement dit, il existe un « bon » paramétrage d'un voisinage de O dans M. Il est aussi possible d'exprimer cette propriété à l'aide d'une équation cartésienne. Il existe un ouvert V de Rn et une fonction ψ de V dans Rn–d continument différentiable et dont les différentielles sont surjectives, tels que M∩V soit l'ensemble des points x qui vérifient l'équation ψ(x) = 0, ce qui donne une définition locale à l'aide d'une équation cartésienne[7] - [8].
L'équivalence de ces deux points de vue se démontre dans un sens avec le théorème des fonctions implicites, la réciproque est plus aisée avec le théorème d'inversion locale.
Supposons que l'on dispose d'une équation paramétrique ψ1(x) = 0 sur le voisinage U. La différentielle de ψ1 en x0, coordonnées du point O, est de rang d et possède un noyau K de dimension n - d et un supplémentaire H de ce noyau de dimension d, d'après le théorème du rang. Tout élément de U s'écrit de manière unique comme égal à une somme x0 + h + k et l'on peut choisir un ouvert UH de H contenant le vecteur nul et un ouvert UK de H contenant le vecteur nul tel que x0 + UH + UK soit contenu dans U. L'application ψ de UH×UK dans Rd, qui à (h, k) associe ψ1(x0 + h + k) satisfait aux hypothèses du théorème des fonctions implicites, d'où l'existence d'un paramétrage locale du voisinage de O, construit sur le voisinage UH.
.jpg.webp)
On suppose maintenant que l'on dispose d'une représentation paramétrique locale du voisinage de O, c'est-à-dire une application φ1 de Rd dans Rn dont l'image est un voisinage de O dans la variété. Cette situation est illustrée sur la figure de droite. La droite bleue représente Rd, la portion de courbe la variété contenant le point O est représentée en rouge. On identifie Rd avec le sous-espace vectoriel de Rn dont les n - d dernières coordonnées sont nulles. L'image de la différentielle de φ1 au point x0 est un sous-espace vectoriel de dimension d, on considère Ha un supplémentaire de ce sous-espace vectoriel. On appelle Hd le sous-espace de Rn ayant les d premières coordonnées nulles. Les sous-espaces Ha et Hd ayant même dimensions, ils sont isomorphes ; soit φ2 un tel isomorphisme. On considère maintenant l'application φ de U×Hd dans Rn, qui à x0 + h + k associe φ1(x0 + h) + φ2(k). Ici, h désigne un vecteur de Rd et k un vecteur de Ha. L'application φ est continument différentiable et sa différentielle au point x0 est un isomorphisme. Le théorème d'inversion locale montre qu'il existe un ouvert W contenant O et une application ψ1 de W dans Rn différentiable et qui soit localement une réciproque de φ. L'image de l'intersection de la variété et de W est incluse dans Hd, si l'ouvert W est choisi suffisamment petit. Il suffit, pour conclure, de composer ψ1 par l'application linéaire qui, à un vecteur de Rn, associe le vecteur de Rn–d constitué des n - d dernières coordonnées du vecteur d'origine. Si ψ est cette application composée, sur un voisinage de O, la variété est définie par l'équation ψ(x) = 0.
Théorème du redressement d'un flot
Le théorème des fonctions implicites joue un rôle pour l'étude des équations différentielles. On le trouve à divers endroits, dont le théorème du redressement d'un flot[9]. Considérons l'équation différentielle autonome (1) :
Ici f désigne une fonction continument différentiable définie sur U, un ouvert d'un espace de Banach E et à valeurs dans E. Le théorème de Cauchy-Lipschitz montre l'existence d'une unique fonction flot φ qui prend ses valeurs dans un ouvert V inclus dans R×U et à valeurs dans E, telle que la fonction qui à t associe φ(t, x) soit l'unique solution de l'équation (1) avec la condition de Cauchy s(0) = x.
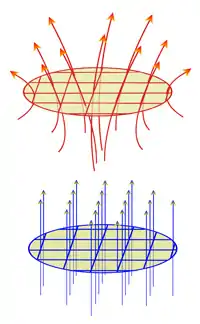
Un exemple de flot, au voisinage V1 d'un point x0 de U est illustré en rouge à droite. Si l'on considère l'intersection de V1 avec un hyperplan affine contenant x0 et dont la direction ne contient pas f(x0), on obtient la « pastille » illustrée en rouge et jaune. Pour l'étude locale d'un flot, la configuration équivalente au-dessous, en bleu est plus simple. Si la fonction f est constante, sur un voisinage de la pastille V, pour un point x de V, les solutions de l'équation différentielle (1) sont décrites par le flot φ(t, x) = x + tv où v est le vecteur constant image de f, sur un voisinage de V.
Une conséquence du théorème du redressement est l'existence d'un difféomorphisme ψ défini sur un voisinage W de x tel que :
Autrement dit, il est possible de « redresser » le flot φ à l'aide d'un difféomorphisme ψ, ce qui permet une étude locale plus aisée de l'équation différentielle (1). La démonstration de ce résultat est fondée sur le fait que la fonction flot est aussi continument différentiable. La restriction de φ à W×]–μ, μ[ possède au point (0, x0) une différentielle inversible[Note 1]. Le théorème d'inversion locale permet de conclure. Ce résultat est utilisé, par exemple dans la démonstration du théorème de Poincaré-Bendixson[10].
Théorème de Cauchy-Lipschitz
Le théorème précédent est une application directe du théorème d'inversion locale, à la condition de disposer d'un résultat non immédiat. Si la fonction f du paragraphe précédent est de classe C1, alors le flot l'est aussi. Ce résultat porte généralement le nom de théorème de Cauchy-Lipschitz. Cette forme sophistiquée du théorème est traitée dans l'article détaillé. De manière indépendante, deux mathématiciens Pugh et Robbin[11] ont trouvé une même démonstration élémentaire. Elle consiste à étudier l'application T qui à un couple (x, σ) associe une fonction. Ici x est un élément de U avec les notations du paragraphe précédent et σ une fonction d'un petit intervalle contenant O. L'application est définie de la manière suivante :
La solution intégrale s, qui à t associe φ(t, x) vérifie l'égalité T(x, s) = 0. Il est relativement simple de montrer que T satisfait les hypothèses du théorème des fonctions implicites, ce qui montre que la fonction qui à x associe la courbe intégrale φ(t, x) est de classe C1. À partir de là, il est simple d'en déduire le caractère C1[Note 2].
Cette démonstration montre la pertinence du deuxième énoncé, très général, du théorème des fonctions implicites proposé dans cet article. En analyse fonctionnelle et à l'image du résultat de ce paragraphe, il est utile de pouvoir choisir les variables dans un Banach.
Théorème des fonctions implicites holomorphes
Si on s'intéresse aux fonctions holomorphes à une ou plusieurs variables, on dispose d'une variante du théorème des fonctions implicites appelée théorème des fonctions implicites holomorphes[12].
Soient pour des fonctions holomorphes au voisinage d'un point telles que pour tout . Supposons que
Alors les équations
admettent une solution holomorphe au voisinage de telle que .
Notes et références
Notes
- Une application linéaire continue T : E → F entre deux espaces vectoriels normés est dite inversible lorsqu'elle est bijective et que sa réciproque T−1 : F → E (linéaire) est continue. Entre espaces de dimension finie, toute application linéaire est continue. Entre espaces de Banach, d'après le théorème de Banach-Schauder, la réciproque d'une bijection linéaire continue est toujours continue. François Laudenbach, Calcul différentiel et intégral, éd. École Polytechnique, , 214 p. (ISBN 978-2-7302-0724-9, lire en ligne), p. 49.
- Voir l'article détaillé.
- Pour une définition précise, voir l'article détaillé.
Références
- Pour une démonstration, voir par exemple .
- Robert Roussarie et Jean Roux, Des équations différentielles aux systèmes dynamiques, vol. I, EDP Sciences, (lire en ligne), p. 15, dans le cas d'espaces de dimension finie.
- Pour une démonstration, voir par exemple cet .
- Serge Lang, Analyse Réelle, Paris, InterÉditions, , 230 p. (ISBN 978-2-7296-0059-4), p. 122.
- Laudenbach 2000, p. 65.
- Dany-Jack Mercier, Fonctions de plusieurs variables réelles : exercices et problèmes corrigés, Publibook, (lire en ligne), p. 324, dans le cas d'espaces de dimension finie.
- Marcel Berger et Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions], § 2.1.
- F. Ronga, « Dérivabilité, théorème des fonctions implicites et applications », sur Université de Genève, p. 78.
- D. Leborgne, Calcul différentiel et géométrie, PUF, 1982, p. 234.
- C'est pour cette raison que ce résultat est présenté, par exemple dans Claude Viterbo, « Conjugaison, redressement et premier retour », sur École Polytechnique, .
- Lang 1977, p. 129.
- Henri Cartan, Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes, Hermann, , p. 138
Voir aussi
Article connexe
Bibliographie
(en) Michael Spivak, (A Comprehensive Introduction to) Differential Geometry [détail des éditions]






![{\displaystyle \forall x\in W,\;\forall t\in \left]-\mu ,\mu \right[\quad \psi \circ \varphi (t,x)=x+tv}](https://img.franco.wiki/i/0d5c13e78b17207639f9b9874c04b90e840bb963.svg)









