Dimension finie
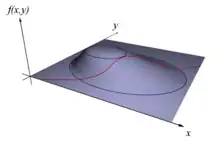
La méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure le point le plus élevé possible, tout en satisfaisant une contrainte, sur la figure un point de la ligne rouge.
On cherche à trouver l'extremum, un minimum ou un maximum, d'une fonction φ de n variables à valeurs dans les nombres réels, ou encore d'un espace euclidien de dimension n, parmi les points respectant une contrainte, de type ψ(x) = 0 où ψ est une fonction du même ensemble de départ que φ. La fonction ψ est à valeurs dans un espace euclidien de dimension m. Elle peut encore être vue comme m fonctions à valeurs réelles, décrivant m contraintes.
Si l'espace euclidien est de dimension 2 et si la fonction ψ est à valeurs dans ℝ, correspondant à une contrainte mono-dimensionnelle, la situation s'illustre par une figure analogue à celle de droite. La question revient à rechercher le point situé le plus haut, c'est-à-dire le maximum de φ, dans l'ensemble des points rouges, c'est-à-dire ceux qui vérifient la contrainte. Le point recherché est celui où la courbe rouge ne monte ni ne descend. En termes techniques, cela correspond à un point où la différentielle de ψ possède un noyau orthogonal au gradient de φ en ce point. La méthode du multiplicateur de Lagrange offre une condition nécessaire. Les fonctions φ et ψ sont différentiables et leurs différentielles continues ; on parle de fonction de classe C1. On considère λ un vecteur pris dans l'ensemble d'arrivée de ψ et la fonction L définie par :

Cette fonction est parfois appelée le lagrangien.
L'opérateur représenté par un point est ici le produit scalaire. Si x0 est une solution recherchée, on montre qu'il existe un vecteur λ0 tel que la fonction L admet une différentielle nulle au point (x0, λ0). Les coordonnées du vecteur λ0[2] — ou parfois du vecteur opposé[3] - [4] — sont appelées multiplicateurs de Lagrange. Cette technique permet de passer d'une question d'optimisation sous contrainte à une optimisation sans contrainte, celle de la fonction L, dans un espace de dimension n + m.
Exemple introductif
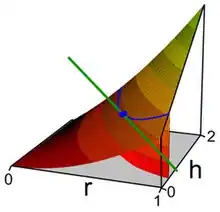
La nappe correspond à la surface du cylindre, la courbe bleue aux points de volume égal à v0, choisi dans la représentation égal à 1.
Soit v0 un nombre strictement positif. L'objectif est de trouver la portion de cylindre de rayon r et de hauteur h de surface minimale (couvercles compris) et de volume v0. Pour cela on définit deux fonctions, v et s qui à (r, h) associent respectivement le volume et la surface de la portion de cylindre. On dispose des égalités

La figure de droite représente la fonction s, qui à r et h associe la surface. La ligne bleue correspond aux points de volume égal à 1. L'objectif est de trouver le point bleu, de plus petite surface pour un volume égal à 1. La fonction s n'est autre que la fonction φ du préambule. La fonction ψ et la fonction L sont définies par :

La méthode de Lagrange consiste à rechercher un point tel que la différentielle de L soit nulle. Sur un tel point, la dérivée partielle par rapport à λ est nulle, ce qui signifie que la fonction ψ est nulle, ou encore que la contrainte est respectée. Si l'on identifie s avec son approximation linéaire tangente, son comportement sur la contrainte, aussi identifiée à son approximation linéaire tangente, est aussi nécessairement nulle à partir de l'ordre 1. Ce comportement est illustré par la droite en vert sur la figure. Le long de cette droite, la fonction ψ est nulle, et le terme d'ordre 1 de la fonction s l'est alors nécessairement.
Il suffit, en conséquence, de calculer la différentielle de L, et plus précisément ses trois dérivées partielles, pour l'exemple choisi :

On trouve les valeurs suivantes :

Autrement dit :
 et
et  , d'où
, d'où  .
.
Cet exemple possède l'avantage d'une représentation graphique simple, guidant l'intuition. En revanche, la méthode du multiplicateur de Lagrange n'est pas nécessaire dans ce cas : on peut simplement exprimer la valeur de h pour que le volume du cylindre respecte la contrainte imposée au volume v0. On trouve :

En "injectant" cette contrainte dans l'équation décrivant l'aire, il vient :

et il suffit de trouver la valeur de r minimisant cette fonction pour trouver la solution.
De même qu'avec le multiplicateur de Lagrange, on trouve :

Deuxième exemple : l'isopérimétrie du triangle
Pour se convaincre de la pertinence de la méthode, on peut rechercher le triangle d'aire maximale et de périmètre p, choisi strictement positif. D'après la formule de Héron, si (x, y, z) est le triplet des longueurs des côtés du triangle, son aire A est égale à :

Il est plus simple de maximiser la fonction φ qui associe à (x,y,z) quatre fois le carré de A. La contrainte est donnée par la fonction ψ qui associe au triangle la différence du périmètre et de p :
![{\displaystyle \varphi (x,y,z)={\frac {1}{4}}\left[(x^{2}+y^{2}+z^{2})^{2}-2(x^{4}+y^{4}+z^{4})\right]\quad {\text{et}}\quad \psi (x,y,z)=x+y+z-p.}](https://img.franco.wiki/i/7114803a3fc47a8b9b8be8f9e780c3ab8d697cdd.svg)
Un triangle n'est défini, pour un triplet (x, y, z), que si les trois coordonnées sont positives et si la somme de deux coordonnées est supérieure à la troisième. Soit D cet ensemble de points. Sur la frontière de D, la fonction φ est nulle. On cherche un point de l'intérieur de D tel que φ soit maximal dans l'ensemble des points d'image par ψ nulle. Comme l'intersection de l'image réciproque de 0 par ψ et de D est un compact, il existe au moins un maximum. On définit comme dans l'exemple précédent la fonction L par :

On cherche x, y, z strictement positifs et λ tels que la différentielle de L soit nulle. Un calcul de dérivée partielle montre que ce quadruplet est solution du système d'équations :

On vérifie alors que la seule solution est  , correspondant au triangle équilatéral.
, correspondant au triangle équilatéral.
- Remarque
- L'objectif est ici d'illustrer la méthode du multiplicateur de Lagrange. On a trouvé le maximum d'une fonction φ dans l'intérieur de D, sous la contrainte définie par ψ. Si l'objectif est uniquement de résoudre le problème isopérimétrique pour le triangle, une solution plus simple est donnée dans l'article sur l'isopérimétrie.
Notations et interprétation géométrique
Soient E et F deux espaces vectoriels réels de dimensions respectives n et m avec n plus grand que m. Soit φ une fonction de E dans ℝ, que l'on cherche à minimiser : on cherche un point a tel que φ(a) soit le plus petit possible. Soit ψ une fonction de E dans F, définissant la contrainte. L'ensemble sur lequel on travaille est G, correspondant aux points x tels que ψ(x) = 0.
Si (e1, … , en) est une base de E, chaque point x de E s'exprime comme une combinaison linéaire des éléments de la base :

Cette remarque permet de voir les fonctions φ et ψ de deux manières. Elles peuvent être vues comme des fonctions d'une unique variable x de E, ce qui rend l'écriture plus concise et favorise une compréhension plus simple, mais plus abstraite des mécanismes en jeu. Les applications peuvent aussi être vues comme fonctions de n variables x1, … , xn, ce qui présente une rédaction plus lourde mais plus aisée pour les calculs effectifs. L'espace F est de dimension m. Si (f1, … , fm) est une base de F, la fonction ψ peut aussi être vue comme m fonctions de n variables :

ou encore

L'ensemble G peut être vu comme une unique contrainte exprimée par une fonction à valeurs dans F ou encore comme m contraintes exprimées par les égalités ψj(x) = 0, à valeurs réelles.

Un corollaire du
théorème de Rolle indique que l'optimum est atteint en un point de différentielle nulle.
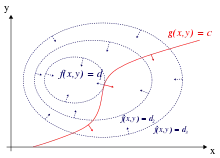
Le fondement théorique de la méthode du multiplicateur de Lagrange peut être vu comme analogue au
théorème de Rolle.
Les fonctions φ et ψ sont de classe C1, ce qui signifie qu'elles sont différentiables, autrement dit elles admettent chacune une application linéaire tangente en chaque point. Le terme C1 signifie aussi que les applications qui, à un point associent les différentielles, soit de φ soit de ψ, sont continues.
L'optimum recherché vérifie une propriété analogue à celle du théorème de Rolle. Un corollaire de ce théorème, illustré à gauche, indique que l'optimum, un maximum ou un minimum, s'il se situe dans l'intervalle ouvert ]a, b[, possède une tangente horizontale, ce qui signifie encore que sa différentielle est nulle. C'est un résultat de cette nature qui est recherché. On peut le visualiser sur la figure de droite, si n et m sont respectivement égaux à 2 et à 1. On représente φ (noté f sur la figure de droite) en bleu par ses courbes de niveau, comme les géographes. Les flèches représentent le gradient de la fonction φ. La différentielle de φ en un point est une application linéaire de E dans ℝ, c'est-à-dire une forme duale. Il est d'usage de considérer E comme un espace euclidien, de choisir la base de E orthonormale et d'identifier la différentielle avec le vecteur de E qui représente la forme duale. Dans ce cas, l'approximation linéaire tangente s'écrit :

La lettre o désigne un petit o selon la notation de Landau et le point entre le gradient de φ et h symbolise le produit scalaire. Le vecteur gradient est orthogonal à la courbe de niveau, dans le sens des valeurs croissantes de φ et de norme proportionnelle à la vitesse d'accroissement de φ dans cette direction. La contrainte vérifie une propriété analogue puisqu'elle est aussi différentiable. L'ensemble étudié est celui des valeurs x telles que ψ(x) est nul. Si x0 est élément de G, les points voisins de x0 dans G ont aussi une image nulle par ψ, autrement dit, l'espace tangent à G au point x0 est formé par les accroissements h de x0 qui ont une image nulle par la différentielle de ψ. La direction de l'espace tangent est le noyau de l'application différentielle de ψ. Une analyse par les fonctions coordonnées ψi exprime ce résultat en indiquant que l'espace tangent est l'intersection des hyperplans orthogonaux des gradients des ψi.
Une analyse au point optimal x0 recherché indique, en approximation du premier ordre, qu'un déplacement h dans la direction de l'espace tangent à G ne peut pas accroître la valeur de φ. Ceci signifie que le déplacement h est nécessairement orthogonal au gradient de φ en x0. C'est ainsi que se traduit le théorème de Rolle, dans ce contexte. Géométriquement, cela signifie que la courbe de niveau bleue et la ligne rouge sont tangentes au point recherché. Analytiquement cela se traduit par le fait que le noyau de la différentielle de ψ en x0 est orthogonal au gradient de φ en ce point.
Une approche intuitive du théorème
Il est peut-être utile, à ce stade, de fournir une approche intuitive du théorème, en se donnant un exemple ayant valeur générale. Considérons donc comme précédemment une fonction différentiable φ(x, y, z) de ℝ3 dans ℝ , dont on se propose de trouver les extrema sous l'unique contrainte ψ(x,y,z) = 0, avec ψ: ℝ3 → ℝ différentiable.
On verra ensuite comment s'y prendre pour deux contraintes.
Rappelons d'abord que la différentielle de φ en un point M de l'espace s'écrit
 ,
,
soit en notant φ' le vecteur


L'interprétation bien connue de ces relations est qu'un déplacement infinitésimal
de vecteur dM au point M induit une variation infinitésimale de la fonction φ, égale au produit scalaire de
φ' (appelé vecteur gradient de φ) avec dM.
Considérons maintenant la contrainte ψ(x,y,z) = 0, qui définit une surface S dans l'espace, tout au moins localement[5].
Il est clair que le problème revient à trouver les points extremum de la restriction de φ à S.
La différentielle de ψ en un point M de l'espace s'écrit, comme précédemment,

Cette relation est en particulier vraie si le point M est sur S.
Mais supposons de plus qu'on astreigne le déplacement infinitésimal dM
à s'effectuer sur S ; alors puisque ψ est identiquement nulle sur S, il en est
de même de sa variation infinitésimale sur S, et dM devra donc vérifier la relation

Vu que dM est quelconque sur S, cela signifie que ψ'(M) est orthogonal à S au point M.
Maintenant, si la restriction de φ à S est extrémale au point M (ce que l'on cherche), alors pour tout déplacement infinitésimal dM en M s'effectuant sur S, la variation infinitésimale correspondante de φ devra être nulle: on peut se contenter de ressentir ce fait, ou bien de s'appuyer sur l'homologie avec les fonctions d'une seule variable réelle, ou encore de le justifier formellement en considérant des courbes paramétrées sur S passant par
M et de vecteur dérivé en M proportionnel à dM[6].
Mathématiquement, cela signifie que

Ainsi, φ'(M) doit être orthogonal à dM, tout comme l'est ψ'(M) d'après ce qu'on a vu plus
haut. Il revient au même de dire que φ'(M) est colinéaire à ψ'(M)[7], ou bien

On peut écrire cette relation sous la forme

Cette équation, alliée avec l'équation de contrainte originale ψ(M) = 0,
constitue la méthode des multiplicateurs de Lagrange.
Dans le cas de deux contraintes ψ1(M) = 0 et ψ2(M) = 0,
on a une intersection de deux surfaces de contraintes, c'est-à-dire une courbe 𝒞 en général.
Le problème revient cette fois à chercher les extrema de la restriction de φ à 𝒞.
Le même raisonnement que précédemment s'applique, mais dM sera cette fois astreint à appartenir à 𝒞, c'est-à-dire à être orthogonal au sous-espace T engendré par les vecteurs ψ'1(M) et ψ'2(M).
Donc les points extremum seront les points M tels que φ'(M) ∈ T, ou bien

Comme précédemment, la méthode des multiplicateurs de Lagrange s'ensuit immédiatement.
Le même raisonnement s'applique dans les espaces euclidiens de dimension n > 3,
ou la fonction objectif est soumise à au plus n–1 équations de contraintes à n variables:
il suffit de remplacer la notion de "surface" par celle d'"hyperplan".
Théorèmes
Le problème à résoudre est de trouver le minimum suivant :

Les fonctions φ et ψ ne sont pas nécessairement définies sur tout E mais au moins sur des ouverts de E, où elles sont supposées différentiables, avec Dψ(x0) surjective[8].
Théorème des extrema liés —
Si le point x0 est un extremum local de φ dans l'ensemble G, alors le noyau de la différentielle de ψ au point x0 est orthogonal au gradient de φ en ce point.
Plus simplement : au point x0, le noyau de Dψ(x0) est inclus dans celui de Dφ(x0), c'est-à-dire, d'après les propriétés des formes linéaires : Dφ(x0) est une combinaison linéaire de Dψ1(x0), … , Dψm(x0), où les ψj sont les composantes de ψ dans une base de F (voir supra). Autrement dit[2] - [3] :
 .
.
Cette formulation plus simple[9] met en évidence le multiplicateur. Si l'on souhaite la réécrire en termes de gradients, il est nécessaire d'équiper F du produit scalaire tel que sa base soit orthonormale, le symbole t signifie la transposée d'une application linéaire ; elle définit une application du dual de F, ici identifié à F dans le dual de E, encore identifié à E :
Corollaire 1 —
Si le point x0 est un extremum local de φ dans l'ensemble G et si la différentielle de ψ au point x0 est surjective, il existe un vecteur λ0 de F tel que :
 .
.
Sous forme de coordonnées, on obtient :

Un deuxième corollaire est plus pragmatique, car il offre une méthode effective pour déterminer l'extremum. Il correspond à la méthode utilisée dans l'exemple introductif.
Corollaire 2 —
Si le point x0 est un extremum local de φ dans l'ensemble G et si la différentielle de ψ au point x0 est surjective, alors il existe un vecteur λ0 de F tel que la fonction L de E×F dans ℝ admet un gradient nul en (x0, λ0)[10] :

Ces théorèmes possèdent quelques faiblesses, de même nature que celle du théorème de Rolle. La condition est nécessaire, mais pas suffisante. Un point de dérivée nulle pour Rolle ou vérifiant les hypothèses du théorème du multiplicateur de Lagrange n'est pas nécessairement un maximum ou un minimum. Ensuite, même si ce point est un extremum, il n'est que local. Si une solution x0 est trouvée, rien n'indique que cet extremum local est le meilleur. L'approximation linéaire ne précise pas si cet optimum est un maximum ou un minimum. Enfin, comme pour le cas du théorème de Rolle, si les domaines de définition ne sont pas ouverts, il est possible qu'un point frontière soit un optimum qui ne vérifie pas le théorème. Ainsi, sur la figure de gauche, f(a) et f(b) sont des minima mais la dérivée n'est nulle ni en a, ni en b.
Il existe deux méthodes célèbres pour démontrer les résultats de Lagrange. La première est souvent appelée méthode des pénalités[12], elle consiste à considérer une suite (χk) définie de la manière suivante :

La suite des minima de ces fonctions tend vers x0.
L'autre méthode[13] utilise le théorème des fonctions implicites.
C'est un dérivé de cette méthode qui est utilisé ici. Le théorème n'est pas utilisé, mais les inégalités à la base de la démonstration sont présentes dans la preuve.
- Cas où ψ est une fonction affine :
La démonstration de ce cas particulier n'est pas nécessaire pour le cas général, en revanche, elle permet de comprendre la logique utilisée et fixe les notations. Soit x1 un point de E tel que la différentielle de ψ possède un noyau qui n'est pas dans l'orthogonal du gradient de φ. On montre que x1 n'est pas un extremum. La contraposée de ce résultat permet de conclure.
Par hypothèse, il existe un vecteur k1 élément du noyau de la différentielle de ψ au point x1 (qui est d'ailleurs la même en chaque point car ψ est une application affine) et qui n'est pas orthogonal au gradient. On choisit k1 de norme 1 et de sens tel que le produit scalaire de ce vecteur avec le gradient soit strictement positif. On note α ce produit scalaire. Si s est un réel positif, l'égalité définissant le gradient, appliquée au vecteur sk1 est

Si s est choisi suffisamment petit, alors o(s) peut être choisi plus petit, en valeur absolue, que n'importe quelle constante strictement positive que multiplie s, par exemple : sα/2. De manière formelle :
![\exists \mu >0,\;\forall s\in ]0,\mu [\quad \varphi (x_{1}+sk_{1})\geq \varphi (x_{1})+s\alpha -{\frac {s\alpha }{2}}=\varphi (x_{1})+{\frac {s\alpha }{2}}.](https://img.franco.wiki/i/b951ca6becd482f6a98e250e072b26644afe5351.svg)
Le fait que l'image par ψ de x1 + sk1 soit un élément de G, ainsi que la majoration précédente, montrent que x1 ne peut être un maximum local. En choisissant s négatif, on montre que x1 ne peut pas non plus être un minimum local.
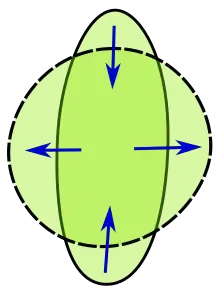
Dans le cas général, on ne peut supposer que x1 + sk1 soit élément de G. La situation est illustrée sur la figure de droite. L'ensemble G est représenté en bleu, le gradient de φ en rouge et la droite dirigée par k1 en vert. Pour une valeur de s suffisamment petite, on construit un vecteur k, égal à sk1 et proche de G. Une technique analogue à celle du théorème des fonctions implicites permet de trouver un point x2, suffisamment proche de x1 + k pour que le raisonnement précédent puisse s'appliquer avec peu de modifications. La technique consiste à établir quatre inégalités qui montrent le résultat recherché.
- Première inégalité :
- Elle consiste à utiliser la définition du gradient au point x1 mais, cette fois-ci, valable pour tout vecteur de norme suffisamment petite :

Par rapport au cas particulier affine, la constante est choisie un peu différemment, elle est maintenant égale à α/8. La zone sur laquelle la majoration est vérifiée est un peu modifiée, elle correspond maintenant aux vecteurs de normes plus petites que 2μ1. Les raisons techniques qui poussent à ces modifications apparaissent à la conclusion de cette démonstration.
- Deuxième inégalité :
- La deuxième inégalité permet de borner la norme du vecteur, illustré en bleu ciel et qu'il faut ajouter à x1 + sk1 pour retrouver le point de G qui montre que x1 n'est pas un maximum local. L'objectif est de montrer qu'il existe un réel strictement positif m tel que

- Ici, le symbole Bx1 désigne la boule de centre x1 et de rayon 1. Pour établir ce résultat, on utilise deux propriétés des compacts. Une fonction continue l'est uniformément sur un compact, ensuite elle atteint sa borne inférieure. La différentielle de ψ en un point quelconque est continue, comme d'ailleurs toute application linéaire en dimension finie. Composée avec la norme, aussi continue, elle atteint sa borne inférieure sur l'intersection de l'orthogonal de son noyau et de la sphère unité. Cette intersection est en effet compacte. On appelle f la fonction qui à une application linéaire de E dans F associe cette borne inférieure. Par construction elle ne peut prendre de valeur nulle. On considère ensuite la fonction g, qui à x élément de E associe l'image par f de la différentielle de ψ au point x. Une fois sa continuité sur la boule fermée de centre x1 et de rayon 1 démontrée, on sait que cette fonction atteint son minimum m. La majoration (2) définit ce minimum.
- Pour établir l'inégalité (2), il suffit donc démontrer la continuité de g. L'application qui à x associe la différentielle de ψ au point x est continue par hypothèse. Elle est donc uniformément continue sur la boule de centre x1 et de rayon 1 :

- Soit v1 (resp. v2) un vecteur unitaire tel que

- L'espace des applications linéaires de E dans F est muni de la norme qui associe à une application la borne supérieure des normes de son image de la boule unité. Comme les points y1 et y2 sont choisis à une distance inférieure à
 l'un de l'autre, on dispose de la majoration
l'un de l'autre, on dispose de la majoration

- Cette majoration, ainsi que la même appliquée à y2, démontre la continuité recherchée pour conclure la preuve de la majoration (2) :

- Troisième inégalité :
- On dispose d'une majoration comparable à (1), mais cette fois appliquée à ψ et utilisant la continuité uniforme. Il existe un réel strictement positif μ2 tel que, si θ désigne l'angle entre le gradient de φ au point x1 et k1 :

- Quatrième inégalité :
- La fonction Dψ, qui au point x associe la différentielle de ψ au point x est continue, en particulier au point x1, ce qui montre que

Une fois les quatre inégalités établies, il devient possible de définir les vecteurs h et k et de conclure. Soit s un réel strictement strictement positif et plus petit que μ1, μ2, μ3 et que 1/2, on définit le vecteur k de la figure comme étant égal à sk1. Soit x2 le vecteur le plus proche de x + k et élément de G et h le vecteur x2 – x1. Enfin, l1 désigne le vecteur unitaire colinéaire à h – k et de même sens ; c'est le vecteur illustré en bleu ciel sur la figure. Le réel positif t est tel que tl1 soit égal à h – k. Le choix du vecteur k est tel que t est suffisamment petit pour conclure.
- Conclusion :
- Le point tl1 est le plus petit vecteur de E tel que x1 + sk1 + tl1 est un élément de G. Autrement dit :

- La majoration (3), appliquée au point x2, se traduit par :

- De plus, par définition de k1, la différentielle en x1 de ψ est nulle sur k1. On en déduit, d'après la majoration (4) :

- Le point tl1 est le plus petit vecteur de E tel que x1 + sk1 + tl1 est un élément de G. On remarque que x1 est un élément de G. En conséquence, x1 + sk1 est aussi un élément de G et tl1 est de norme plus petite que sk1, ce qui revient à dire que t est plus petit que s, donc :

- Le vecteur l1 est orthogonal au noyau de Dψ au point x2. En effet, le point x2 est le plus proche de x2 – tl1 dans G. Si p est un vecteur du noyau, x2 + up est plus loin de x2 – tl1 que ne l'est x2 ; ici, u désigne un nombre réel :

- ce qui montre que
![\exists \epsilon >0,\;\forall u\in ]-\epsilon ,\epsilon [\quad u(tl_{1}\cdot p+u\|p\|^{2})\geq 0.](https://img.franco.wiki/i/3e50d2ba4276abbd1c514e2f67af95eed52be5a9.svg)
- Le produit scalaire de l1 et p est nul, ce qui montre bien que l1 est orthogonal au noyau de Dψ au point x2. Le point x2 est élément de la boule de rayon 1 et centre x1. La majoration (2) montre que

- On peut maintenant appliquer la majoration (1) :

- et

Le point x2 est un élément de G ayant une image par φ strictement plus grande que x1, ce qui montre que x1 n'est pas un maximum local. On montre de même que x1 n'est pas non plus un minimum local, ce qui termine la démonstration.
- Il existe un vecteur λ0 de F tel que la somme de l'image de λ0 par la transposée de la différentielle de ψ au point x0 et du gradient de φ en ce point soit nulle :

C'est une conséquence directe du résultat précédent et des propriétés de la transposition. Remarquons tout d'abord que l'image de la transposée d'une application linéaire est un sous-espace vectoriel inclus dans l'orthogonal du noyau. Pour s'en convaincre, montrons qu'un élément v de l'image de la transposée de la différentielle de ψ au point x0, d'antécédent λ, est orthogonal à tout élément w du noyau de la différentielle :

Montrons maintenant que l'orthogonal du noyau de la différentielle possède la même dimension que l'image de la transposée. L'application différentielle est surjective, son image est de dimension m, la transposée ne modifie pas le rang d'une application linéaire, l'image de sa transposée est donc aussi de dimension m. La somme des dimensions de l'image et du noyau est égale à celle de l'espace vectoriel de départ, ici E de dimension n. Comme l'image est de dimension m, le noyau est de dimension n - m. L'orthogonal du noyau est donc de dimension m. Pour résumer, l'orthogonal du noyau de la différentielle contient l'image de sa transposée et est de même dimension, ce qui montre l'égalité des deux sous-espaces vectoriels. Le gradient de φ au point x0 est dans l'orthogonal au noyau de la différentielle, il est donc dans l'image de sa transposée, ce qui montre l'existence du vecteur λ0.
- Il existe un vecteur λ0 de F tel que la fonction L de E×F dans ℝ admet un gradient nul en (x0, λ0) :

Pour cela, calculons l'image de (u, μ), un point de E×F par la différentielle de L au point (x0, λ0), λ0 étant le vecteur de F défini lors de la démonstration précédente.

La définition de λ0 montre que

Le gradient recherché est bien nul au point étudié.
Écriture du problème
Si l'écriture condensée permet de mieux comprendre la structure du théorème, les notations développées sont plus utiles pour une résolution effective. Dans la pratique, on considère souvent une fonction φ de ℝn dans ℝ et m fonctions ψj, avec j variant de 1 à m, aussi de ℝn dans ℝ. L'entier m est nécessairement plus petit que n pour pouvoir appliquer les théorèmes du paragraphe précédent. On cherche à trouver un n-uplet (a1, … , an) tel que
![(1)\quad \varphi (a_{1},\cdots ,a_{n})=\min _{(x_{i})\in G}\varphi (x_{1},\cdots ,x_{n})\quad {\text{avec}}\quad G=\{(x_{i})\in \mathbb {R} ^{n}\mid \forall j\in [1,m]\;\psi _{j}(x_{1},\cdots ,x_{n})=0\}.](https://img.franco.wiki/i/f36a494a462eac9987fec2dfdb99d7fba9bf7572.svg)
Pour cela, on définit la fonction L de ℝn+m dans ℝ par :

Le deuxième corollaire indique une condition nécessaire pour élucider le problème d'optimisation (1). Le n-uplet (a1, … , an) est une solution de (1) seulement s'il existe un m-uplet (α1, … , αm) tel que le (n + m)-uplet (a1, … , an, α1, … , αm) soit solution des n + m équations :
![{\displaystyle \forall i\in [\![1,n]\!]\quad {\frac {\partial \varphi }{\partial x_{i}}}(x_{1},\cdots ,x_{n})+\sum _{j=1}^{m}\lambda _{j}{\frac {\partial \psi _{j}}{\partial x_{i}}}(x_{1},\cdots ,x_{n})=0\quad {\text{et}}\quad \forall j\in [\![1,m]\!]\quad \psi _{j}(x_{1},\cdots ,x_{n})=0.}](https://img.franco.wiki/i/4d4856212beb15693ae5288bdc7ca6b17cd89c34.svg)
Cette méthode peut être généralisée aux problèmes d'optimisation incluant des contraintes d'inégalités (ou non linéaires) en utilisant les conditions de Kuhn-Tucker.
Mais également sur des fonctions discrètes à maximiser ou minimiser sous contraintes, moyennant un changement d'interprétation, en utilisant la méthode des multiplicateurs d'Everett (ou de Lagrange généralisés), plus volontiers appelée méthode des pénalités.
Application : inégalité arithmético-géométrique
La méthode du multiplicateur de Lagrange permet de démontrer l'inégalité arithmético-géométrique[14]. On définit les applications φ et ψ de ℝ+n dans ℝ par :

On remarque que l'ensemble G, composé des n-uplets de coordonnées positives et de somme égale à s est un compact de ℝn. Sur ce compact la fonction φ est continue, et donc elle admet nécessairement un maximum. Les deux fonctions φ et ψ sont bien de classe C1, il est donc possible d'utiliser le multiplicateur de Lagrange pour trouver ce maximum. Pour cela, on considère la fonction L :

Une solution vérifie les équations :
![{\displaystyle \forall i\in [\![1,n]\!]\quad {\frac {\partial L}{\partial x_{i}}}(x_{1},\cdots x_{n},\lambda )=0\Leftrightarrow \prod _{k\neq i}x_{k}=-\lambda \quad {\text{et}}\quad \sum _{i=1}^{n}x_{i}=s.}](https://img.franco.wiki/i/ae23101e55f4dc8dca46919abefa74b81663397d.svg)
On en déduit l'existence d'une unique solution, obtenue pour tous les xi égaux à s/n = x et λ égal à –(s/n)n–1, ce qui s'exprime, en remplaçant s par sa valeur :
![\forall (x_{i})\in \mathbb {R} _{+}^{n}\quad {\sqrt[{n}]{\prod _{i=1}^{n}x_{i}}}\leq {\frac {\sum _{i=1}^{n}x_{i}}{n}}.](https://img.franco.wiki/i/0177c94213a50245505d5f9ae3ba33ee56871fd6.svg)
La moyenne géométrique est inférieure à la moyenne arithmétique, l'égalité n'ayant lieu que si les xi sont tous égaux.
Le multiplicateur de Lagrange offre une démonstration alternative de l'inégalité arithmético-géométrique.
Espace fonctionnel
La méthode se généralise aux espaces fonctionnels. Un exemple est donné par la question de la chaînette, qui revient à rechercher la position que prend, au repos, une chaînette attachée à ses deux extrémités. L'optimisation correspond à la position offrant un potentiel minimal, la contrainte est donnée par la position des extrémités et la longueur de la chaînette, supposée fixe. Cette méthode permet de trouver des plus courts chemins sous contrainte, ou encore des géodésiques. Le principe de Fermat ou celui de moindre action permet de résoudre de nombreuses questions à l'aide de cette méthode.
Exemple introductif : la chaînette
Considérons donc une chaînette soumise à la gravité et recherchons son équilibre statique. La chaînette est de longueur a et l'on suppose qu'elle est accrochée à deux points d'abscisses –t0 et t0 et d'ordonnée nulle en ces deux points. Si son ordonnée est notée x, elle suit une courbe y = x(t) sur l'intervalle [–t0, t0], dont on se propose de calculer l'équation.
Dire qu'elle est à l'équilibre revient à dire que son potentiel Φ est minimal, où :

Ici, α désigne une constante physique, en l'occurrence le produit de la gravitation terrestre g par la masse linéique de la chaînette, supposée constante. La formule donnant la longueur d'un arc en fonction d'un paramétrage est donnée dans l'article Longueur d'un arc.
La chaînette n'est pas supposée être élastique, elle vérifie donc la contrainte Ψ, indiquant que sa longueur l0 n'est pas modifiée :

Si C1K(I) désigne l'ensemble des fonctions de [–t0, t0] dans ℝ, dérivables et de dérivées continues, nulles en –t0 et t0, le problème revient à rechercher la fonction x0 telle que

La similitude avec la situation précédente est flagrante. Pour pouvoir appliquer des multiplicateurs de Lagrange, il faut donner un sens aux gradients de Φ et Ψ. Dans le cas où il existe deux fonctions de classe C2 de ℝ3 dans ℝ, notées φ et ψ, telles que

L'équation d'Euler-Lagrange affirme que

Dans le cas particulier où les fonctions φ et ψ sont des fonctions de deux variables et ne dépendent pas de t, on obtient la formulation de Beltrami (cf. l'article « Équation d'Euler-Lagrange ») :

Dire que les deux gradients sont colinéaires revient à dire qu'il existe un réel λ, le multiplicateur de Lagrange, tel que

La résolution de cette équation différentielle est une chaînette. La méthode du multiplicateur de Lagrange permet bien de résoudre la question posée[15].
Everett : cas des fonctions non continues, non dérivables
Hugh Everett généralise la méthode aux fonctions non dérivables, souvent choisies convexes. Pour une résolution effective, il devient nécessaire de disposer d'un algorithme déterminant l'optimum (ou les optima) d'une fonction. Dans le cas non dérivable, on peut utiliser une heuristique adéquate ou encore une méthode de Monte-Carlo.
Il faut ensuite réviser pour l'itération suivante les multiplicateurs (ou « pénalités ») de façon appropriée, et c'est là que se situe l'apport essentiel d'Everett : il mémorise les jeux de multiplicateurs utilisées lors des deux dernières itérations, et sépare en trois les résultats pour chaque contrainte. Selon que sur les deux dernières itérations il y a eu rapprochement de l'objectif, ou encadrement, ou encore éloignement (à cause de l'effet des autres multiplicateurs), chaque multiplicateur est ajusté pour l'itération suivante d'une façon qui garantit la convergence si une relation entre les trois ajustements, qu'il fournit, est observée.
Espace de Sobolev
L'exemple précédent montre que le contexte de l'équation d'Euler-Lagrange n'est pas loin de celui du multiplicateur de Lagrange. Si l'ensemble de départ de la fonction x(t) recherchée est un intervalle réel I ouvert et borné et l'ensemble d'arrivée E l'espace vectoriel euclidien, la généralisation est relativement aisée.
On suppose l'existence d'une fonction Φ à minimiser, son ensemble de départ est un espace fonctionnel, c'est-à-dire un espace vectoriel de fonctions, de I dans E et son ensemble d'arrivée ℝ. La fonction Φ est construite de la manière suivante :

Le point sur le x indique la fonction gradient, qui à t associe le gradient de x au point t.
La fonction φ est une fonction de ℝ×E2 dans ℝ de classe C2. L'optimisation est sous contrainte, donnée sous une forme analogue à la précédente. On suppose l'existence d'une fonction Ψ de ℝ×E2 dans F, un espace euclidien. La fonction Ψ est encore définie à l'aide d'une fonction ψ de classe C2 de I×E2, mais cette fois dans un espace euclidien F :

L'ensemble G est composé de fonctions deux fois dérivables de I dans E et dont l'image par Ψ est nulle. On suppose de plus que les valeurs des fonctions de G aux bornes de I sont fixes et, quitte à opérer une translation, on peut toujours supposer, sans perte de généralité, que ces fonctions sont nulles aux bornes de I.
La seule tâche un peu délicate est de définir l'espace vectoriel W2,2(I, E) sur lequel opèrent Φ et Ψ. Pour définir un équivalent de gradient, cet espace comporte nécessairement un produit scalaire. Si l'on souhaite établir des théorèmes équivalents aux précédents, les fonctions dérivée et dérivée seconde sont définies et l'espace est complet. Un espace muni d'un produit scalaire et complet est un Hilbert. Sa géométrie est, de fait, suffisamment riche pour étendre les résultats précédents.
On note D l'espace des fonctions de I, à valeur dans E, de classe C∞ et à support compact et D* son dual topologique. L'espace D est muni de la norme de la borne supérieure et l'espace D* est celui des distributions. Ce premier couple n'est pas encore satisfaisant car D est « trop petit » et D* « trop gros » pour permettre de définir un bon produit scalaire, à l'origine d'une géométrie aussi simple que celle d'un Hilbert.
L'espace D* contient l'espace de Hilbert L2(I, E) des fonctions de carré intégrable. En effet une fonction f de L2(I, E) agit sur D par le produit scalaire 〈∙, ∙〉L défini par l'intégrale de Lebesgue :

C'est dans L2(I, E) que nous cherchons le bon espace. Dans cet espace, l'intégration par parties permet de définir la dérivée de la fonction f de L2(I). Comme g est à support compact et que I est ouvert, aux bornes de I, la fonction g est nulle. Si f est dérivable au sens classique du terme, on bénéficie des égalités :
![\langle {\dot {f}},g\rangle _{L}=\int _{I}{\dot {f}}(t)\cdot g(t)\mathrm {d} t={\Big [}f(t)\cdot g(t){\Big ]}_{I}-\int _{I}f(t)\cdot {\dot {g}}(t)\mathrm {d} t=-\int _{I}f(t)\cdot {\dot {g}}(t)\mathrm {d} t.](https://img.franco.wiki/i/c501bf752d49ba7e46bc68393aab7737ab4f8d4f.svg)
Si la distribution dérivée de f est encore d'un élément de L2(I, E), on dit qu'elle est dérivable au sens de Sobolev. Si cette dérivée est encore dérivable au sens précédent, on dit qu'elle est deux fois dérivable au sens de Sobolev. On note W2,2(I, E) le sous-espace de L2(I, E) équipé du produit scalaire 〈∙, ∙〉W suivant :

Les intégrales sont bien définies car elles correspondent au produit de deux éléments de L2(I, E). Il est ensuite simple de vérifier que l'espace est bien complet[16]. Enfin, si f est une fonction dérivable au sens des distributions, il existe un représentant continu de f[17]. Ainsi, tout élément de W2,2(I, E) admet un représentant continu et dont la dérivée admet aussi un représentant continu.
Équation d'Euler-Lagrange
La difficulté est maintenant d'exprimer le gradient des fonctions Φ et Ψ. L'équation d'Euler-Lagrange cherche dans un premier temps à trouver des fonctions de classe C2 qui minimisent Φ. L'espace vectoriel sous-jacent est celui des fonctions d'un intervalle borné et de classe C2 et nulles aux bornes de l'intervalle. Sur cet espace, le calcul du gradient de Φ n'est guère complexe, il donne aussi une idée de la solution ainsi que de la méthode pour y parvenir. En revanche, ce calcul est insuffisant dans le cas présent. Avec le « bon » produit scalaire, l'espace des fonctions de classe C2 n'est pas complet, ce qui empêche de disposer de la bonne géométrie permettant de démontrer la méthode du multiplicateur de Lagrange.
L'objectif est de généraliser un peu la démonstration pour permettre de disposer de l'égalité du gradient dans l'espace complet W2,2(I, E). Dans un premier temps, exprimons l'égalité qui définit la différentielle de Φ en un point x, qui représente une fonction de W2,2(I, E) :

L'application DΦx est une application linéaire continue de W2,2(I, E) dans ℝ, c'est-à-dire un élément du dual topologique de W2,2(I, E), que le produit scalaire permet d'identifier à W2,2(I, E). L'égalité précédente devient :

Autrement dit, le gradient de Φ au point x est une fonction de L2(I, E) dans ℝ. De fait, ce gradient s'exprime à l'aide de l'équation d'Euler-Lagrange :
Le gradient de Φ au point x est la fonction de I dans E, définie par

Si la fonction φ est en général choisie au sens usuel de la dérivation, la fonction x(t) est une fonction de W2,2(I, E). Le symbole d/dt doit être pris au sens de la dérivée d'une distribution, qui n'est ici nécessairement une fonction de carré intégrable, définie presque partout.
Pour Ψ, la logique est absolument identique, mais cette fois-ci, la fonction est à valeurs dans F. En conséquence, la dérivée partielle de ψ par rapport à sa deuxième ou troisième variable n'est plus une application linéaire de E dans ℝ mais de E dans F. Ainsi, la différentielle de Ψ au point, une fonction x de I dans E, est une application de I dans l'espace L(E, F) des applications linéaires de E dans F. La logique reste la même.
La différentielle de Ψ au point x est la fonction de I dans L(E, F) définie par

Démonstration
- L'application Φ est différentiable au point x, si x est une fonction de W2,2(I, E) nulle aux bornes de I :
Cette proposition revient à montrer que

Soit ε un réel strictement positif. La fonction x et sa dérivée possède un représentant continu, dont les valeurs aux bornes de l'intervalle I sont nulles. En conséquence l'image de I par x et par sa dérivée est sont des compacts de E. Soit H le produit cartésien de I, x(I) et dx/dt(I). Le produit de trois compacts est encore un compact. La fonction différentielle de φ sur ce compact est uniformément continue. On en déduit que les dérivée partielles à l'ordre 1 sont bornées par une valeur, notée M1 ; on en déduit aussi, si a et b désignent les bornes de I :


De plus, sur le compact H, la valeur absolue de φ et la norme de ses trois dérivées partielles sont majorées par une constante M, car φ est continue. Si la norme de h dans W2,2(I, E) est plus petite que μ2, il existe un ensemble Iμ de I de mesure plus grande que b – a – εμ2/8M sur lequel h et sa dérivée ne dépassent pas μ. La majoration (2) montre que

Sur le complémentaire de Iμ dans I, comme la fonction φ ne dépasse pas M en valeur absolue et comme le complémentaire est de mesure inférieure à εμ2/8M, on obtient :

En sommant les deux dernières majorations, on trouve bien la majoration (1) qui montre la différentiabilité de Φ.
- Le gradient de Φ au point x est donné par l'équation de Lagrange :
Une fois la proposition précédente démontrée, le reste du calcul est le même que celui de l'article Équation d'Euler-Lagrange. Le calcul consiste à exprimer différemment le gradient de Φ au point x :

Le fait que la fonction h soit nulle aux bornes de I et une intégration par parties montrent que
![\int _{I}{\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\cdot {\dot {h}}(t)\mathrm {d} t=\left[{\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\cdot h(t)\right]_{a}^{b}-\int _{I}{\frac {d}{dt}}\left({\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\right)\cdot h(t)\mathrm {d} t=-\int _{I}{\frac {d}{dt}}\left({\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\right)\cdot h(t)\mathrm {d} t,](https://img.franco.wiki/i/31c884478082381f0b25883ba58d1add28faa3d9.svg)
ce qui permet de déduire que

et démontre ainsi la proposition. Les calculs sont exactement les mêmes pour la fonction Ψ.
Théorèmes
Ce paragraphe est très proche du précédent dans le cas de la dimension finie. Le problème à résoudre est de trouver le minimum suivant :

Théorème du multiplicateur de Lagrange —
Si le point x0 est un extremum local de Φ dans l'ensemble G, alors le noyau de la différentielle de Ψ au point x0 est orthogonal au gradient de Φ en ce point.
On obtient les mêmes corollaires, que l'on peut écrire :
Corollaire —
Si le point x0 est un extremum local de Φ dans l'ensemble G et si la différentielle de Ψ au point x0 est surjective, alors il existe un vecteur λ0 de F tel que la fonction L de W2,2(I, E)×F dans ℝ admet un gradient nul en (x0, λ0) :

Cette équation s'écrit encore :

Le signe d/dt doit être pris au sens de la dérivée des distributions. On obtient une solution faible, c'est-à-dire une fonction x définie presque partout et dérivable dans un sens faible. En revanche, si une fonction x de classe C2 est solution du problème de minimisation, comme ses dérivées premières et secondes sont des représentants de ses dérivées au sens faible, l'équation précédente est encore vérifiée.
Démonstrations
La démonstration est proche de la précédente, néanmoins elle doit être adaptée au passage d'un espace euclidien à un hilbertien :
- Cas où Ψ est une fonction affine :
La démonstration précédente n'utilise pas la dimension finie. Elle s'applique donc encore de la même manière.
Une partie peut être reprise intégralement.
- Première inégalité :
- Elle consiste à utiliser la définition du gradient au point x1 mais, cette fois-ci, valable pour tout vecteur de norme suffisamment petite, qui n'utilise pas la dimension finie :

- Deuxième inégalité :
- La deuxième inégalité est démontrée, dans la démonstration précédente, à l'aide de la dimension finie. Ici, on restreint nos ambitions pour uniquement montrer l'existence de deux nombres réels strictement positifs m et r tels que

La démonstration reste néanmoins un peu analogue. Soit x un point de la boule de centre x1 et de rayon 1. L'image de la différentielle de Ψ au point x et un espace vectoriel de dimension finie, le noyau est de codimension finie et son orthogonal de dimension finie. L'intersection de cet orthogonal avec la sphère unité est un compact, ce qui permet de définir les fonctions f et g comme pour le cas de la dimension finie. La continuité de g montre l'implication (2).
L'application qui à tout élément x de W2,2(I, E) associe DΨx est continue par hypothèse, ce qui se traduit par :

Soit v1 (resp. v) un point de l'intersection de la sphère unité et de l'orthogonal du noyau de DΨ au point x1 (resp. x), tel que

La continuité de la différentielle montre :

Les mêmes majorations montrent que

Ce qui montre la continuité de g et par voie de conséquence la majoration (2) : il suffit de choisir m comme l'inverse de la valeur g(x1).
- Troisième et quatrième inégalités :
La troisième inégalité ne fait pas appel à la dimension finie. On la rappelle dans le nouveau contexte :

Il en est de même pour la quatrième inégalité :

- Conclusion :
La conclusion est la même : il suffit maintenant de choisir μ non seulement plus petit que μ1, μ2 et μ3 mais aussi plus petit que r.
Application : Théorème isopérimétrique
On recherche la surface de plus grande aire, ayant une frontière de longueur égale à 2π. On remarque que la surface est nécessairement convexe, d'intérieur non vide. On considère une droite coupant la surface en deux. Cette droite est utilisée comme axe d'un repère orthonormal, dont les abscisses sont notées par la lettre t et les ordonnées par x. La frontière supérieure est paramétrable en une courbe x(t) et, si le repère est bien choisi, on peut prendre comme abscisse minimale –a et maximale a. On recherche alors une courbe x, définie entre –a et a tel que l'aire A soit maximale :

On sait de plus que la demi-longueur de la frontière est égale à π :

La recherche de la surface se traite aussi avec le multiplicateur de Lagrange. La même astuce que celle utilisée dans l'exemple introductif montre, avec les notations usuelles :

On en déduit l'existence de valeurs λ et k telles que

En notant u = x – k, on obtient :

On trouve l'équation d'un demi-cercle de rayon λ ; la valeur λ est égale à 1 et k à 0[18].

















![{\displaystyle \varphi (x,y,z)={\frac {1}{4}}\left[(x^{2}+y^{2}+z^{2})^{2}-2(x^{4}+y^{4}+z^{4})\right]\quad {\text{et}}\quad \psi (x,y,z)=x+y+z-p.}](https://img.franco.wiki/i/7114803a3fc47a8b9b8be8f9e780c3ab8d697cdd.svg)























![\exists \mu >0,\;\forall s\in ]0,\mu [\quad \varphi (x_{1}+sk_{1})\geq \varphi (x_{1})+s\alpha -{\frac {s\alpha }{2}}=\varphi (x_{1})+{\frac {s\alpha }{2}}.](https://img.franco.wiki/i/b951ca6becd482f6a98e250e072b26644afe5351.svg)
.jpg.webp)














![\exists \epsilon >0,\;\forall u\in ]-\epsilon ,\epsilon [\quad u(tl_{1}\cdot p+u\|p\|^{2})\geq 0.](https://img.franco.wiki/i/3e50d2ba4276abbd1c514e2f67af95eed52be5a9.svg)








![(1)\quad \varphi (a_{1},\cdots ,a_{n})=\min _{(x_{i})\in G}\varphi (x_{1},\cdots ,x_{n})\quad {\text{avec}}\quad G=\{(x_{i})\in \mathbb {R} ^{n}\mid \forall j\in [1,m]\;\psi _{j}(x_{1},\cdots ,x_{n})=0\}.](https://img.franco.wiki/i/f36a494a462eac9987fec2dfdb99d7fba9bf7572.svg)

![{\displaystyle \forall i\in [\![1,n]\!]\quad {\frac {\partial \varphi }{\partial x_{i}}}(x_{1},\cdots ,x_{n})+\sum _{j=1}^{m}\lambda _{j}{\frac {\partial \psi _{j}}{\partial x_{i}}}(x_{1},\cdots ,x_{n})=0\quad {\text{et}}\quad \forall j\in [\![1,m]\!]\quad \psi _{j}(x_{1},\cdots ,x_{n})=0.}](https://img.franco.wiki/i/4d4856212beb15693ae5288bdc7ca6b17cd89c34.svg)


![{\displaystyle \forall i\in [\![1,n]\!]\quad {\frac {\partial L}{\partial x_{i}}}(x_{1},\cdots x_{n},\lambda )=0\Leftrightarrow \prod _{k\neq i}x_{k}=-\lambda \quad {\text{et}}\quad \sum _{i=1}^{n}x_{i}=s.}](https://img.franco.wiki/i/ae23101e55f4dc8dca46919abefa74b81663397d.svg)
![\forall (x_{i})\in \mathbb {R} _{+}^{n}\quad {\sqrt[{n}]{\prod _{i=1}^{n}x_{i}}}\leq {\frac {\sum _{i=1}^{n}x_{i}}{n}}.](https://img.franco.wiki/i/0177c94213a50245505d5f9ae3ba33ee56871fd6.svg)










![\langle {\dot {f}},g\rangle _{L}=\int _{I}{\dot {f}}(t)\cdot g(t)\mathrm {d} t={\Big [}f(t)\cdot g(t){\Big ]}_{I}-\int _{I}f(t)\cdot {\dot {g}}(t)\mathrm {d} t=-\int _{I}f(t)\cdot {\dot {g}}(t)\mathrm {d} t.](https://img.franco.wiki/i/c501bf752d49ba7e46bc68393aab7737ab4f8d4f.svg)











![\int _{I}{\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\cdot {\dot {h}}(t)\mathrm {d} t=\left[{\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\cdot h(t)\right]_{a}^{b}-\int _{I}{\frac {d}{dt}}\left({\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\right)\cdot h(t)\mathrm {d} t=-\int _{I}{\frac {d}{dt}}\left({\frac {\partial \varphi }{\partial {\dot {x}}}}(t)\right)\cdot h(t)\mathrm {d} t,](https://img.franco.wiki/i/31c884478082381f0b25883ba58d1add28faa3d9.svg)
















