Formule de Héron
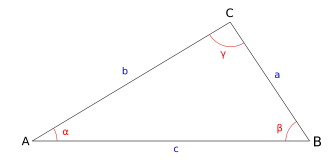
En géométrie euclidienne, la formule de Héron, portant le nom de Héron d'Alexandrie, permet de calculer l'aire S d'un triangle quelconque en ne connaissant que les longueurs a, b et c de ses trois côtés :
La formule était déjà connue d'Archimède[1].
Démonstrations
Héron d'Alexandrie énonce et démontre son théorème dans son traité Les Métriques. Sa démonstration s'appuie sur les propriétés du cercle inscrit dans un triangle et sur l'exploitation des rapports de longueurs dans des triangles semblables[2].
Les propriétés trigonométriques permettent une démonstration plus courte de cette égalité.
Ainsi, la formule de Héron peut se déduire de manière algébrique de la loi des cosinus [3].
Il existe beaucoup d'autres démonstrations : voir notamment l'article « Loi des cotangentes ».
Il existe également un moyen simple de retrouver la formule de Héron par des considérations sur la forme que doit prendre le polynôme S2 en exploitant les propriétés des triangles plats, les propriétés d'homogénéité et de symétrie[4].
Autres écritures de la formule
À l'aide de polynômes symétriques
D'après les calculs intermédiaires ci-dessus, on a aussi :
Sous forme d'un déterminant
On a : (déterminant de Cayley-Menger).
Pour une mise en œuvre numérique
La formule de Héron présente une instabilité lors du calcul numérique, qui se manifeste pour les triangles en épingle, c'est-à-dire dont un côté est de dimension très petite par rapport aux autres (confrontation de petites et grandes valeurs).
En choisissant les noms de côtés de telle sorte que a > b > c, et en réorganisant les termes de façon à optimiser les grandeurs ajoutées ou soustraites, William Kahan propose une formule plus stable[5] :
Généralisations
En géométrie sphérique
En trigonométrie sphérique, il existe une formule analogue à la formule de Héron qui permet de déduire l'aire d'un triangle sphérique à partir de ses côtés : elle est donnée par le théorème de l'Huilier.
Pour les quadrilatères
Il existe des formulations analogues pour déterminer l'aire d'un quadrilatère, mais à moins qu'il soit inscriptible, la donnée supplémentaire d'angles ou des diagonales est nécessaire. Voir : Formule de Bretschneider et Formule de Brahmagupta.
Pour les tétraèdres
Le volume d'un tétraèdre est donné en fonction de la longueur de ses arêtes par le déterminant de Cayley-Menger [6].
Notes et références
- (en) Thomas L. Heath, A History of Greek Mathematics, vol. II, Oxford University Press, , p. 321-323.
- Pour une étude détaillée de sa démonstration voir (en) Christy Williams, Crystal Holcomb et Kayla Gifford, « Héron's Formula for triangular aera », sur Université du Kentucky.
- Mohammed AASSILA, 1000 challenges mathématiques, géométrie, Ellipses, , 25 p., p. 365
- .Exercices de maths -CSK - 2017/2018, Exercice 14, sur le site animath.fr
- (en) W. Kahan, « Miscalculating Area and Angles of a Needle-like Triangle », sur UC Berkeley, .
- Voir aussi « Déterminants de Cayley-Menger », sur mathafou.free.fr.
Voir aussi
Articles connexes
Liens externes
- Michel Hort, « La formule de Héron », sur le-triangle-et-ses-calculs.ch
- (en) Eric W. Weisstein, « Heron's formula », sur MathWorld
- (en) A. Bogomolny, « Heron's Formula », sur Cut The Knot
- (en) [vidéo] Mathologer, Heron’s formula: What is the hidden meaning of 1 + 2 + 3 = 1 x 2 x 3 ? sur YouTube












![{\displaystyle S={\frac {1}{4}}{\sqrt {[a+(b+c)]\,[c-(a-b)]\,[c+(a-b)]\,[a+(b-c)]}}.}](https://img.franco.wiki/i/95db439d696804359fb45ca4d678b874f8250867.svg)