Algorithme du gradient
L'algorithme du gradient, aussi appelé algorithme de descente de gradient, désigne un algorithme d'optimisation différentiable. Il est par conséquent destiné à minimiser une fonction réelle différentiable définie sur un espace euclidien (par exemple, , l'espace des n-uplets de nombres réels, muni d'un produit scalaire) ou, plus généralement, sur un espace hilbertien. L'algorithme est itératif et procède donc par améliorations successives. Au point courant, un déplacement est effectué dans la direction opposée au gradient, de manière à faire décroître la fonction. Le déplacement le long de cette direction est déterminé par la technique numérique connue sous le nom de recherche linéaire. Cette description montre que l'algorithme fait partie de la famille des algorithmes à directions de descente.
Les algorithmes d'optimisation sont généralement écrits pour minimiser une fonction. Si l'on désire maximiser une fonction, il suffira de minimiser son opposée.
Il est important de garder à l'esprit le fait que le gradient, et donc la direction de déplacement, dépend du produit scalaire qui équipe l'espace hilbertien ; l'efficacité de l'algorithme dépend donc de ce produit scalaire.
L'algorithme du gradient est également connu sous le nom d'algorithme de la plus forte pente ou de la plus profonde descente (steepest descent, en anglais) parce que le gradient est la pente de la fonction linéarisée au point courant et est donc, localement, sa plus forte pente (notion qui dépend du produit scalaire).
Dans sa version la plus simple, l'algorithme ne permet de trouver ou d'approcher qu'un point stationnaire (i.e., un point en lequel le gradient de la fonction à minimiser est nul) d'un problème d'optimisation sans contrainte. De tels points sont des minima globaux, si la fonction est convexe. Des extensions sont connues pour les problèmes avec contraintes simples, par exemple des contraintes de borne. Malgré des résultats de convergence théoriques satisfaisants, cet algorithme est généralement lent si le produit scalaire définissant le gradient ne varie pas avec le point courant de manière convenable, c'est-à-dire si l'espace vectoriel n'est pas muni d'une structure riemannienne appropriée, d'ailleurs difficilement spécifiable a priori. Il est donc franchement à déconseiller, même pour minimiser une fonction quadratique strictement convexe de deux variables. Toutefois, ses qualités théoriques font que l'algorithme sert de modèle à la famille des algorithmes à directions de descente ou de sauvegarde dans les algorithmes à régions de confiance.
Le principe de cet algorithme remonte au moins à Cauchy (1847)[1].
L'algorithme
Soient un espace hilbertien (produit scalaire noté et norme associée notée ) et une fonction différentiable. On note la différentielle de en et le gradient de en , si bien que pour tout direction , [2].
Algorithme du gradient — On se donne un point/itéré initial et un seuil de tolérance . L'algorithme du gradient définit une suite d'itérés , jusqu'à ce qu'un test d'arrêt soit satisfait. Il passe de à par les étapes suivantes.
- Simulation : calcul de .
- Test d'arrêt : si , arrêt.
- Calcul du pas par une règle de recherche linéaire sur en le long de la direction .
- Nouvel itéré :
En pratique, il faudra prendre ; la valeur nulle de cette tolérance a été admise uniquement pour simplifier l'expression des résultats de convergence ci-dessous.
Cet algorithme structurellement très simple repose sur le fait que, dans le voisinage d'un point , la fonction décroît le plus fortement dans la direction opposée à celle du gradient de en , à savoir dans la direction . De manière plus précise, cette affirmation exprime en termes suggestifs le fait que, si , la solution du problème d'optimisation
est la direction , orientée donc vers l'opposé du gradient[3].
La notion de direction de plus forte pente est en fait mal définie car elle dépend fortement du produit scalaire que l'on se donne sur l'espace hilbertien . En effet, si est un autre produit scalaire sur , il existe un opérateur linéaire continu auto-adjoint et défini positif tel que si bien que le gradient de en pour ce dernier produit scalaire s'écrit , ce qui montre explicitement la dépendance du gradient par rapport au produit scalaire. Il n'y a donc pas une unique direction de plus forte pente, ce qui n'apparaît pas clairement dans l'affirmation faite au début du paragraphe précédent. On peut même montrer que toute direction de descente de en , c'est-à-dire toute direction telle , est l'opposé du gradient de en pour un certain produit scalaire[4]. L'efficacité de l'algorithme du gradient dépendra donc du choix de ce produit scalaire.
Si , la direction est une direction de descente de en , puisque , si bien que pour tout assez petit, on a
.
Grâce à la recherche linéaire, tant que , l'algorithme fait décroître la fonction strictement à chaque itération :
L'algorithme du gradient peut s'utiliser lorsque l'espace vectoriel sur lequel est définie la fonction à minimiser est de dimension infinie[5]. Dans ce cas, l'algorithme n'est pas implémentable, mais son étude peut avoir un intérêt pour connaître son comportement en grande dimension ou pour en utiliser les propriétés de convergence à des fins théoriques.
L'algorithme du gradient peut s'interpréter comme la méthode d'Euler explicite de résolution de l'équation différentielle ordinaire (flot du gradient), avec un pas de discrétisation adapté à l'itération courante par la recherche linéaire.
Résultats de convergence
Problèmes quadratiques
On considère dans un premier temps le cas où le critère est une fonction quadratique strictement convexe, définie sur un espace euclidien (donc de dimension finie) :
où et est un opérateur auto-adjoint défini positif. Dans ce cas, l'algorithme du gradient avec recherche linéaire exacte (i.e., à chaque itération le critère est minimisé le long de la direction opposée au gradient) converge q-linéairement vers l'unique minimum du problème. De manière plus précise, on a le résultat de convergence suivant, qui utilise le conditionnement du hessien H du critère f, c'est-à-dire le rapport entre sa plus grande valeur propre et sa plus petite valeur propre ,
et la norme associée à H qui est définie par
Convergence sur une fonction quadratique strictement convexe — Soit f une fonction quadratique strictement convexe sur un espace euclidien, de hessien H. Utilisé pour minimiser cette fonction, l'algorithme du gradient ci-dessus, avec et recherche linéaire exacte, génère une suite convergeant q-linéairement vers l'unique minimum x* de f. Plus précisément, on a
Comme , l'estimation de la vitesse de convergence ci-dessus s'applique aussi à celle du critère f(x) vers sa valeur optimale f(x*).
Ce résultat pourrait paraître attrayant et laisser penser que l'algorithme du gradient est une méthode performante, mais en général, ce n'est pas le cas. D'une part, la convergence linéaire est une propriété relativement faible en optimisation différentiable, d'autant plus faible que le taux de convergence (ici ) est proche de 1. Cela se produit dans l'algorithme du gradient lorsque est grand, c'est-à-dire pour les problèmes mal conditionnés. À l'inverse, lorsque (i.e., le hessien est un multiple de l'identité), l'algorithme converge en 1 itération. On rappelle par ailleurs que pour minimiser une fonction quadratique strictement convexe, l'algorithme du gradient conjugué ou toute méthode directe de résolution du système linéaire associé trouve le minimum en un nombre fini d'opérations (en arithmétique exacte), alors que l'algorithme du gradient requiert en général un nombre infini d'itérations.
Exemples
Minimisation d'une fonction de 2 variables
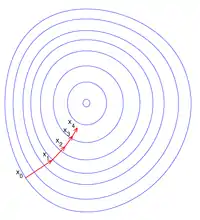
L'évolution des itérés au cours de l'algorithme est illustrée sur la figure de droite : f est une fonction convexe de deux variables (définie sur le plan ) et son graphe représente une forme de bol. Chaque courbe bleue représente une courbe de niveau de f, un lieu de points en lesquels f vaut une constante donnée. Chaque vecteur rouge représente un déplacement , qui est orienté suivant l'opposé de la direction du gradient en xk. Ici, le gradient en xk est celui associé au produit scalaire euclidien, si bien qu'il est orthogonal (pour le produit scalaire euclidien) à la tangente en xk à la courbe de niveau auquel xk appartient. La figure illustre la progression des itérés vers le fond du bol, c'est-à-dire vers le point où la valeur de f est minimale.
Maximisation d'une fonction de 2 variables
Application de la méthode de remontée de gradient à la fonction
.png.webp) Vue en plan avec courbes de niveaux
Vue en plan avec courbes de niveaux.png.webp) Vue en trois dimensions
Vue en trois dimensions
Une illustration de cette fonction trigonométrique, ci-dessus, permet de constater le caractère zigzagant de la méthode du gradient, dû au fait que le gradient d'un itéré est orthogonal au gradient du précédent. On notera que malgré la convergence de l'algorithme, cette dernière est relativement lente à cause de cette avancée en zigzag.
Problème de terminaison de l’algorithme à pas constant
Un défaut facilement observable de l'algorithme du gradient à pas constant, est sa non-convergence pour des pas trop élevés, ce même pour des fonctions qui en théorie devraient le faire converger. La fonction ci-dessous en est un cas typique. Dans la pratique avec un pas de 0.01 l'algorithme converge en moins 150 itérations. Mais si l'on décide d'opter pour un pas de 0.1, l'algorithme ne convergera tout simplement pas. On pourra vérifier que l'algorithme boucle entre les deux mêmes valeurs indéfiniment.
Points faibles, remèdes et extensions
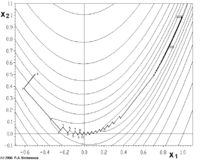
L'algorithme du gradient peut rencontrer un certain nombre de problèmes, en particulier celui de la convergence lorsque le minimum de la fonction se trouve au fond d'une vallée étroite (plus précisément lorsque le conditionnement de la matrice hessienne est élevée). Dans un tel cas, la suite des {xk} oscille de part et d'autre de la vallée et progresse laborieusement, même lorsque les αk sont choisis de sorte à minimiser f(b).
La figure ci-dessous illustre ce type de comportement pour une fonction de Rosenbrock à 2 dimensions.
Deux points faibles de l'algorithme du gradient sont :
- l'algorithme peut nécessiter de nombreuses itérations pour converger vers un minimum local, notamment si la courbure est très différente dans des directions différentes ;
- la recherche du pas α optimal, généralement effectuée par une recherche linéaire, peut se révéler très longue. Inversement, utiliser un pas α fixe peut conduire à de mauvais résultats. Des méthodes comme la méthode de Newton et l'inversion de la matrice hessienne en complément des techniques de gradient conjugué offrent souvent de meilleurs résultats.
Amélioration et alternatives dans le cas général
L’amélioration la plus naturelle de l’algorithme est la méthode de Newton avec recherche linéaire, dont la convergence est quadratique, et garantie si on dispose des hypothèses mentionnées dans Résultats de convergence.
Une alternative efficace est la méthode BFGS, qui consiste à calculer en chaque étape une matrice, qui multipliée au gradient permet d’obtenir une meilleure direction. De plus, cette méthode peut être combinée avec une méthode plus efficace de recherche linéaire afin d’obtenir la meilleure valeur de α.
L’algorithme du gradient est mal défini pour minimiser des fonctions non lisses, même si elles sont convexes. Lorsque le critère est localement lipschitzien, et spécialement s’il est convexe, l’algorithme des faisceaux apporte un remède à l’absence de convergence[6].
Notes et références
- Augustin Cauchy, « Méthode générale pour la résolution des systèmes d’équations simultanées », Comptes Rendus de l’Académie des Sciences de Paris, t. 25, , p. 536-538 (lire en ligne).
- M. Annad, A. Lefkir, M. Mammar-kouadri et I. Bettahar, « Development of a local scour prediction model clustered by soil class », Water Practice and Technology, no wpt2021065, (ISSN 1751-231X, DOI 10.2166/wpt.2021.065, lire en ligne, consulté le )
- Par l'inégalité de Cauchy-Schwarz la valeur optimale de ce problème est supérieure à , borne atteinte par la solution donnée.
- En effet, supposons que et que soit le gradient de en pour le produit scalaire . On considère l'application avec
- K. Ito, K. Kunisch (2008), Lagrange Multiplier Approach to Variational Problems and Applications, Advances in Design and Control, SIAM Publication, Philadelphia.
- (en) K. C. Kiwiel (2001), « Convergence and efficiency of subgradient methods for quasiconvex minimization », Mathematical Programming (Series A), 90, 1-25.
Voir aussi
Articles connexes
Bibliographie
- (en) Mordecai Avriel, Nonlinear Programming: Analysis and Methods, Dover Publishing, (ISBN 0-486-43227-0).
- (en) D. P. Bertsekas, Nonlinear Programming, Athena Scientific, (ISBN 1-886529-14-0)
- (en) J. F. Bonnans, J. Ch. Gilbert, C. Lemaréchal et C. Sagastizábal, Numerical Optimization - Theoretical and Numerical Aspects,
- (en) Jan A. Snyman, Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms, Springer Publishing, (ISBN 0-387-24348-8)
- Michel Bierlaire, Introduction à l'optimisation différentiable, (ISBN 978-2-88074-669-8)
- Marie-Hélène Meurisse, Algorithme numériques, Fondement théoriques et analyse pratique, Cours, exercices et applications avec MATLAB, (ISBN 9782340-021860)
- Patrick Lascaux et Raymond Théodor, Analyse numérique matricielle appliquée à l'art de l'ingénieur 2. Méthodes itératives,
- Jacques Rappaz et Marco Picasso, Introduction à l'analyse numérique,
Lien externe
J. Ch. Gilbert, Éléments d'Optimisation Différentiable — Théorie et Algorithmes, syllabus de cours à l'ENSTA ParisTech, Paris.




















































![\|x-x_*\|_H^2=2[f(x)-f(x_*)]](https://img.franco.wiki/i/6793b9494d4f9252de2575b96d010ae07284b686.svg)