Loi exponentielle

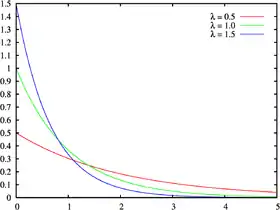
La densité de probabilité de la distribution exponentielle de paramètre λ > 0 prend la forme :

${\displaystyle f(x)=\left\{{\begin{matrix}\lambda \mathrm {e} ^{-\lambda x}&{\text{si}}\;x\geqslant 0\\0&{\text{si}}\;x<0\end{matrix}}\right.}$

La distribution a pour support l'intervalle ${\textstyle [0,+\infty [}$.

La fonction de répartition est donnée par :

${\displaystyle F(x)=\left\{{\begin{matrix}1-\mathrm {e} ^{-\lambda x}&{\text{si}}\;x\geqslant 0\\0&{\text{si}}\;x<0\end{matrix}}\right.}$

Densité d'une durée de vie d'espérance 10 de loi exponentielle ainsi que sa médiane.

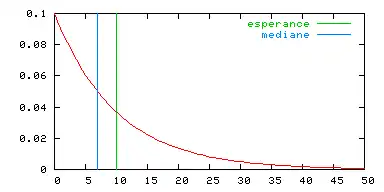
Soit X une variable aléatoire qui suit une loi exponentielle de paramètre λ.

Nous savons, par construction, que l'espérance mathématique de X est ${\displaystyle \mathbb {E} (X)={\frac {1}{\lambda }}}$.

On calcule la variance en intégrant par parties ; on obtient : ${\displaystyle V(X)={\dfrac {1}{\lambda ^{2}}}}$.

L'écart type est donc ${\displaystyle \sigma (X)={\dfrac {1}{\lambda }}}$.

La médiane, c'est-à-dire le temps T tel que ${\displaystyle \mathbb {P} (X>T)=0{,}5}$, est ${\displaystyle m={\dfrac {\ln(2)}{\lambda }}=\mathbb {E} (X)\ln(2)}$.

Le fait que la durée de vie soit sans vieillissement se traduit par l'égalité suivante :

${\displaystyle \forall T\geq 0,\qquad \mathbb {P} _{X>T}(X>T+t)=\mathbb {P} (X>t),}$

Par le théorème de Bayes on a :

${\displaystyle \mathbb {P} _{X>T}(X>T+t)={\dfrac {\mathbb {P} (X>T{\text{ et }}X>T+t)}{\mathbb {P} (X>T)}}={\dfrac {\mathbb {P} (X>T+t)}{\mathbb {P} (X>T)}}}$

En posant ${\displaystyle \mathbb {P} (X>t)=1-F(t)=G(t)}$ la probabilité que la durée de vie soit supérieure à t, on trouve donc :

${\displaystyle {\dfrac {G(T+t)}{G(T)}}=G(t)}$

Puisque la fonction G est monotone et bornée, cette équation implique que G est une fonction exponentielle. Il existe donc k réel tel que pour tout t :

${\displaystyle G(t)=\mathrm {e} ^{kt}.}$

Notons que k est négatif, puisque G est inférieure à 1. La densité de probabilité f est définie, pour tout t ≥ 0, par :

${\displaystyle f(t)=-k\mathrm {e} ^{kt}}$

Le calcul de l'espérance de X, qui doit valoir ${\displaystyle \mathbb {E} (X)}$ conduit à l'équation :

${\displaystyle \int _{0}^{+\infty }-kt\mathrm {e} ^{kt}\,\mathrm {d} t=\mathbb {E} (X)}$

On calcule l'intégrale en intégrant par parties ; on obtient :

${\displaystyle k=-{\dfrac {1}{\mathbb {E} (X)}}=-\lambda }$

Donc

${\displaystyle \mathbb {P} (X>t)=\mathrm {e} ^{-{\frac {t}{\mathbb {E} (X)}}}}$

et

${\displaystyle f(t)={\dfrac {1}{\mathbb {E} (X)}}\mathrm {e} ^{-{\frac {t}{\mathbb {E} (X)}}}}$

Une propriété importante de la distribution exponentielle est la perte de mémoire ou absence de mémoire. Cette propriété se traduit mathématiquement par l'équation suivante :

${\displaystyle \forall \ s,t\geq 0~\qquad \mathbb {P} _{T>t}(T>s+t)=\mathbb {P} (T>s)}$

Imaginons que T représente la durée de vie d'une ampoule à LED avant qu'elle ne tombe en panne : la probabilité qu'elle dure au moins s + t heures sachant qu'elle a déjà duré t heures sera la même que la probabilité de durer s heures à partir de sa mise en fonction initiale. En d'autres termes, le fait qu'elle ne soit pas tombée en panne pendant t heures ne change rien à son espérance de vie à partir du temps t. Il est à noter que la probabilité qu'une ampoule « classique » (à filament) tombe en panne ne suit une loi exponentielle qu'en première approximation, puisque le filament s'évapore lors de l'utilisation, et vieillit.

Si les variables aléatoires X, Y sont indépendantes et suivent deux lois exponentielles de paramètres respectifs λ, μ, alors Z = inf(X ; Y) est une variable aléatoire qui suit la loi exponentielle de paramètre λ + μ.

Démonstration

${\displaystyle {\begin{aligned}P(\min(X,Y)\leqslant t)~&=~1-P(\min(X,Y)>t)~\\&{\underset {X,Yind}{=}}~1-P(X>t)P(Y>t)~\\&=~1-(1-P(X\leqslant t))(1-P(Y\leqslant t))~\\&=~1-\mathrm {e} ^{-\lambda t}\mathrm {e} ^{-\mu t}~\\&=~1-\mathrm {e} ^{-(\lambda +\mu )t}~\\\\&\mathrm {donc} ~\min(X,Y)\thicksim {\mathcal {E}}(\lambda +\mu )\end{aligned}}}$

Parmi les lois de probabilités continues de support positif et de moyenne μ, la loi exponentielle de paramètre λ = 1/μ a la plus grande entropie différentielle. En d'autres termes, c'est la loi de probabilité d'entropie maximale pour une variable aléatoire positive d'espérance fixée[1].

Un domaine privilégié de la loi exponentielle est le domaine de la radioactivité (Rutherford et Soddy). Chaque atome radioactif possède une durée de vie qui suit une loi exponentielle. Le paramètre λ s'appelle alors la constante de désintégration.

La durée de vie moyenne ${\displaystyle {\dfrac {1}{\lambda }}}$ s'appelle le temps caractéristique.

La loi des grands nombres permet de dire que la concentration d'atomes radioactifs va suivre la même loi. La médiane ${\displaystyle {\dfrac {\ln(2)}{\lambda }}}$ correspond au temps T nécessaire pour que la population passe à 50 % de sa population initiale et s'appelle la demi-vie ou période.

On modélise aussi fréquemment la durée de vie d'un composant électronique par une loi exponentielle. La propriété de somme permet de déterminer l'espérance de vie d'un système constitué de deux composants en série.

En théorie des files d'attente, l'arrivée de clients dans une file est souvent modélisée par une loi exponentielle, par exemple dans le modèle de la file M/M/1.

En physique nucléaire, l'interaction d'une particule traversant un milieu avec celui-ci est décrite par une loi exponentielle. La probabilité d'interaction par unité de longueur d'une particule avec les atomes du milieu est donnée par la section efficace macroscopique ${\displaystyle n\,\sigma }$, avec ${\displaystyle n}$ la densité volumique d'atomes et ${\displaystyle \sigma }$ la section efficace microscopique.

Si ${\displaystyle X}$ est la variable aléatoire représentant la distance parcourue par la particule jusqu'à ce qu'elle interagisse avec un atome, la probabilité d'atteindre une distance ${\displaystyle x+dx}$ est la conjonction de deux événements que l'on suppose indépendants :

• la particule a parcourue la distance ${\displaystyle x}$ sans être absorbée, la probabilité de cet événement étant notée ${\displaystyle \mathbb {P} (X>x)}$;
• la particule n'a pas été absorbée lors de la traversée de la tranche élémentaire ${\displaystyle dx}$ du milieu, la probabilité de cet événement étant ${\displaystyle 1-n\,\sigma \,dx}$.

Du fait de l'hypothèse d'indépendance, la probabilité recherchée est donc :

${\displaystyle \mathbb {P} (X>x+dx)=\mathbb {P} (X>x)\,(1-n\,\sigma \,dx)}$

En passant à la limite

${\displaystyle \lim _{dx\rightarrow 0}{\frac {\mathbb {P} (X>x+dx)-\mathbb {P} (X>x)}{dx}}={\frac {d\mathbb {P} }{dx}}=-\mathbb {P} (X>x)\,n\,\sigma }$

Puisque ${\displaystyle \mathbb {P} (X>0)=1}$, cette équation différentielle linéaire d'ordre un à coefficient constant admet pour solution :

${\displaystyle \mathbb {P} (X>x)={\rm {e}}^{-n\,\sigma \,x}}$

Soit encore

${\displaystyle \mathbb {P} (X<x)=1-{\rm {e}}^{-n\,\sigma \,x}}$

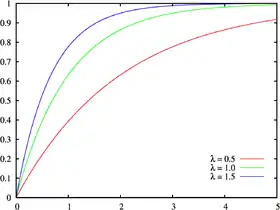
ce qui est la fonction de répartition d'une loi exponentielle de paramètre ${\displaystyle \lambda =n\,\sigma }$. Par suite, l'espérance de cette loi

${\displaystyle \ell ={\frac {1}{n\,\sigma }}}$

est aussi appelée libre parcours moyen de la particule dans le milieu.

La loi géométrique est une version discrétisée de la loi exponentielle. En conséquence, la loi exponentielle est une limite de lois géométriques renormalisées.

Propriété — Si X suit la loi exponentielle d'espérance 1, et si ${\displaystyle Y=\lceil \theta X\rceil ,\ \theta >0,\ }$ alors Y suit la loi géométrique de paramètre

${\displaystyle p=1-\mathrm {e} ^{-{\tfrac {1}{\theta }}}}$

Démonstration

${\displaystyle {\begin{aligned}\mathbb {P} (Y=k)&=\mathbb {P} (\lceil \theta X\rceil =k)\\&=\mathbb {P} (\theta X\in \ ]k-1,k])\\&=\mathbb {P} \left(X\in \left]{\tfrac {k-1}{\theta }},{\tfrac {k}{\theta }}\right]\right)\\&=F_{X}\left({\tfrac {k}{\theta }}\right)-F_{X}\left({\tfrac {k-1}{\theta }}\right)\\&=\exp \left(-{\tfrac {k-1}{\theta }}\right)-\exp \left(-{\tfrac {k}{\theta }}\right)\\&=\left(\mathrm {e} ^{-{\tfrac {1}{\theta }}}\right)^{k-1}\ \left(1-\mathrm {e} ^{-{\tfrac {1}{\theta }}}\right).\end{aligned}}}$

Notons que, pour un nombre réel x, ${\displaystyle \lceil x\rceil \ }$ désigne la partie entière supérieure de x, définie par

${\displaystyle \lceil x\rceil =\min \left\{k\in \mathbb {Z} \ |\ k\geq x\right\}.}$

En choisissant

${\displaystyle \theta =-{\tfrac {\lambda }{\ln \left(1-p\right)}},}$

on fabrique ainsi, à partir d'une variable aléatoire exponentielle X ' de paramètre λ une variable aléatoire

${\displaystyle Y^{\prime }=\lceil \theta X^{\prime }\rceil }$

,

suivant une loi géométrique de paramètre p arbitraire (avec toutefois la contrainte 0 < p < 1), car X=λX' suit alors une loi exponentielle de paramètre 1 (et d'espérance 1).

Réciproquement,

Propriété — Si, pour ${\displaystyle n\geq 1}$, la variable aléatoire Y_n suit la loi géométrique de paramètre p_n, et si

${\displaystyle \lim _{n}p_{n}=0,\qquad \lim _{n}p_{n}/a_{n}=\lambda >0,}$

alors a_nY_n converge en loi vers la loi exponentielle de paramètre λ.

Démonstration

On se donne une variable aléatoire exponentielle λ de paramètre 1, et on pose

${\displaystyle {\begin{aligned}\theta _{n}&=-{\tfrac {1}{\ln \left(1-p_{n}\right)}},\\Y_{n}^{\prime }&=\lceil \theta _{n}X\rceil .\end{aligned}}}$

Alors Y_n et Y_n ' ont même loi, en vertu de la propriété précédente. Par ailleurs, pour tout ω

${\displaystyle \lim _{n}a_{n}Y_{n}^{\prime }(\omega )=\lim _{n}a_{n}\lceil \theta _{n}X(\omega )\rceil =\left(\lim _{n}a_{n}\theta _{n}\right)X(\omega )=X(\omega )/\lambda }$

Or d'une part la convergence presque sûre entraine la convergence en loi, d'autre part la loi de X/λ est la loi exponentielle de paramètre λ.

On peut voir ces différentes convergences comme de simples conséquences de la convergence du schéma de Bernoulli vers le processus de Poisson.

La loi exponentielle est une loi de Weibull avec un facteur de forme k (ou β) de 1.

• Variables aléatoires élémentaires
• Variable aléatoire
• Loi géométrique