Libre parcours moyen

Figure 1: Tranche de cible.

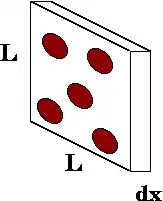
On considère un faisceau de particules projetées vers une cible, ainsi qu'une tranche infinitésimale de cette cible (Figure 1). Les atomes (ou autres particules) susceptibles d'arrêter des particules du faisceau sont en rouge. La grandeur du libre parcours moyen dépend des caractéristiques du système auquel la particule appartient :

${\displaystyle \ell ={\frac {1}{\sigma n}},}$

Où ${\displaystyle \ell }$ est le libre parcours moyen, ${\displaystyle n}$ la quantité de particules-cible par unité de volume, et ${\displaystyle \sigma }$ la section efficace de collision.

L'aire d'une tranche est ${\displaystyle L^{2}}$ et son volume est ${\displaystyle L^{2}\,{\rm {d}}x}$.

La quantité de particules incidentes contenues dans cette tranche est le produit de la concentration ${\displaystyle n}$ par le volume, c'est-à-dire, ${\displaystyle nL^{2}\,{\rm {d}}x}$.

La probabilité ${\displaystyle P(x)\,{\rm {d}}x}$ qu'une particule incidente soit arrêtée par cette tranche est l'aire totale recouverte par les atomes cibles, divisée par l'aire totale de la tranche.

${\displaystyle P(x)\,{\rm {d}}x={\frac {\mathrm {Aire_{atomes}} }{\mathrm {Aire_{tranche}} }}={\frac {\sigma nL^{2}\,{\rm {d}}x}{L^{2}}}=n\sigma \,{\rm {d}}x}$

où ${\displaystyle \sigma }$ est l'aire, ou, plus formellement, la section efficace d'un atome.

La diminution d'intensité du faisceau passant à travers une tranche est égale à l'intensité du faisceau incident multipliée par la probabilité de collision.

${\displaystyle {\rm {d}}I=-In\sigma \,{\rm {d}}x}$

C'est une équation différentielle linéaire :

${\displaystyle {\frac {{\rm {d}}I}{{\rm {d}}x}}=-In\sigma \ {\stackrel {\mathrm {def} }{=}}\ -{\frac {I}{\ell }}}$

dont la solution est connue sous le nom de Loi de Beer-Lambert et a pour forme ${\displaystyle I=I_{0}e^{-x/\ell }}$, où ${\displaystyle x}$ est la distance parcourue par le faisceau à travers la cible et ${\displaystyle I_{0}}$ est l'intensité du faisceau avant d'avoir pénétré la cible. ${\displaystyle l}$ est appelé « libre parcours moyen » parce qu'il est égal à la distance moyenne parcourue par une particule du faisceau avant d'être arrêtée. On peut le comprendre en remarquant que la probabilité qu'une particule soit absorbée entre ${\displaystyle x}$ et ${\displaystyle x+{\rm {d}}x}$ est donnée par :

${\displaystyle P(x)\,{\rm {d}}x={\frac {I(x)-I(x+{\rm {d}}x)}{I_{0}}}={\frac {1}{\ell }}e^{-x/\ell }{\rm {d}}x.}$

Ainsi la valeur moyenne attendue pour ${\displaystyle x}$ est :

${\displaystyle \langle x\rangle \ {\stackrel {\mathrm {def} }{=}}\ \int _{0}^{\infty }x\,{\rm {d}}P(x)=\int _{0}^{\infty }{\frac {x}{\ell }}e^{-x/\ell }{\rm {d}}x=\ell }$

La fraction des particules n'étant pas stoppées par la tranche est appelée la transmittance ${\displaystyle T={\frac {I}{I_{0}}}=e^{-x/\ell }}$ où ${\displaystyle x}$ est l'épaisseur traversée.

Dans la théorie élémentaire de la cinétique des gaz le libre parcours moyen d'une particule, telle qu'une molécule, est la distance moyenne parcourue entre deux collisions successives avec d'autres particules en mouvement supposées assimilables à des sphères rigides parfaitement élastiques.

La formule ${\displaystyle \ell ={\frac {1}{n\sigma }}}$ est toujours valable pour une particule ayant une vitesse relative élevée parmi un ensemble de particules identiques distribuées aléatoirement dans l'espace. Dans le cas où la distribution des vitesses est conforme à la loi de distribution des vitesses de Maxwell, le résultat suivant s'applique[2]

${\displaystyle \ell ={\frac {1}{{\sqrt {2}}\,n\sigma }}.\,}$

et on peut montrer que le libre parcours moyen est également [3]

${\displaystyle \ell ={\frac {k_{\rm {B}}T}{{\sqrt {2}}\pi d^{2}p}}}$

où ${\displaystyle k_{\text{B}}}$ est la constante de Boltzmann en J/K, ${\displaystyle T}$ la température en K, ${\displaystyle p}$ la pression en pascals, et ${\displaystyle d}$ le diamètre des particules constituant le gaz (en mètres).

Le tableau suivant donne quelques valeurs typiques pour l'air à différentes pressions et à température ambiante.

Libre parcours moyen pour des photons de 1 keV à 20 MeV et des éléments de numéro atomique Z = 1 à 100. Basé sur des données tirées de NIST[4]. Les discontinuités sont dues à la faible densité des éléments gazeux. Six bandes correspondent aux voisinages de 6 gaz nobles.

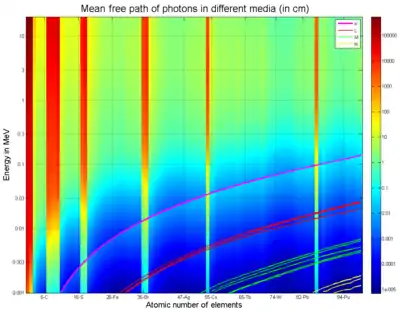
En radiographie par rayons gamma, le libre parcours moyen d'un faisceau de photons monochromatiques est la distance moyenne qu'un photon parcourt avant d'entrer en collision avec des atomes du matériau cible. Il dépend de la nature dudit matériau et de l'énergie des photons selon

${\displaystyle \ell ={\frac {1}{\mu }}={\frac {1}{(\mu /\rho )\rho }},}$

où ${\displaystyle \mu }$ est le coefficient d'absorption, ${\displaystyle \mu /\rho }$ est le coefficient d'absorption massique et ${\displaystyle \rho }$ la masse volumique du matériau. Le coefficient d'absorption massique peut être récupéré ou calculé pour un certain matériau et une énergie donnée à partir des bases de données du NIST [5] - [6]

En radiographie par rayons X le calcul du libre parcours moyen est plus complexe, car les photons n'ont pas une seule et même énergie et forment en fait un spectre.

Alors que les photons se déplacent à travers le matériau cible, ils sont atténués avec des probabilités dépendant de leur énergie, modifiant ainsi leur spectre. À cause de cela, le libre parcours moyen d'un spectre X-ray dépend de la longueur de matériau traversée.

L'épaisseur d'un matériau est parfois mesurée en nombre de libre parcours moyen ${\displaystyle \ell }$. Les matériaux avec une épaisseur d'un ${\displaystyle \ell }$ atténuent ${\displaystyle 1/e\simeq 37\ \%}$ des photons. Ce concept est étroitement lié à la couche de demi-atténuation (CDA). Un matériau avec une CDA de 1 atténuera 50 % des photons.

En physique des particules, le concept de libre parcours moyen n'est pas couramment utilisé. On privilégie le concept similaire de longueur d'atténuation, c'est-à-dire l'épaisseur d'un matériau pour laquelle 63 % du rayonnement incident est absorbé.

En particulier, pour des photons de haute énergie, qui interagissent principalement par production de paires électron-positron, on parle plutôt de Longueur de radiation, qui ressemble beaucoup au libre parcours moyen en radiographie.

Si l'on considère un gaz de particules n'absorbant pas la lumière de diamètre d et de fraction volumique ${\displaystyle \Phi }$, le libre parcours moyen[7] des photons est donné par :

${\displaystyle \ell ={\frac {2d}{3\Phi Q_{s}}}}$,

où ${\displaystyle Q_{s}}$, le coefficient d'efficacité de diffusion, peut être évalué numériquement pour des particules sphériques à l'aide de la théorie de Mie.

Dans une cavité vide de volume ${\displaystyle V}$ et de surface intérieure ${\displaystyle S}$, le libre parcours moyen d'une particule rebondissant sur ses parois est :

${\displaystyle \ell ={\frac {4V}{S}}}$

Une application classique du libre parcours moyen est l'estimation de la taille des atomes ou des molécules.

Une autre application importante est une estimation de la résistivité d'un matériau à partir du libre parcours moyen de ses électrons.

Par exemple, pour des ondes sonores confinées, le libre parcours moyen est la distance moyenne parcourue par une onde avant réflexion.

En aérodynamique, le libre parcours moyen est du même ordre de grandeur que l'épaisseur d'une onde de choc à des nombres de mach supérieurs à 1.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Mean free path » (voir la liste des auteurs).