Cercle trigonométrique
En mathématiques, le cercle trigonométrique est un cercle qui permet d'illustrer et de définir des notions comme celles d'angle, de radian et les fonctions trigonométriques : cosinus, sinus, tangente. Il s'agit du cercle dont le rayon est égal à 1 et qui est centré sur l'origine du repère, dans le plan usuel muni d'un repère orthonormé.
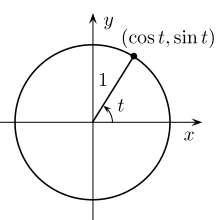
Fonctions trigonométriques sur le cercle
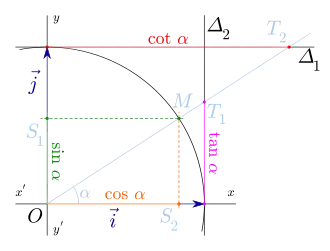
Soit un repère orthonormé du plan euclidien.
Soit M un point du cercle trigonométrique de coordonnées (x, y) et son vecteur associé. Si un réel t est une mesure de l'angle alors .
et l'équation cartésienne du cercle donne immédiatement une identité trigonométrique connue :
Le cercle trigonométrique peut aussi donner un moyen intuitif de réaliser que les fonctions sinus et cosinus sont des fonctions périodiques, vérifiant les relations :
Ces égalités s'interprètent par le fait que le point (x, y) reste le même après avoir ajouté ou retranché un multiple entier de 2π et ainsi effectué plusieurs tours complets du cercle. Lorsqu'elles sont définies à partir d'un triangle rectangle, les valeurs des fonctions sinus, cosinus et d'autres fonctions trigonométriques n'ont de sens que pour des angles compris entre 0 et π/2 rad, mais dans le cercle trigonométrique leurs valeurs prennent un sens en n'importe quel réel.
Le rapporteur est un instrument de mesure matérialisant le cercle trigonométrique.
Valeurs remarquables

| Angle centésimal | 0° | 33,3° | 50° | 66,7° | 100° | 133,3° | 150° | 166,7° | 200° | 233,3° | 250° | 266,7° | 300° | 333,3° | 350° | 366,7° | 400° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Angle sexagésimal | 0 | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| Angle en radians | |||||||||||||||||
| Cosinus (axe x) | |||||||||||||||||
| Sinus (axe y) |
(Les personnes intéressées par un tableau plus complet peuvent consulter les valeurs trigonométriques exactes en bibliothèque wikiversitaire)
Le cercle trigonométrique et le repérage polaire
Le cercle trigonométrique est un cas particulier simple de la représentation en coordonnées polaires d'un point M du plan. Au couple de composantes cartésiennes (x, y), on substitue un couple (r, θ), où r est la distance, positive, de M à l'origine, et θ une mesure en radians de l'angle orienté . Cette approche permet alors de définir le cercle trigonométrique comme le lieu des points vérifiant en coordonnées polaires r = 1.































