Première bissectrice
En mathématiques, la première bissectrice est une droite du plan muni d’un repère orthonormé, caractérisée par l’équation y = x. Il s’agit de la bissectrice du premier et du troisième quadrants, c’est-à-dire les secteurs délimités par les demi-droites portées par les axes du repère et ayant des abscisses et ordonnées de même signe. Son équation montre aussi qu’elle représente la fonction identité dans l’ensemble des fonctions réelles.
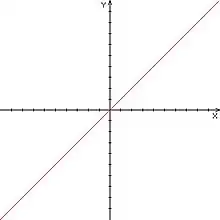
De même, la deuxième bissectrice est caractérisée par l’équation y = −x. Cette bissectrice des deuxième et quatrième quadrants représente l’opposé de la fonction identité.
La symétrie par rapport à la première bissectrice échange les axes de coordonnées. Elle transforme donc la courbe d’une fonction injective sur celui de sa réciproque.
Cette droite permet aussi de visualiser les suites récurrentes réelles simples définies par une relation de récurrence de la forme un+1 = f(un), où f est une fonction réelle d'une variable réelle.
En trigonométrie, la première bissectrice correspond à un angle polaire de π/4 radians, c’est-à-dire 45°, donc à une pente de 1.
En statistique, la première bissectrice définit une répartition strictement égalitaire pour la courbe de Lorenz.
Dans un diagramme de Penrose-Carter, la première bissectrice correspond à une ligne de lumière.