Paradoxe des anniversaires

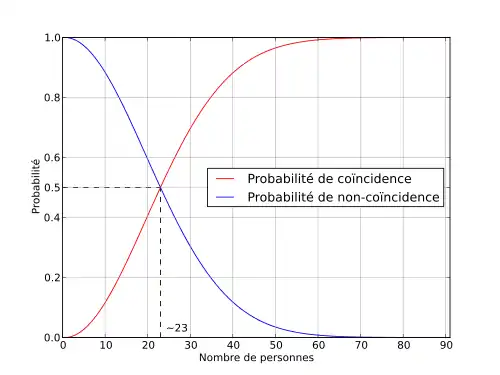
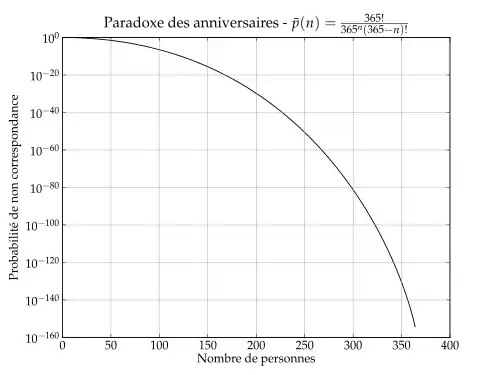
Le paradoxe des anniversaires résulte de l'estimation probabiliste du nombre de personnes que l'on doit réunir pour avoir au moins une chance sur deux que deux personnes de ce groupe aient leur anniversaire le même jour. Il se trouve que ce nombre est 23[1], ce qui choque un peu l'intuition. À partir d'un groupe de 57 personnes, la probabilité est supérieure à 99 %.

Il s'agit d'un paradoxe non pas dans le sens de contradiction logique, mais dans le sens où c'est une vérité mathématique qui contredit l'intuition : la plupart des gens estiment que cette probabilité est très inférieure à 50 %.

Cette étude est due à Richard von Mises.

Comprendre le problème

Par souci de simplicité, l'article est rédigé en supposant que toutes les années sont non bissextiles. Prendre en compte le 29 février changerait peu les résultats, mais rendrait les calculs très délicats.

Signification intuitive

Le problème des anniversaires revient à choisir un nombre n d'éléments dans un ensemble qui en comprend N, sans retrait ; c'est-à-dire sans retirer les éléments choisis, si bien que certains peuvent être identiques. Le paradoxe des anniversaires est bien un cas de ce type, car chacun a une date d'anniversaire plus ou moins aléatoire, et il n'y a pas a priori de raison autre que la probabilité pour que deux dates soient identiques ou différentes.

Imaginez par exemple qu'au cours d'une soirée réunissant n personnes, des petits papiers, sur lesquels sont notés les nombres de 1 à N, soient placés dans une corbeille. Chacun à son tour tire un papier, lit le nombre qu'il porte, puis le replace dans la corbeille. Quelles sont les chances pour que 2 nombres tirés au moins soient identiques ? ou au contraire pour que tous soient différents ?

Pour calculer la probabilité numérique, il est plus simple de compter les chances que tous les nombres soient différents. Le point-clé non évident qui induit notre intuition en erreur, concerne au contraire les chances que 2 nombres au moins soient identiques. Au bout du compte, les deux approches sont bien sûr équivalentes.

Si l'on considère un nombre tiré donné, quelles sont ses chances d'être identique à un autre ? Il peut être égal à n'importe quel autre ; en revanche, le nombre total de possibilités restreint ses chances : on a donc intuitivement une chance proportionnelle à $n / N$ . Mais cette chance-là s'applique à tous les nombres tirés, si bien qu'à la fin, la chance qu'un nombre tiré quelconque soit identique à n'importe quel autre nombre tiré est dans une proportion d'environ $n 2 / N$ . C'est là que notre intuition est trompée, et on prédit une probabilité de 50 % pour n proche de $N /2$ alors que $\sqrt N$ est une meilleure approximation.

Cela revient à dire que l’on confond la question posée : les chances de n’importe quel élément choisi d’être identique à n’importe quel autre, avec une autre question proche : les chances de n’importe quel élément choisi d’être identique à un autre élément donné. Dans le cas des anniversaires, on tend à évaluer intuitivement la probabilité pour que la date d’anniversaire de quiconque soit la même qu’une date d’anniversaire donnée (par exemple, la mienne) ; au lieu de la probabilité pour que la date d’anniversaire de quiconque soit la même que celle de n’importe qui d’autre.

Reste à savoir pourquoi notre intuition est ainsi trompée, c’est-à-dire pourquoi elle ne semble pas spontanément capable d’aborder correctement un problème de ce type. C’est une question pour les sciences cognitives.

Démonstration

Nous donnons une preuve pour le cas d'origine, avec des jours d'anniversaires, mais cela se transpose simplement au cas de la généralisation énoncée. Une erreur fréquente dans la démonstration est de compter le nombre de paires, on omet alors le fait que les évènements ne sont pas disjoints et que trois personnes peuvent bien partager la même date de naissance : ces évènements ne sont pas disjoints. Le plus simple pour obtenir le résultat annoncé est de calculer la probabilité que chaque personne ait un jour anniversaire différent de celui des autres : le contraire de ce que l’on cherche.

On peut procéder par récurrence : la première personne a donc 365 choix, la deuxième 364, la troisième 363, la quatrième 362, et ainsi de suite. On va ici procéder par dénombrement, c'est-à-dire, que nous allons compter le nombre de cas où n personnes ont des jours d'anniversaires différents et nous diviserons par le nombre de possibilités. Dans les deux cas nous faisons une hypothèse d'équiprobabilité des jours de naissance.

Il y a $n$ personnes, pour chacune il y a 365 jours possibles, donc au total si on ne se fixe aucune contrainte, il y a $365 n$ possibilités. Si maintenant on veut des jours différents, nous obtenons un arrangement de $n$ parmi 365, soit : $A_{365}^{n}=(365-0)(365-1)...(365-n+1)={\frac {365!}{(365-n)!}}$ .

On a donc

{\overline {p}}(n)={\frac {365!}{(365-n)!}}\cdot {\frac {1}{365^{n}}}

On peut également le voir comme une multiplication de probabilités d'évènements indépendants :

{\overline {p}}(n)=\underbrace {{\frac {365}{365}}\cdot {\frac {364}{365}}\cdot {\frac {363}{365}}\cdot \cdots \cdot {\frac {365-n+1}{365}}} _{n\,{\text{ facteurs}}}

Or, l’évènement « un jour anniversaire différent par personne » est le complémentaire de « au moins deux identiques ». Par conséquent la probabilité recherchée est $p(n)=1-{\overline {p}}(n)$ .

En faisant l'application numérique, on trouve 50,73 % de chances pour deux dates anniversaires identiques dans une assemblée de vingt-trois personnes.

Probabilité de coïncidence de 2 anniversaires en fonction du nombre de personnes.

n	p(n)
5	2,71 %
10	11,69 %
15	25,29 %
20	41,14 %
23	50,73 %
25	56,87 %
30	70,63 %
40	89,12 %
50	97,04 %
60	99,41 %
80	99,99 %
100	99,99997 %
200	99,9999999999999999999999999998 %
300	$\left(1-\left(6\cdot 10^{-82}\right)\right)\cdot 100\%$
350	$\left(1-\left(3\cdot 10^{-131}\right)\right)\cdot 100\%$
> 366	100 % (par le principe des tiroirs) si on prend en compte la possibilité d'être né le 29 février.

Probabilité de non-coïncidence de 2 anniversaires en fonction du nombre de personnes.

Généralisation

Ce paradoxe des anniversaires se généralise à la situation plus abstraite que l'on peut énoncer sous la forme :

Soit $E$ un ensemble fini de cardinal $N$ . La probabilité $p(n)$ que, parmi $n$ éléments de $E$ , chaque élément étant tiré uniformément dans tout l'ensemble $E$ , deux éléments au moins soient identiques vaut :

p(n)=1-{\frac {N!}{(N-n)!}}\cdot {\frac {1}{N^{n}}}

Approximation de la probabilité

La probabilité ${\overline {p}}(n)=1-p(n)$ peut se réécrire sous la forme :

{\overline {p}}(n)=\prod _{k=0}^{n-1}(N-k)/N

, d'où

{\overline {p}}(n)=\left(1-{\frac {1}{N}}\right)\left(1-{\frac {2}{N}}\right)...\left(1-{\frac {n-1}{N}}\right)

Or, on a le développement limité ${\rm {e}}^{x}=1+x+o(x)$ pour x voisin de 0. Cela conduit à l'approximation :

{\overline {p}}(n)\approx \prod _{k=0}^{n-1}{\rm {e}}^{-{\frac {k}{N}}}

{\overline {p}}(n)\approx {\rm {e}}^{-{\frac {\sum _{k=0}^{n-1}k}{N}}}

Or, la somme des entiers de 0 à $n-1$ vaut $n(n-1)/2$ , ce qui donne finalement :

{\overline {p}}(n)\approx {\rm {e}}^{-{\frac {n(n-1)}{2\cdot N}}}

En revenant à $p(n)$ :

p(n)\approx 1-{\rm {e}}^{-{\frac {n(n-1)}{2\cdot N}}}

Estimation du nombre de tirages pour une probabilité donnée

L'approximation de $n(p)$ permet d'obtenir simplement une approximation du nombre de personnes nécessaire pour avoir une probabilité donnée $p$ d'avoir au moins deux personnes avec le même jour d'anniversaire. On obtient ainsi :

n(p)\approx {\sqrt {2\cdot N\ln \left({\frac {1}{1-p}}\right)}}

Quelques valeurs numériques

Le tableau ci-dessous indique dans le cas originel ( $N=365$ ), pour une probabilité $p$ , l'approximation $n(p)$ , puis, sur la même ligne, l'approximation de la probabilité pour l'entier inférieur ou égal à $n(p)$ (noté $\lfloor n\rfloor$ ) et celle de probabilité pour l'entier supérieur ou égal à $n(p)$ (noté $\lceil n\rceil$ ). Normalement, la probabilité $p$ fixée au départ doit être comprise entre ces deux valeurs. Les entrées ne vérifiant pas cette condition sont signalées en couleur.

$p$	$n$	$\lfloor n\rfloor$	$p(\lfloor n\rfloor )$	$\lceil n\rceil$	$p(\lceil n\rceil )$
0,01	2,70864	2	0,00274	3	0,00820
0,05	6,11916	6	0,04046	7	0,05624
0,1	8,77002	8	0,07434	9	0,09462
0,2	12,76302	12	0,16702	13	0,19441
0,3	16,13607	16	0,28360	17	0,31501
0,5	22,49439	22	0,47570	23	0,50730
0,7	29,64625	29	0,68097	30	0,70632
0,8	34,27666	34	0,79532	35	0,81438
0,9	40,99862	40	0,89123	41	0,90315
0,95	46,76414	46	0,94825	47	0,95477
0,99	57,98081	57	0,99012	58	0,99166

Lien avec la loi de Rayleigh

Dans l'expression :

p(n)\approx 1-{\rm {e}}^{-{\frac {n(n-1)}{2\cdot 365}}},

on reconnaît la fonction de répartition de la loi de Rayleigh :

F(x)=1-{\rm {e}}^{-{\frac {x^{2}}{2}}}.

En effet, vu dans le cadre plus général des problèmes d'allocation, le calcul ci-dessus s'interprète comme la convergence d'une fonction de répartition vers une autre, traduisant la convergence en loi d'une suite de variables aléatoires : considérons m boîtes numérotées de 1 à m, m étant, pour l'instant, fixé. Supposons qu'on y alloue des boules, chaque boule étant placée dans une des m boîtes de manière équiprobable, indépendamment des allocations précédentes, et cela indéfiniment. Si m=365, ceci est la situation du problème des anniversaires pour un groupe de personnes qui s'agrandit régulièrement. On note $T_{m}$ le rang de la première boule qui est allouée dans une boite contenant déjà une autre boule, ce qui correspondrait au rang de la première personne, arrivant dans le groupe, dont la date anniversaire est déjà celle d'un autre membre du groupe (avant son arrivée tous les membres du groupe ont des dates d'anniversaires différentes, après son arrivée ce n'est plus le cas). Alors

p(n)=\mathbb {P} (T_{365}\leq n),

Et l'approximation ci-dessus peut donc s'écrire :

\mathbb {P} (T_{365}/{\sqrt {365}}\leq x)\approx 1-{\rm {e}}^{-{\frac {x^{2}}{2}}}.

Cela traduit le fait que la suite de variables aléatoires $T_{m}/{\sqrt {m}}$ converge en loi vers la loi de Rayleigh, et, par là même, cela révèle un paradoxe, pour le sens commun : on s'attend probablement à ce que $T_{m}$ soit du même ordre de grandeur que m, alors que cette convergence en loi révèle que $T_{m}$ est du même ordre de grandeur que ${\sqrt {m}}.$ Le phénomène de répétition des anniversaires a donc lieu plus tôt, pour un groupe plus petit qu'on ne s'y attendrait.

Cas non uniforme

Dans le calcul précédent, l'équirépartition des jours de naissance dans l'année a été supposée implicitement. Que se passe-t-il si on ne la suppose plus ? La réponse est que cela augmente les chances de réussir le pari que deux personnes soient nées le même jour, ce qui renforce encore le paradoxe.

Démonstration de ce fait.

Comme la démonstration se fera par récurrence sur le nombre de jours dans l'année, nous notons $n$ ce nombre, et $k\leqslant n$ le nombre de personnes ; soit $X_{j}$ la variable aléatoire donnant la date anniversaire de la personne n° $j$ . De façon naturelle les variables $X_{j}$ sont supposées indépendantes de même loi : $P\left(X_{j}=i\right)=x_{i}$ , indépendant de $j$ .

L'évènement cherché (les personnes sont nées des jours différents) est la réunion des évènements disjoints $\{(X_{1},...,X_{k})=(i_{1},..,i_{k})\},(i_{1},..,i_{k})$ étant un arrangement de $[\!\left[1,n\right]\!]$ .

La probabilité recherchée est donc

p_{k}(x_{1},..,x_{n})=\sum _{(i_{1},..,i_{k})~{\text{arrangement de }}[\!\left[1,n\right]\!]}x_{i_{1}}\cdot x_{i_{2}}\cdot ...\cdot x_{i_{k}}=k!{\underset {1\leqslant i_{1}<..<i_{k}\leqslant n}{\sum }}x_{i_{1}}\cdot x_{i_{2}}...\cdot x_{i_{k}}

Comme annoncé, nous allons démontrer que pour tout $k$ entre 2 et $n$ ,

p_{k}(x_{1},..,x_{n})\leqslant p_{k}(1/n,...,1/n){\text{   si    }}\sum _{i=1}^{n}x_{i}=1,x_{i}\geqslant 0

Posant $\varphi _{k}(x_{1},..,x_{n})=\sum _{1\leqslant i_{1}<..<i_{k}\leqslant n}x_{i_{1}}.x_{i_{2}}....x_{i_{k}}$ , nous allons même plus généralement démontrer par récurrence sur $n$ que pour tout $k$ entre 2 et $n$ :

\varphi _{k}(x_{1},..,x_{n})\leqslant \varphi _{k}(s/n,...,s/n){\text{   si    }}\sum _{i=1}^{n}x_{k}=s,x_{i}\geqslant 0

Pour $n=2$ , la seule possibilité pour $k$ est $k=2$ , et l'inégalité $\varphi _{2}\left(x_{1},x_{2}\right)=x_{1}x_{2}\leqslant \left({\dfrac {x_{1}+x_{2}}{2}}\right)^{2}$ est facile.

Supposons la propriété vraie à l'ordre $n$ et montrons-la à l'ordre $n+1$ .

Posons $\sum _{k=1}^{n+1}x_{k}=s$ et $x_{n+1}=x$ .

Remarquons que $\varphi _{k}\left(x_{1},...,x_{n},x\right)=x\varphi _{k-1}(x_{1},..,x_{n})+\varphi _{k}(x_{1},..,x_{n})$ .

Par hypothèse de récurrence,

\varphi _{k-1}(x_{1},..,x_{n})\leqslant \varphi _{k-1}\left({\dfrac {s-x}{n}},...,{\dfrac {s-x}{n}}\right)={\binom {n}{k-1}}\left({\dfrac {s-x}{n}}\right)^{k-1}

\varphi _{k}(x_{1},..,x_{n})\leqslant \varphi _{k}\left({\dfrac {s-x}{n}},...,{\dfrac {s-x}{n}}\right)={\binom {n}{k}}\left({\dfrac {s-x}{n}}\right)^{k}

On obtient donc $\varphi _{k}\left(x_{1},...,x_{n},x\right)\leqslant x{\binom {n}{k-1}}\left({\dfrac {s-x}{n}}\right)^{k-1}+{\binom {n}{k}}\left({\dfrac {s-x}{n}}\right)^{k}$ .

Soit

\varphi _{k}\left(x_{1},...,x_{n},x\right)\leqslant {\dfrac {1}{kn^{k}}}{\binom {n}{k-1}}\left[knx\left(s-x\right)^{k-1}+\left(n-k+1\right)\left(s-x\right)^{k}\right]

Posant $y=s-x$ , la dernière parenthèse vaut

f\left(y\right)=kn\left(s-y\right)y^{k-1}+\left(n-k+1\right)y^{k}=knsy^{k-1}-\left(n+1\right)\left(k-1\right)y^{k}

La dérivée $f'(y)=k(k-1)y^{k-2}(ns-(n+1)y)$ montre que $f$ est maximale pour $y={\dfrac {n}{n+1}}s$ , soit $x={\dfrac {s}{n+1}}$ .

Donc $\varphi _{k}\left(x_{1},...,x_{n},x\right)\leqslant {\dfrac {s}{n+1}}{\binom {n}{k-1}}\left({\dfrac {s}{n+1}}\right)^{k-1}+{\binom {n}{k}}\left({\dfrac {s}{n+1}}\right)^{k}={\binom {n+1}{k}}\left({\dfrac {s}{n+1}}\right)^{k}$ $=\varphi _{k}\left({\dfrac {s}{n+1}},...,{\dfrac {s}{n+1}}\right)$ , ce qui achève la récurrence.

Remarquons que cela revient à démontrer que l'espérance du produit de $k$ nombres distincts pris parmi $n$ nombres positifs de somme donnée est maximale quand ces $n$ nombres sont égaux.

Géométriquement : parmi tous les hyperparallélépipèdes rectangles (ou orthotopes) de dimension $n$ de somme des longueurs des arêtes donnée, celui qui a la plus grande moyenne des hypervolumes des $k$ -cellules est l'hypercube. Pour $n=3,k=2$ ou 3 : parmi tous les parallélépipèdes rectangles de somme des longueurs des arêtes données, celui qui a la plus grande aire (ou volume) est le cube.

Applications

Dans Le Trésor des Paradoxes (Éd Belin, 2007), les auteurs notent que l’informaticien américain Robert Mac Eliece a établi l'intérêt du paradoxe des anniversaires en informatique, pour s’assurer de la fiabilité des mémoires d’ordinateur, grâce à des codes détecteurs d’erreurs, fondés notamment sur les travaux de Richard Hamming aux laboratoires Bell. La stratégie des codes détecteurs d’erreurs s’avère, du point de vue statistique, similaire au paradoxe des anniversaires. Le paradoxe des anniversaires est utilisé en cryptographie pour élaborer des attaques sur les fonctions de hachage. Une des contraintes imposées sur ces fonctions, pour une utilisation cryptographique, est de produire peu de collisions, autrement dit, de rarement prendre la même valeur sur des entrées différentes.

Le paradoxe des anniversaires donne une borne sur le nombre moyen d'éléments nécessaires pour avoir une collision avec une probabilité $p={\frac {1}{2}}$ , à savoir essentiellement la racine carrée du nombre de valeurs possibles pour la fonction de hachage, sous l'hypothèse que cette fonction est uniformément distribuée sur ses valeurs d'arrivée.

Plus concrètement, si une fonction de hachage a une sortie de N bits alors l'ensemble d'arrivée possède $2^{N}$ éléments et il faut environ $2^{\frac {N}{2}}$ hachés d'éléments distincts pour produire une collision avec 50 % de chance ; les sorties de la fonction pouvant être comparées à des personnes avec des anniversaires se répartissant sur $2^{N}$ valeurs.

Application pratique de l'attaque des anniversaires

Supposons que Martine souhaite forcer Daniel à signer un contrat très défavorable, contrat devant être validé par son empreinte (valeur hashée), celle-ci garantissant que le contrat n'a pas pu être modifié après signature.

Elle prépare un contrat équitable, et un contrat défavorable. Elle génère ensuite automatiquement des variantes de chacun des contrats avec des changements cosmétiques (ajouts d'espaces, utilisation de synonymes, ré-ordonnancement des paragraphes, etc). Elle calcule l’empreinte de chaque contrat en recherchant des paires de mêmes empreintes (avec et sans modifications). Dès qu’une collision a été trouvée, elle donne le contrat équitable correspondant à Daniel qui le vérifie, le signe, calcule l'empreinte et l'attache au contrat.

Martine fait de même avec le contrat défavorable, et le présente à Daniel. S'il conteste les termes du contrat qu'il a signé, l'empreinte prouve qu'il est impossible qu'il ait pu être modifié[2]. Il lui sera tout de même possible d'opposer le contrat original à Martine ce qui devrait conduire à la nullité du contrat.

Lien avec l'identification par l'ADN

Dans le domaine judiciaire, les probabilités d'identification fournies par la technique d'empreinte génétique sont souvent mal comprises[3]. Ainsi, si la probabilité que deux individus partagent neuf locus est environ d'une sur 13 milliards on peut s'attendre à ce que dans une base de données de 65 000 personnes, environ 116 paires d'individus aient en commun 9 des 13 locus utilisés à des fins d'identification[3].

Anecdote

Dans Le Livre qui rend fou[4], Raymond Smullyan raconte qu'il a fait établir la formule à ses 19 élèves. Il conclut après application numérique qu'il y a nettement moins d'une chance sur deux (un peu moins de 38 %) pour que deux élèves aient leur anniversaire le même jour. Un élève lui répond qu'il parie que c'est tout de même le cas. Le professeur fait l'appel en demandant aux élèves de donner leur date de naissance, et éclate de rire avant la fin, suivi de toute la classe, en se souvenant que deux de ses élèves sont jumeaux.

Notes et références

Ross 2014, p. 37.
« Attaque « des anniversaires » »
Leila Schneps et Coralie Colmez (trad. de l'anglais par Coralie Colmez), Les maths au tribunal : les erreurs de calcul font les erreurs judiciaires [« Math on Trial. How Numbers Get Used and Abused in the Courtroom »], Paris, Seuil, coll. « Science ouverte », 280 p. (ISBN 978-2-02-110439-4), chap. 5 (« L'affaire Diana Sylvester : analyse d'un cold hit »).
Smullyan 1982, p. 6.

Annexes

Bibliographie

[Ross 2014] (en) Sheldon Ross, A First Course in Probability, Pearson, 2014, 467 p. (ISBN 978-0-321-79477-2 et 032179477X), chap. 2.
[Smullyan 1982] (en) Raymond Smullyan, The Lady or the Tiger? [« Le Livre qui rend fou »], 1982, 226 p. (ISBN 0-8129-2117-8).

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.