Bijection de Joyal

Notons ${\displaystyle {\mathcal {C}}_{n}}$ l'ensemble des arbres de Cayley à n sommets. Pour calculer le cardinal de ${\displaystyle {\mathcal {C}}_{n},}$ une des démonstrations consiste à établir une bijection, appelée bijection de Joyal, entre ${\displaystyle {\mathcal {C}}_{n}\times [\![1,n]\!]^{2}}$ et l'ensemble des applications de ${\displaystyle [\![1,n]\!]}$ dans ${\displaystyle [\![1,n]\!]}$, noté usuellement ${\displaystyle [\![1,n]\!]^{[\![1,n]\!]}}$. On a ainsi

${\displaystyle n^{n}\ =\ {\text{Card}}\ [\![1,n]\!]^{[\![1,n]\!]}\ =\ {\text{Card}}\ \left({\mathcal {C}}_{n}\times [\![1,n]\!]^{2}\right)\ =\ n^{2}\,{\text{Card}}\ {\mathcal {C}}_{n}.}$

Cette démonstration est attribuée à André Joyal par Aigner et Ziegler[1], ou encore par Pitman[2].

On peut voir ${\displaystyle {\mathcal {C}}_{n}\times [\![1,n]\!]^{2}}$ comme l'ensemble des arbres de Cayley à n sommets, dont deux sommets sont marqués, de deux marques différentes. Le sommet portant la première marque peut être interprété comme la racine de l'arbre. Les deux marques différentes peuvent être portées par le même sommet.

La bijection de Joyal permet aussi de mieux comprendre la topologie d'un arbre de taille n, en étudiant la distance entre 2 sommets au hasard d'un arbre au hasard. En effet, un élément tiré au hasard avec équiprobabilité dans ${\displaystyle \Omega ={\mathcal {C}}_{n}\times [\![1,n]\!]^{2}}$ est un arbre de Cayley, avec deux points marqués, tiré au hasard : calculer la loi de différentes statistiques portant sur un arbre de Cayley, avec deux points marqués, tiré au hasard, revient à calculer le cardinal de différentes parties de l'univers ${\displaystyle \Omega ={\mathcal {C}}_{n}\times [\![1,n]\!]^{2}.}$ Pour cela il peut être plus simple de calculer le cardinal de l'image de ces parties par la bijection de Joyal.

Représentation graphique de l'application ƒ = (12, 15, 2, 13, 10, 10, 13, 9, 19, 17, 18, 12, 15, 16, 20, 14, 2, 2, 13, 8).

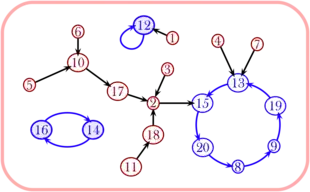
Pour décrire la bijection de Joyal, il est commode d'utiliser une représentation de chaque application ƒ de ${\displaystyle [\![1,n]\!]}$ dans ${\displaystyle [\![1,n]\!]}$ à l'aide d'un graphe orienté dont l'ensemble des sommets est ${\displaystyle [\![1,n]\!],}$ et où les arêtes relient chaque élément à son image par ƒ[3]. Par exemple, pour ƒ = (12, 15, 2, 13, 10, 10, 13, 9, 19, 17, 18, 12, 15, 16, 20, 14, 2, 2, 13, 8), c'est-à-dire pour ƒ(1) = 12, ƒ(2) = 15, ƒ(3) = 2, … on a la représentation graphique ci-contre.

Dans l'ensemble de définition de ƒ on peut distinguer les éléments cycliques (ou récurrents) des éléments transitoires (ou transients) : les éléments cycliques, figurés ci-contre en bleu, sont les éléments x pour lesquels il existe n_x > 0 tel que :

${\displaystyle f^{n_{x}}(x)=x.}$

Par exemple, ci-contre, n₁₂ = 1, n₁₆ = 2, et n₈ = 6. À chaque application ƒ de ${\displaystyle [\![1,n]\!]}$ dans ${\displaystyle [\![1,n]\!],}$ on peut associer la chaîne de Markov dont la probabilité de transition est définie par

${\displaystyle p_{i,f(i)}=1,\qquad \forall i\in [\![1,n]\!].}$

Les éléments récurrents et les éléments transitoires de ƒ sont alors exactement les éléments récurrents et les éléments transitoires de cette chaîne de Markov.

Correspondance de Foata appliquée à la restriction τ de ƒ à C. Les deux points marqués de l'arbre de Cayley (associé à ƒ par la correspondance de Foata) sont ici 9 et 14.

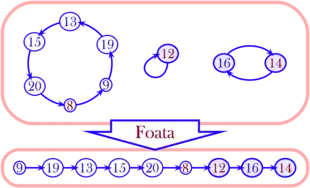
L'ensemble C des éléments cycliques de ƒ est le plus grand sous-ensemble de ${\displaystyle [\![1,n]\!]}$ ayant la propriété suivante:

• la restriction de ƒ à C est une bijection de C dans C.

On peut alors appliquer la correspondance de Foata à la restriction de ƒ à C, que nous noterons τ, et obtenir ainsi un arrangement (une suite ordonnée) ω de tous les éléments de C. La correspondance de Foata consiste à écrire la suite des cycles de la décomposition en cycles disjoints de τ, en prenant bien soin :

• de terminer chacun de ces cycles par son plus petit élément,
• d'écrire les dits cycles dans l'ordre croissant de leurs plus petits éléments.

Le premier et le dernier terme de l'arrangement ω ainsi obtenu sont destinés à être les deux sommets marqués de l'arbre de Cayley produit, à partir de ƒ, par la bijection de Joyal.

Image de l'application ƒ par la bijection de Joyal. Le « début » (x = 9) est coloré en vert, et la « fin » (y = 14) en orange.

Image réciproque, par la bijection de Joyal, de l'arbre marqué obtenu en intervertissant les deux marques de l'arbre précédent.

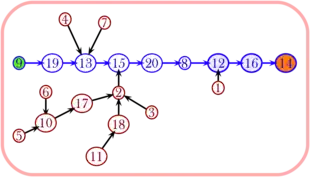
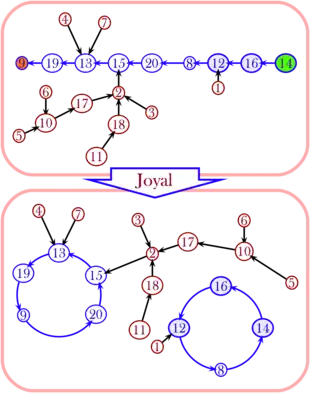
On observe qu'une fois effacées les arêtes entre les éléments cycliques de ƒ, la représentation de ƒ ainsi modifiée devient une forêt (un graphe sans cycles, éventuellement non connexe, dont les composantes connexes sont précisément des arbres), chaque arbre de la forêt pouvant être vu comme enraciné en un des éléments cycliques de ƒ. En « replantant » chacun de ces arbres sur le sommet correspondant du graphe linéaire associé à l'arrangement de tous les éléments de C produit par la correspondance de Foata, on obtient un arbre de Cayley avec deux sommets marqués.

Réciproquement, la donnée d'un arbre de Cayley T avec deux points x et y marqués, éventuellement égaux, l'un marqué « début » et l'autre « fin », par exemple, définit

• une orientation de chaque arête de T (par exemple, chaque arête de T est orientée du sommet le plus éloigné de la fin (y) vers le sommet le plus proche de y) ;
• un unique chemin de longueur minimale de x à y (il existe un chemin car un arbre est un graphe connexe, il existe un seul chemin minimal car un arbre est un graphe sans cycle) ;
• une suite ordonnée de nombres de ${\displaystyle [\![1,n]\!],}$ notée ω : la suite des labels des sommets apparaissant sur le chemin de longueur minimale entre x et y, lorsque ce chemin est parcouru de x à y. La suite ω commence donc par le label du sommet x et se termine donc par le label du sommet y. La longueur de la suite ω peut éventuellement être strictement inférieure à n.

À cette suite ω on peut appliquer la correspondance de Foata, pour trouver une permutation τ des nombres constituant ω, permutation dont le graphe est une collection de cycles. Ces cycles sont délimités par les records vers le bas de la suite obtenue en renversant la suite ω, i.e. les records observés en parcourant le chemin de y vers x.

Sur l'exemple ci-contre, x = 9 et y = 14, et le chemin minimal est ω = (9, 19, 13, 15, 20, 8, 12, 16, 14). Les records de la suite renversée (14, 16, 12, 8, 20, 15, 13, 19, 9) sont successivement 14, 12 et 8, ce qui conduit à la décomposition de τ en cycles disjoints :

${\displaystyle \tau \ =\ (9,19,13,15,20,8)(12)(16,14).}$

On retrouve bien ainsi les cycles de ƒ.

Une fois effacées les arêtes composant le chemin de longueur minimale entre x et y, l'arbre de Cayley T ainsi modifié devient une forêt, chaque arbre de la forêt pouvant être vu comme enraciné en un des sommets du chemin entre x et y. En « replantant » chacun de ces arbres sur le sommet correspondant du graphe de τ, on obtient le graphe de ƒ.

À titre d'exemple, si l'on intervertit les rôles de x et y, on obtient un nouvel élément de ${\displaystyle {\mathcal {C}}_{n}\times [\![1,n]\!]^{2}.}$ Examinons son image réciproque g par la bijection de Joyal : l'ensemble des étiquettes des sommets apparaissant sur le chemin de y à x reste le même, mais la suite η obtenue est la suite inverse de la suite ω observée précédemment. Les records vers le bas de la suite renversée de η (à savoir la suite ω) sont alors 9 puis 8, conduisant à une décomposition en cycles (14, 16, 12, 8) (20, 15, 13, 19, 9) de la partie cyclique de g. On récupère alors, comme attendu, une application g = (12, 15, 2, 13, 10, 10, 13, 14, 20, 17, 18, 8, 19, 16, 13, 12, 2, 2, 9, 15) différente de l'application ƒ qu'on avait au départ (voir ci-dessus).

Comme autre application, on peut citer le calcul de la loi de la distance ${\displaystyle D_{n}}$ entre deux points au hasard d'un arbre de Cayley aléatoire, qui, en vertu de la bijection de Joyal, est aussi la loi du nombre de points cycliques d'une application de ${\displaystyle [\![1,n]\!]}$ dans ${\displaystyle [\![1,n]\!]}$. Notons ${\displaystyle d_{n,k}}$ le nombre d'éléments de ${\displaystyle {\mathcal {C}}_{n}\times [\![1,n]\!]^{2}}$ tels que les deux points marqués soient à distance k l'un de l'autre. Pour ${\displaystyle 0\ \leq \ k\ \leq \ n-1,}$ on a :

${\displaystyle d_{n,k}\ =\ {n \choose k+1}\times (k+1)!\times n^{n-k-1}\times {\frac {k+1}{n}},}$

où ${\displaystyle {n \choose k+1}}$ compte les choix possibles de l'ensemble des étiquettes des k + 1 points sur le chemin entre les deux points marqués, où ${\displaystyle (k+1)!}$ compte les manières d'ordonner ces k + 1 étiquettes le long du chemin entre les deux points marqués, le facteur restant comptant les forêts de k + 1 arbres comportant au total n – k – 1 sommets (sans compter les k + 1 racines) qu'on pourrait planter le long de ce chemin. Il suit que, toujours pour ${\displaystyle 0\ \leq \ k\ \leq \ n-1,}$

${\displaystyle \mathbb {P} \left(D_{n}=k\right)\ =\ n^{-n}d_{n,k}\ =\ {\frac {(k+1)\times (n)_{\downarrow k+1}}{n^{k+2}}}.}$

Cette loi discrète apparaît aussi dans des problèmes d'allocations (boules et urnes), dont le fameux problème des anniversaires. On peut montrer, par exemple à l'aide du lemme de Scheffé, que ${\displaystyle D_{n}/{\sqrt {n}}}$ converge en loi vers la loi de Rayleigh, ce qui indique que la distance « typique » entre deux points d'un arbre de taille n est de l'ordre de ${\displaystyle {\sqrt {n}}.}$