Pseudo-forêt

Les noms évoquent l'analogie avec les arbres et les forêts plus couramment étudiés : un arbre est un graphe connexe sans cycle ; une forêt est une union disjointe d'arbres. Gabow et Tarjan[1] attribuent l'étude des pseudo-forêts au livre de 1963 de Dantzig sur la programmation linéaire, livre dans lequel les pseudo-forêts apparaissent dans la solution de certains problèmes de réseaux de flot[2]. Les pseudo-forêts forment également des modèles graphiques de fonctions et apparaissent dans plusieurs problèmes algorithmiques. Les pseudo-forêts sont des graphes creux – le nombre de leurs arêtes est borné linéairement par le nombre de sommets (en fait, ils ont au plus d'arêtes qu'ils ont de sommets) – et leur structure matroïde permet de décomposer plusieurs autres familles de graphes creux en des unions de forêts et de pseudo-forêts. Le nom « pseudo-forêt » vient d'un article de Picard et Queyranne[3] en 1982.

Les 21 graphes unicycliques avec au plus six sommets

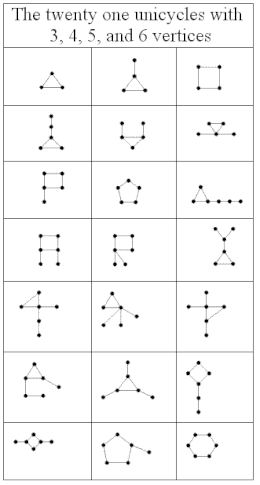
On considère ici des graphes ou multigraphes non orientés avec boucles. Une pseudo-forêt est un graphe non orienté dans lequel chaque composante connexe contient au plus un cycle[4]. De manière équivalente, il s'agit d'un graphe non orienté dans lequel chaque composante connexe n'a pas plus d'arêtes que de sommets[5]. Les composantes sans cycle sont des arbres ; les composantes qui ont un cycle sont appelés 1-arbres ou graphes unicycliques . Autrement dit, un 1-arbre est un graphe connexe contenant exactement un cycle. Une pseudo-forêt avec une seule composante connexe est appelée un pseudo-arbre ; c'est soit un arbre ou un 1-arbre; en général, une pseudo-forêt peut avoir plusieurs composants connexes qui sont toutes des arbres ou 1-arbres.

Si l'on enlève à un 1-arbre l'une des arêtes de son cycle, le résultat est un arbre. Réciproquement, si l'on augmente un arbre en connectant deux de ses sommets par une nouvelle arête, le résultat est un 1-arbre ; la chaîne dans l'arbre reliant les deux extrémités de l'arête ajoutée, ainsi que l'arête ajoutée elle-même, forment le cycle unique du 1-arbre. Si ajoute à un 1-arbre une arête qui relie l'un de ses sommets à un sommet nouveau, le résultat est à nouveau un 1-arbre, avec un sommet de plus ; une méthode pour construire les 1-arbres consiste donc à commencer par un seul cycle, puis à répéter l'opération d'augmentation un nombre arbitraire de fois. Les arêtes de n'importe quel 1-arbre peuvent être divisées de manière unique en deux sous-graphes, dont l'un est un cycle et l'autre est une forêt, de sorte que chaque arbre de la forêt contient exactement un sommet du cycle[6].

Certaines familles plus particulières de pseudo-forêts ont également été étudiés :

• Une 1-forêt, parfois appelée pseudo-forêt maximale, est une pseudo-forêt à laquelle on ne peut ajouter une arête sans qu'une composante du graphe contienne plusieurs cycles. Si une pseudo-forêt contient un arbre comme l'une de ses composantes, ce n'est pas une 1-forêt, car on peut ajouter soit une arête reliant deux sommets à l'intérieur de cet arbre, formant un seul cycle, soit une arête reliant cet arbre à une autre composante. Ainsi, les 1-forêts sont exactement les pseudo-forêts dans lesquelles chaque composante est un 1-arbre.
• Les pseudo-forêts couvrantes d'un graphe non orienté G sont les sous-graphes de G qui contiennent tous les sommets de G et qui sont des pseudo-forêts. Une telle pseudo-forêt n'a pas besoin d'avoir d'arêtes, puisque par exemple le sous-graphe qui contient tous les sommets de G et aucune arête est une pseudo-forêt (dont les composants sont des arbres constitués d'un seul sommet).
• Les pseudo-forêts maximales de G sont les sous-graphes de G qui sont des pseudo-forêts qui ne sont contenus dans aucune pseudo-forêt plus grande de G . Une pseudo-forêt maximale de G est toujours une pseudo-forêt couvrante, mais la réciproque est fausse. Si G n'a pas de composante connexe qui est un arbres, alors ses pseudo-forêts maximales sont des 1-forêts, mais si G a un composante qui est un arbre, ses pseudo-forêts maximales ne sont pas des 1-forêts. Plus précisément, dans tout graphe G, ses pseudo-forêts maximales sont constituées de chaque composante de G qui est un arbre, et de 1-arbres disjoints couvrant les sommets restants de G .

• Des versions orientées de ces définitions sont également utilisées pour les graphes orientés. Une pseudo-forêt orientée est un graphe orienté dans lequel chaque sommet a au plus un arc sortant ; c'est-à-dire qu'il a un degré sortant 0 ou 1. Une 1-forêt dirigée — plus souvent appelée un graphe fonctionnel ou des fois pseudo-forêt orientée maximale — est un graphe orienté dans lequel le degré sortant est exactement égal à un[7]. Si D est une pseudo-forêt orientée, le graphe non orienté formé en supprimant la direction de chaque arête de D est une pseudo-forêt non orientée.

Une fonction de l'ensemble {0,1,2,3,4,5,6,7,8} dans lui-même, et son graphe fonctionnel.

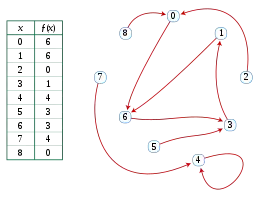
Les pseudo-forêts orientées et les endo-fonctions sont en un sens équivalentes. Toute fonction ƒ d'un ensemble X dans lui-même (c'est-à-dire un endomorphisme de X ) peut être vue comme définissant une pseudo-forêt orientée qui a une arête de x à y si et seulement si ƒ( x ) = y . La pseudo-forêt orientée résultante est maximale et contient une boucle pour chaque x tel que ƒ( x ) = x . Réciproquement, toute pseudo-forêt orientée maximale détermine une fonction ƒ telle que ƒ( x ) est l'extrémité terminale de l'arc sortant de x, et toute pseudo-forêt orientée non maximale peut être rendue maximale en ajoutant des boucles puis convertie dans une fonction de la même manière. Pour cette raison, les pseudo-forêts maximales orientées sont parfois appelées graphes fonctionnels[1]. Le tracé d'une fonction sous la forme d'un graphe fonctionnel fournit un cadre pratique pour décrire des propriétés qui ne sont pas aussi faciles à décrire du point de vue de la théorie des fonctions ; cette technique est particulièrement adaptée aux problèmes impliquant des fonctions itérées, qui correspondent à des cheminements dans les graphes fonctionnels.

La détection de cycle est le problème algorithmique qui consiste à suivre un chemin dans un graphe fonctionnel pour y trouver un cycle ; ce problème a des applications en cryptographie et en théorie algorithmique des nombres, dans le cadre de algorithme rho de Pollard pour la factorisation d'entiers et en tant que méthode pour détecter des collisions dans les fonctions de hachage cryptographiques . Dans ces applications, on s'attend à ce que ƒ se comporte de manière aléatoire ; Flajolet et Odlyzko[13] étudient les propriétés théoriques des graphes fonctionnels issus de fonctions tirées au hasard. En particulier, une forme du paradoxe des anniversaires implique que, dans un graphe fonctionnel aléatoire à n sommets, le chemin partant d'un sommet sélectionné au hasard revient en général sur lui-même pour former un cycle en O( √n ) pas. Koniaguine et al. ont fait des progrès analytiques et informatiques sur les statistiques des graphes[14].

Martin, Odlyzko et Wolfram[15] étudient les pseudo-forêts qui modélisent la dynamique des automates cellulaires. Ces graphes fonctionnels, qu'ils appellent diagrammes de transition d'états, ont un sommet pour chaque configuration de l'ensemble des cellules de l'automate, et une arête reliant une configuration à la configuration suivante si elle est obtenue par l'application des règles de l'automate. On peut déduire certaines propriétés de l'automate à partir de la structure de ces diagrammes, telles que le nombre de composantes, la longueur des cycles limites, la profondeur des arbres reliant des états non limites à ces cycles, ou les symétries du diagramme. Par exemple, tout sommet sans arête entrante correspond à un jardin d'Éden et un sommet avec une boucle automatique correspond à une structure stable.

Une autre application déjà ancienne des graphes fonctionnels concerne les « trains » utilisés pour étudier des les systèmes triples de Steiner[16] . Le train d'un système triple est un graphe fonctionnel ayant un sommet pour chaque triplet possible de symboles ; chaque triplet pqr est envoyé par ƒ sur le triplet stu, où pqs, prt et qru sont les triplets qui appartiennent au système et contiennent respectivement les paires pq, pr, et qr . Les trains se sont avérés être un invariant puissant des systèmes triples, bien qu'ils sont un peu lourds à calculer.

Un matroïde est une structure mathématique dans laquelle certains ensembles d'éléments sont définis comme indépendants ; les ensembles indépendants satisfont des propriétés modelées sur les propriétés d'indépendance linéaire dans un espace vectoriel. L'un des exemples standard de matroïde est le matroïde graphique dans lequel les ensembles indépendants sont les ensembles d'arêtes dans les forêts d'un graphe ; la structure matroïde des forêts est importante dans les algorithmes de calcul de l'arbre couvrant de poids minimal du graphe. De manière analogue, on peut définir des matroïdes à partir de pseudo-forêts.

Pour tout graphe G = ( V, E ), on peut définir un matroïde sur les arêtes de G, dans lequel un ensemble d'arêtes est indépendant si et seulement s'il forme une pseudo-forêt ; ce matroïde est appelé matroïde bicirculaire (ou matroïde bicyclique) de G[17] - [18]. Les plus petits ensembles dépendants pour ce matroïde sont les sous-graphes connexes minimaux de G qui ont plus d'un cycle, et ces sous-graphes sont parfois appelés bicycles. Il existe trois types de bicycles possibles : un graphe thêta qui a deux sommets reliés par trois chemins dont les sommets internes sont disjoints , un graphe en 8 qui se compose de deux cycles qui ont un seul sommet en commun, et un graphe menottes qui est formé de deux cycles disjoints reliés par une chaîne [19]. Un graphe est une pseudo-forêt si et seulement s'il ne contient pas de bicycle comme sous-graphe.

Le graphe papillon (à gauche) et le graphe diamant (à droite), sont des mineurs interdits pour les pseudo-forêts.

Un mineur d'une pseudo-forêt est obtenu en contractant certaines de ses arêtes et en supprimant d'autres ; le résultat est une autre pseudo-forêt. Par conséquent, la famille des pseudo-forêts est fermée par passage aux mineurs, et le théorème de Robertson-Seymour implique que les pseudo-forêts peuvent être caractérisées en termes d'un ensemble fini de mineurs exclus, de manière analogue au théorème de Wagner qui caractérise les graphes planaires comme les graphes n'ayant ni le graphe complet K ₅ ni le graphe biparti complet K _3,3 comme mineurs. Comme indiqué ci-dessus, un graphe qui n'est pas une pseudo-forêt contient comme sous-graphe une menotte, la graphe en 8 ou un graphe thêta ; un graphe menottes ou un graphe en 8 peut être contracté pour former un graphe papillon (graphe en 8 à cinq sommets), et un graphe thêta peut être contracté pour former un graphe diamant (graphe thêta à quatre sommets), donc tout graphe qui n'est pas une pseudo-forêt contient en mineur soit un papillon, soit un diamant, et ce sont les seuls graphes mineurs-minimaux qui ne sont pas des pseudo-forêts. Ainsi, un graphe est une pseudo-forêt si et seulement s'il n'admet ni le papillon ni le diamant comme mineur. Si l'on interdit seulement le losange et pas le papillon, la plus grande famille de graphes qui en résulte se compose des graphes cactus et des unions disjointes de plusieurs graphes cactus[20].

Si l'on considère des multigraphes et on autorise des boucles, il n'y a qu'un seul mineur interdit, à savoir un sommet avec deux boucles.

Une des premières utilisations algorithmiques des pseudo-forêts est dans le cadre de l'algorithme du simplexe de réseau et son application aux problèmes de flots généralisés modélisant la conversion entre des produits de différents types[2] - [21]. Dans ces problèmes, on donne en entrée un réseau de flot dans lequel les sommets modélisent les produits et les arêtes modélisent les conversions admissibles entre produits. Chaque arête a plusieurs étiquettes : une capacité (la quantité de produit qui peut être converti en unité de temps), un multiplicateur (le taux de conversion entre les produits) et un coût (combien de perte ou, s'il est négatif, de profit par unité de conversion). L'objectif consiste à déterminer la quantité de chaque produit à convertir via chaque arête du réseau de flot, afin de minimiser les coûts ou de maximiser le profit, tout en respectant les contraintes de capacité et en ne permettant pas aux produits de s'accumuler s'ils sont inutilisés. Ce type de problème peut être formulé comme un programme linéaire et résolu en utilisant l'algorithme du simplexe. Les solutions intermédiaires issues de cet algorithme, ainsi que la solution optimale éventuelle, ont une structure particulière : chaque arête du réseau d'entrée est soit inutilisée soit utilisée à sa pleine capacité, à l'exception d'un sous-ensemble d'arêtes, formant une pseudo-forêt couvrante du réseau d'entrée, dont les débits peuvent être compris entre zéro et la pleine capacité. Dans cette application, les graphes unicycliques sont aussi parfois appelés arbres augmentés et les pseudo-forêts maximales sont aussi parfois appelées forêts augmentées[21].

Le problème de la pseudo-forêt couvrante minimale est de trouver une pseudo-forêt couvrante de poids minimum dans un graphe G plus grand pondéré aux arêtes. En vertu de la structure matroïde des pseudo-forêts, des pseudo-forêts maximales de poids minimum peuvent être trouvées par des algorithmes gloutons similaires à ceux du problème de l' arbre couvrant minimum. Cependant, Gabow et Tarjan ont trouvé une approche en temps linéaire plus efficace dans ce cas[1].

La pseudo-arboricité d'un graphe G est définie par analogie à l'arboricité comme le nombre minimum de pseudo-forêts dans lesquelles ses arêtes peuvent être partitionnées ; de manière formelle, c'est le plus petit entier k tel que G est ( k ,0)-parcimonieux, ou le plus petit k tel que les arêtes de G peuvent être orientées pour former un graphe orienté avec un degré extérieur au plus k . En raison de la structure matroïde des pseudo-forêts, la pseudo-arboricité peut être calculée en temps polynomial[22].

Un graphe biparti aléatoire avec n sommets dans chaque partie de sa bipartition, et avec cn arêtes choisies indépendamment et au hasard à partir de chacune des n ² paires de sommets possibles, est une pseudo-forêt avec forte probabilité lorsque c est une constante strictement inférieure à un. Ce fait joue un rôle clé dans l'analyse du hachage coucou (en), une structure de données permettant de rechercher des couples clé-valeur en cherchant dans l'une de deux tables de hachage à des emplacements déterminés à partir de la clé : on peut former un graphe, le « graphe coucou », dont les sommets correspondent aux places de la table de hachage et dont les arêtes relient les deux emplacements où l'une des clés pourrait être trouvée, et l'algorithme de hachage du coucou réussit à trouver des emplacements pour toutes ses clés si et seulement si le graphe coucou est une pseudo-forêt[23].

Les pseudo-forêts jouent également un rôle clé dans les algorithmes parallèles pour la coloration des graphes et les problèmes connexes[24].