Mineur (théorie des graphes)

Un graphe ${\displaystyle H}$ est un mineur du graphe fini et non orienté ${\displaystyle G}$ s'il peut être obtenu en contractant des arêtes d'un sous-graphe de ${\displaystyle G}$. En d'autres termes, ${\displaystyle H}$ peut être obtenu à partir de ${\displaystyle G}$ en effectuant un nombre quelconque d'opérations parmi les suivantes :

• suppression d'un sommet isolé ${\displaystyle x}$ : le sommet ${\displaystyle x}$ est supprimé du graphe ;
• suppression d'une arête ${\displaystyle xy}$ : on supprime l'arête ${\displaystyle xy}$, mais ses extrémités restent inchangées ;
• contraction d'une arête ${\displaystyle xy}$ : on supprime l'arête ${\displaystyle xy}$, les deux sommets ${\displaystyle x}$ et ${\displaystyle y}$ sont fusionnés en un sommet ${\displaystyle z}$. Toute arête ${\displaystyle tx}$ ou ${\displaystyle ty}$ est remplacée par une nouvelle arête ${\displaystyle tz}$. Une même arête n'est pas ajoutée deux fois (on ne crée pas d'arêtes parallèles).

Cette définition est celle qui est donnée par László Lovász[1]. On trouve des définitions différentes, mais équivalentes, dans la littérature.

• 
  Un graphe ${\displaystyle G}$.
• 
  Un mineur ${\displaystyle H}$ de ${\displaystyle G}$.
• 
  Passage de ${\displaystyle G}$ à ${\displaystyle H}$.

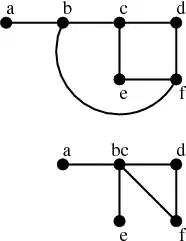
Dans l'exemple ci-dessus, on passe d'un graphe à son mineur en supprimant trois arêtes (en pointillés), en supprimant un sommet isolé et en contractant une arête (en gris).

Une des utilités du concept de mineur est la caractérisation de classes de graphes particulières comme ayant (ou n'ayant pas) un certain graphe comme mineur. Par exemple, un graphe planaire ne contient comme mineur ni ${\displaystyle K_{5}}$ (graphe complet d'ordre 5), ni ${\displaystyle K_{3,3}}$ (graphe biparti complet d'ordre 3). Le théorème de Robertson-Seymour montre que l'on peut caractériser ainsi tous les graphes qui peuvent être tracés sur une surface donnée, en fonction d'un ensemble de mineurs exclus. La notion de mineur permet également d'exprimer simplement certains théorèmes ou conjectures, comme la conjecture de Hadwiger selon laquelle tout graphe ${\displaystyle G}$ dont le graphe complet à ${\displaystyle k}$ sommets n'est pas un mineur est colorable avec ${\displaystyle k-1}$ couleurs.

La théorie des mineurs de graphes est aussi liée au concept de décomposition arborescente.

• (en) László Lovász, « Graph Minor Theory », Bull. Amer. Math. Soc. (New Series), vol. 43, n^o 1,‎ 2005, p. 75–86 (lire en ligne) [PDF]
• (en) Neil Robertson et Paul Seymour, « Graph Minors. I. Excluding a forest », Journal of Combinatorial Theory, Series B, vol. 35, n^o 1,‎ 1983, p. 39–61 (DOI 10.1016/0095-8956(83)90079-5).
  Le premier des vingt-trois articles de la série Graph Minors, intitulé Mineurs : exclusion d'une forêt.

• Théorème de Robertson-Seymour
• Théorème du snark
• Théorème du séparateur planaire