Algorithme rho de Pollard

Soit ${\displaystyle n=pq}$ un nombre entier composé, où ${\displaystyle p}$ est un facteur non-trivial inconnu, que l'algorithme essaye de déterminer. On se place dans ${\displaystyle S=\mathbb {Z} /n\mathbb {Z} }$ ; autrement dit, on est dans ${\displaystyle \{0,\dots ,n-1\}}$ et les calculs s'effectuent modulo ${\displaystyle n}$.

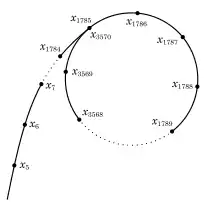
Fixons une fonction ${\displaystyle f:S\to S}$, par exemple ${\displaystyle f:x\mapsto x^{2}+1}$. La fonction devant être rapide à calculer et pseudo-aléatoire. On définit alors la suite ${\displaystyle (x_{n})}$ par ${\displaystyle x_{n+1}=f(x_{n})}$, où ${\displaystyle x_{0}\in S}$ est choisi de manière aléatoire. Comme la suite ${\displaystyle (x_{n})}$ prend un nombre fini de valeurs, elle finit par se répéter. C'est la raison du nom de l'algorithme : une représentation graphique de la suite cyclique ressemble à la lettre grecque ρ, voir figure ci-contre.

Considérons maintenant la suite des valeurs ${\displaystyle x_{n}{\text{ mod }}p}$. Comme ${\displaystyle p}$ est inconnu, cette suite ne peut pas être calculée explicitement. Nous savons qu'elle se répète également. A cause du paradoxe des anniversaires, sa période de répétition est souvent strictement plus petite que celui de la suite ${\displaystyle x_{n}}$. Si tel est le cas, il existe deux indices ${\displaystyle i<j}$ tels que ${\displaystyle x_{i}\equiv x_{j}{\pmod {p}}}$ mais ${\displaystyle x_{i}\not \equiv x_{j}{\pmod {n}}}$.

Alors ${\displaystyle p}$ divise ${\displaystyle \mathrm {pgcd} (x_{j}-x_{i},n)}$ mais ${\displaystyle \mathrm {pgcd} (x_{j}-x_{i},n)\neq n}$. Autrement dit, ${\displaystyle \mathrm {pgcd} (x_{j}-x_{i},n)}$ est un facteur non trivial de ${\displaystyle n}$.

Pour déterminer les indices ${\displaystyle i}$ et ${\displaystyle j}$, on utilise l'algorithme de Floyd pour rechercher un cycle. Il suffit alors de calculer ${\displaystyle \mathrm {pgcd} (x_{2k}-x_{k},n)}$ (pour ${\displaystyle k\geq 1}$) jusqu'à obtenir un facteur non trivial de ${\displaystyle n}$ ou bien obtenir le facteur ${\displaystyle n}$. En effet, celui-ci indique qu'on a ${\displaystyle x_{k}=x_{2k}}$, donc qu'on a terminé de parcourir le cycle des ${\displaystyle (x_{k})}$. On peut alors recommencer en changeant la valeur de ${\displaystyle x_{0}}$ ou la fonction ${\displaystyle g}$.

On donne ici le pseudo-code, comme dans [4].

entrée : un entier n composé, qui n'est pas une puissance d'un nombre premier
sortie : un facteur non trivial de n, ou alors une erreur
Pollard-Rho(n)    
    (a, b) := (2, 2)                 # dans [4], ils prennent x0 = 2
    répéter
           (a, b) = (f(a), f(f(b)))
           d := pgcd(a-b, n)
           si 1 < d < n
                    retourner d
           si d = n
                    erreur

En Python après avoir défini une fonction pgcd:

def rho_pollard(n):
    def f(x):
        return x*x+1
    x, y, d = 2, 2, 1
    while d==1:
        x = f(x) % n
        y = f(f(y)) % n
        print (x,y)
        d = pgcd(x-y, n)
    return d

Soit n = 8 051 et f(x) = x² + 1 mod 8 051. On prend x₀ = 2.

97 est un facteur non trivial de 8 051. Les autres valeurs de c peuvent donner le facteur 83 à la place de 97.

Considérons ${\displaystyle n}$ un nombre entier réel à factoriser à l'aide de l'algorithme. Soit ${\displaystyle p}$ un facteur premier de ${\displaystyle n}$, il est probable d'obtenir ce facteur ${\displaystyle p}$ après ${\displaystyle \Theta ({\sqrt {p}})}$ itérations de la boucle et nous pouvons donc estimer de manière heuristique à l'aide du paradoxe des anniversaires la complexité de algorithme à ${\displaystyle O({\sqrt[{4\,}]{n}})}$[5] mais une preuve plus rigoureuse reste à apporter[6]. L'algorithme est ainsi très rapide pour les nombres avec des petits facteurs. Par exemple, sur une station de travail à 733 MHz, une implémentation de l'algorithme rho, sans aucune optimisation, trouve le facteur 274 177 du sixième nombre de Fermat en une demi-seconde. Le sixième nombre de Fermat est 18 446 744 073 709 551 617 (20 chiffres décimaux). Néanmoins, pour un nombre semi-premier de même taille, la même station de travail prend environ 9 secondes pour trouver un facteur de 10 023 859 281 455 311 421 (le produit de 2 nombres premiers à 10 chiffres).

Pour f, nous choisissons un polynôme avec coefficients entiers. Les plus communs sont de la forme :

${\displaystyle f(x)=x^{2}+c,\quad c\notin \{0,-2\}.}$

Pour certains f, l'algorithme ne trouvera pas de facteur. Si pgcd(|x_a − x_b|, n) = n, l'algorithme échouera, parce que x_a = x_b, ce qui veut dire que la suite était bouclée et cela continuera tant que le travail précédent se répètera. En changeant c ou f, on peut augmenter la chance de succès. Cette situation d'échec peut survenir pour tous les nombres premiers, elle peut survenir pour certains nombres composés aussi.