MD5
Le MD5, pour Message Digest 5, est une fonction de hachage cryptographique qui permet d'obtenir l'empreinte numérique d'un fichier (on parle souvent de message). Il a été inventé par Ronald Rivest en 1991.

Si l'algorithme MD5 présente un intérêt historique important, il est aujourd'hui considéré comme dépassé et absolument impropre à toute utilisation en cryptographie ou en sécurité[1] - [2]. Il est toutefois encore utilisé pour vérifier l'intégrité d'un fichier après un téléchargement.
Historique
MD5 (Message Digest 5) est une fonction de hachage cryptographique qui calcule, à partir d'un fichier numérique, son empreinte numérique (en l'occurrence une séquence de 128 bits ou 32 caractères en notation hexadécimale) avec une probabilité très forte que deux fichiers différents donnent deux empreintes différentes.
En 1991, Ronald Rivest améliore l'architecture de MD4 pour contrer des attaques potentielles qui seront confirmées plus tard par les travaux de Hans Dobbertin.
Cinq ans plus tard, en 1996, une faille qualifiée de « grave » (possibilité de créer des collisions à la demande) est découverte et indique que MD5 devrait être mis de côté au profit de fonctions plus robustes comme SHA-1.
En 2004, une équipe chinoise découvre des collisions complètes. MD5 n'est donc plus considéré comme sûr au sens cryptographique. On suggère maintenant d'utiliser plutôt des algorithmes tels que SHA-256, RIPEMD-160 ou Whirlpool.
Cependant, la fonction MD5 reste encore largement utilisée comme outil de vérification lors des téléchargements et l'utilisateur peut valider l'intégrité de la version téléchargée grâce à l'empreinte. Ceci peut se faire avec un programme comme md5sum pour MD5 et sha1sum pour SHA-1.
Comme toute fonction de hachage cryptographique, MD5 peut aussi être utilisé pour calculer l'empreinte d'un mot de passe avec la présence d'un sel permettant de ralentir une attaque par force brute. Cela a été le système employé dans GNU/Linux. Ainsi, plutôt que de stocker les mots de passe dans un fichier, ce sont leurs empreintes MD5 qui étaient enregistrées (SHA-256, SHA-512 -par défaut- ou DES sont maintenant utilisés), de sorte que quelqu'un qui lirait ce fichier ne pourrait pas découvrir les mots de passe. La commande enable secret des commutateurs et routeurs Cisco utilisait le hachage MD5 (5 pour indiquer MD5) pour stocker le mot de passe du mode privilégié dans le fichier de configuration de l'équipement. Les dernières versions d'IOS intègrent le hachage SHA256 (4 pour indiquer SHA256)[3]. Cependant, il est recommandé aujourd'hui d'utiliser des fonctions de hachage destinées au stockage des mots passe telles que bcrypt, scrypt ou Argon2, car elles ont l'avantage d'être lentes, ce qui ralentit l'adversaire souhaitant attaquer les mots de passe.
Le programme John the ripper permet de casser (inverser la fonction pour) les MD5 triviaux par force brute. Il est incommode pour les clés longues, et ne fonctionne pas toujours si elles contiennent des caractères nationaux spécifiques (cela dépend en fait des dictionnaires utilisés).
Les rainbow tables (à accès direct, et qui font parfois plusieurs gigaoctets) permettent de les craquer souvent en moins d'une seconde. Ces tables utilisent des dictionnaires établis après plusieurs jours, mois ou années de calcul. Ceux-ci ne contiennent pas la totalité des clés MD5 possibles, ni ne sont destinés à un cassage par force brute (une empreinte comporte 128 bits, ce qui représente environ 400 sextillions () de combinaisons), mais permettent par examen de l'empreinte d'éliminer de très grandes classes de combinaisons à ne pas tester, ce qui accélère la recherche plusieurs milliards de fois. L'efficacité des tables arc-en-ciel diminue si l'empreinte est calculée avec un « sel ».
Exemple
Voici l'empreinte (appelée abusivement signature) obtenue sur une phrase :
- MD5("Et l’unique cordeau des trompettes marines") = 8747e564eb53cb2f1dcb9aae0779c2aa
En modifiant un caractère, cette empreinte change radicalement :
- MD5("Et l’unique cordeau des trompettes marinEs") = c802e1bd9b5f2b0d244bbc982f5082b3
Très concrètement, la vérification de l'empreinte ou somme de contrôle MD5 peut être réalisée de la façon suivante : lors du téléchargement d'un programme, on note la série de caractères nommée « Signature MD5 » indiquée sur la page de téléchargement. Quand ce téléchargement est terminé, on lance un utilitaire de calcul MD5 comme HashCalc, md5sums (Windows) ou md5sum (Linux), qui indique entre autres la somme de contrôle correspondant au fichier. Si les deux valeurs correspondent, on peut alors raisonnablement considérer que le fichier n'a pas été corrompu (volontairement ou non d'ailleurs). On constate plusieurs fragilités dans ce processus : la page d'origine a pu être modifiée, et l'utilitaire de calcul peut être adapté pour fournir la signature attendue. C'est pourquoi il faut impérativement utiliser un utilitaire provenant d'une source de confiance. Il est aussi possible d'utiliser une extension pour le navigateur Mozilla Firefox comme MD Hash tool[4] afin d'automatiser ce contrôle.
Cryptanalyse
À ses débuts, la fonction MD5 était considérée comme sûre, mais au cours du temps, des failles ont été découvertes dans son fonctionnement et durant l'été 2004, il a été cassé par des chercheurs chinois, Xiaoyun Wang, Dengguo Feng, Xuejia Lai (co-inventeur du célèbre algorithme de chiffrement IDEA) et Hongbo Yu. Leur attaque a permis de découvrir une collision complète (deux messages différents qui produisent la même empreinte) sans passer par une méthode de type recherche exhaustive[5].
Sur un système parallélisé, les calculs n'ont pris que quelques heures. Le MD5 n'est donc plus considéré comme sûr, mais l'algorithme développé par ces trois chercheurs concerne des collisions quelconques et ne permet pas de réaliser une collision sur une empreinte spécifique, c'est-à-dire réaliser un deuxième message, à partir de l'empreinte d'un premier message, qui produirait la même empreinte. Un projet de calcul distribué lancé en , MD5CRK (en), visait à découvrir une collision complète mais a été subitement arrêté après la découverte de l'équipe chinoise. La sécurité du MD5 n'étant plus garantie selon sa définition cryptographique, les spécialistes recommandent d'utiliser des fonctions de hachage plus récentes comme le SHA-256.
On sait maintenant générer des collisions MD5 en moins d'une minute lorsque les deux blocs en collisions sont « libres »[6]. On peut aussi générer une infinité de collisions avec un texte T à partir de deux messages M1 et M2 de même longueur qui sont en collision. Il suffit de concaténer M1 et M2 avec T, tel que T1 = M1 + T et T2 = M2 + T, afin d'obtenir une collision complète entre T1 et T2. On ne peut toutefois pas générer une signature particulière et la falsification de documents reste un exercice difficile.
Dès 2006, il est par exemple possible de créer des pages HTML aux contenus très différents et ayant pourtant le même MD5. La présence de métacodes de « bourrage » placés en commentaires, visibles seulement dans le source de la page web, trahit toutefois les pages modifiées pour usurper le MD5 d'une autre. La supercherie peut donc être levée si on examine les sources de la page en question.
En 2008, le logiciel BarsWF[7] utilise les ressources des instructions SSE2 et des processeurs massivement parallèles d'une carte graphique (CUDA) pour casser du MD5 en force brute à la vitesse annoncée de 350 millions de clés par seconde.
Algorithme
Notation
Préparation du message
MD5 travaille avec un message de taille variable et produit une empreinte de 128 bits. Le message est divisé en blocs de 512 bits, on applique un remplissage de manière à avoir un message dont la longueur est un multiple de 512. Le remplissage se présente comme suit :
- on ajoute un 1 à la fin du message ;
- on ajoute une séquence de '0' (le nombre de zéros dépend de la longueur du remplissage nécessaire) ;
- on écrit la taille du message, un entier codé sur 64 bits.
Ce remplissage est toujours appliqué, même si la longueur du message peut être divisée par 512. Cette méthode de padding est semblable à celle utilisée dans la plupart des algorithmes de message digest des familles MD (comme MD5 ou RIPEMD) ou SHA (SHA-1 ou SHA-512) mais différente de celle de l'algorithme Tiger qui utilise une convention dite Little endian d'ordonnancement des bits dans chaque octet.
La taille du message est codée en Little endian. Le message a maintenant une taille en bits multiple de 512, c'est-à-dire qu'il contient un multiple de 16 mots de 32 bits.
Constantes
MD5 utilise 64 valeurs constantes de mots de 32 bits, notés . ces nombres représentent des sinus d'entiers. Les valeurs suivantes sont exprimées en notation hexadécimale (base 16).
Ils peuvent être obtenus avec la formule .
| 0xd76aa478 | 0xe8c7b756 | 0x242070db | 0xc1bdceee | 0xf57c0faf | 0x4787c62a | 0xa8304613 | 0xfd469501 | |
| 0x698098d8 | 0x8b44f7af | 0xffff5bb1 | 0x895cd7be | 0x6b901122 | 0xfd987193 | 0xa679438e | 0x49b40821 | |
| 0xf61e2562 | 0xc040b340 | 0x265e5a51 | 0xe9b6c7aa | 0xd62f105d | 0x02441453 | 0xd8a1e681 | 0xe7d3fbc8 | |
| 0x21e1cde6 | 0xc33707d6 | 0xf4d50d87 | 0x455a14ed | 0xa9e3e905 | 0xfcefa3f8 | 0x676f02d9 | 0x8d2a4c8a | |
| 0xfffa3942 | 0x8771f681 | 0x6d9d6122 | 0xfde5380c | 0xa4beea44 | 0x4bdecfa9 | 0xf6bb4b60 | 0xbebfbc70 | |
| 0x289b7ec6 | 0xeaa127fa | 0xd4ef3085 | 0x04881d05 | 0xd9d4d039 | 0xe6db99e5 | 0x1fa27cf8 | 0xc4ac5665 | |
| 0xf4292244 | 0x432aff97 | 0xab9423a7 | 0xfc93a039 | 0x655b59c3 | 0x8f0ccc92 | 0xffeff47d | 0x85845dd1 | |
| 0x6fa87e4f | 0xfe2ce6e0 | 0xa3014314 | 0x4e0811a1 | 0xf7537e82 | 0xbd3af235 | 0x2ad7d2bb | 0xeb86d391 |
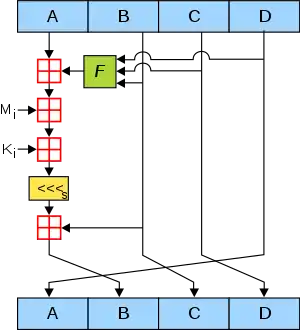
Boucle principale
L'algorithme principal travaille avec un état sur 128 bits. Il est lui-même divisé en 4 mots de 32 bits (en informatique, on utilise le terme "mot" pour désigner une valeur de 32 bits ou "word" en anglais) : A, B, C et D. Ils sont initialisés au début avec des constantes. L'algorithme utilise ensuite les blocs provenant du message à hacher, ces blocs vont modifier l'état interne. Les opérations sur un bloc se décomposent en quatre rondes (étapes), elles-mêmes subdivisées en 16 opérations similaires basées sur une fonction non linéaire F qui varie selon la ronde, une addition et une rotation vers la gauche. Les quatre fonctions non linéaires disponibles sont :
- ;
- ;
- ;
- .
représente les opérateurs booléens XOR, ET, OU et NON, respectivement.
Pseudo-code
MD5 peut s'écrire sous cette forme en pseudo-code.
//Note : Toutes les variables sont sur 32 bits //Définir r comme suit : var entier[64] r, k r[ 0..15] := {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22} r[16..31] := {5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20} r[32..47] := {4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23} r[48..63] := {6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21} //MD5 utilise des sinus d'entiers pour ses constantes : pour i de 0 à 63 faire k[i] := floor(abs(sin(i + 1)) × 2^32) fin pour //Préparation des variables : var entier h0 := 0x67452301 var entier h1 := 0xEFCDAB89 var entier h2 := 0x98BADCFE var entier h3 := 0x10325476 //Préparation du message (padding) : ajouter le bit "1" au message ajouter le bit "0" jusqu'à ce que la taille du message en bits soit égale à 448 (mod 512) ajouter la taille du message initial(avant le padding) codée en 64-bit little-endian au message //Découpage en blocs de 512 bits : pour chaque bloc de 512 bits du message subdiviser en 16 mots de 32 bits en little-endian w[i], 0 ≤ i ≤ 15 //initialiser les valeurs de hachage : var entier a := h0 var entier b := h1 var entier c := h2 var entier d := h3 //Boucle principale : pour i de 0 à 63 faire si 0 ≤ i ≤ 15 alors f := (b et c) ou ((non b) et d) g := i sinon si 16 ≤ i ≤ 31 alors f := (d et b) ou ((non d) et c) g := (5×i + 1) mod 16 sinon si 32 ≤ i ≤ 47 alors f := b xor c xor d g := (3×i + 5) mod 16 sinon si 48 ≤ i ≤ 63 alors f := c xor (b ou (non d)) g := (7×i) mod 16 fin si var entier temp := d d := c c := b b := leftrotate((a + f + k[i] + w[g]), r[i]) + b a := temp fin pour //ajouter le résultat au bloc précédent : h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d fin pour var entier empreinte := h0 concaténer h1 concaténer h2 concaténer h3 //(en little-endian)
Notes et références
- Dougherty Chad R, « Vulnerability Note VU#836068 MD5 vulnerable to collision attacks », sur Vulnerability notes database, CERT Carnegie Mellon University Software Engineering Institute, (consulté le )
- (en) Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, « Creating a rogue CA certificate », .
- Wendell Odom (trad. de l'anglais), Préparation à la certification CCNA ICND1 et CCENT : Guide de la préparation officiel Deuxième édition, Paris, PEARSON, , CCIE 1624 éd., 662 p. (ISBN 978-2-7440-7285-7), chap. 9 (« Configuration des commutateurs Ethernet »), p. 265à voir en première ligne de la page.
- (en) « mozdev.org - mdhashtool: installation ».
- (en) « Musings on the Wang et al. MD5 Collision » [PDF].
- Vlastimil Klima, « Tunnels in Hash Functions: MD5 Collisions Within a Minute, Cryptology ePrint Archive Report 2006/105 », .
- (en) « World Fastest MD5 cracker BarsWF ».
Annexes
Articles connexes
Liens externes
- (en) « RFC 1321 qui détaille l'algorithme »
- « Fonction de décryptage MD5 »
- (en) Ondrej Mikle, « Practical Attacks on Digital Signatures Using MD5 Message Digest »
- (en) Vlastimil Klíma, « Finding MD5 collisions - A toy for notebook » [PDF]
- (en) P. Hawkes et al., « Musings on the Wang et al. - MD5 Collision » [PDF]
- (en) « Générateur de Hash MD5 - MD5 HASH Generator »















