SHA-1
SHA-1 (Secure Hash Algorithm, prononcé /ʃa.œ̃/[1]) est une fonction de hachage cryptographique conçue par la National Security Agency des États-Unis (NSA), et publiée par le gouvernement des États-Unis comme un standard fédéral de traitement de l'information (Federal Information Processing Standard du National Institute of Standards and Technology (NIST)). Elle produit un résultat (appelé « hash » ou condensat) de 160 bits (20 octets), habituellement représenté par un nombre hexadécimal de 40 caractères.
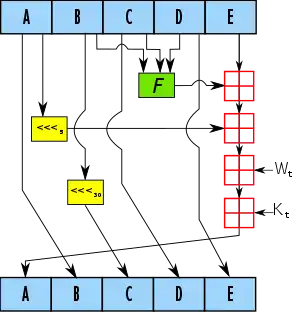
A, B, C, D, E sont des mots de 32 bits ;
<<<n désigne une rotation des bits par décalage de n bits vers la gauche ;
F est une fonction (non linéaire sur le corps F2 des booléens) qui dépend du numéro de tour t ;
⊞ est l'addition modulo 232 (l'addition des entiers machines non signés de 32 bits), qui est non linéaire sur F2 ;
Kt est une constante (32 bits) qui dépend du numéro de tour t ;
Wt est un mot de 32 bits qui dépend du numéro de tour t ; il est obtenu par une procédure d'expansion à partir du bloc de donnée (512 bits) dont le traitement est en cours.
SHA-1 n'est plus considéré comme sûr contre des adversaires disposant de moyens importants. En 2005, des cryptanalystes ont découvert des attaques sur SHA-1, suggérant que l'algorithme pourrait ne plus être suffisamment sûr pour continuer à l'utiliser dans le futur[2]. Depuis 2010, de nombreuses organisations ont recommandé son remplacement par SHA-2 ou SHA-3[3] - [4] - [5]. Microsoft[6], Google[7] et Mozilla[8] - [9] - [10] ont annoncé que leurs navigateurs respectifs cesseraient d'accepter les certificats SHA-1 au plus tard en 2017.
Origine : SHA-0 et SHA-1
Le SHA-1 est le successeur du SHA-0 qui a été rapidement mis de côté par le NIST pour des raisons de sécurité insuffisante. Le SHA-0 était légitimement soupçonné de contenir des failles qui permettraient d'aboutir rapidement à des collisions (deux documents différents qui génèrent le même condensat). Face à la controverse soulevée par le fonctionnement du SHA-0 et certains constats que l'on attribue à la NSA, le SHA-0 s'est vu modifié peu après sa sortie (1993) et complexifié pour devenir le SHA-1 (1995). Une collision complète sur le SHA-0 a été découverte par Antoine Joux et al. en . En 2005, la cryptanalyste Xiaoyun Wang et ses co-auteurs Yiqun Lisa Yin et Hongbo Yu annoncent une attaque théorique pour la recherche de collisions pour SHA-1 qui est plus efficace que l'attaque des anniversaires (l'attaque générique de référence)[11]. L'attaque complète sera publiée à Crypto 2015[12]. Le NIST pour sa part recommande de passer sur un algorithme SHA-2 ou SHA-3 quand c'est possible. Depuis 2013, Microsoft a déclaré l’obsolescence du SHA-1[13] et en 2014. L'ANSSI déconseille son utilisation dans la seconde version de son Référentiel Général de Sécurité (RGS)[14] d'application au . Enfin, Google annonce que ses versions de Chrome n'accepteront plus, de façon graduelle, le SHA-1 jusqu'à le refuser pour les certificats expirant après le [15].
En Google et le Centrum voor Wiskunde en Informatica annoncent une attaque effective et la première collision sur SHA-1[16].
Exemples
Voici la signature obtenue sur une phrase (codée en utf8) : SHA1("Wikipédia, l'encyclopédie libre et gratuite") = 6153A6FA0E4880D9B8D0BE4720F78E895265D0A9.
En modifiant un caractère, la signature change radicalement : SHA1("Wikipédia, l'encyclopédie libre et gratuitE") = 11F453355B28E1158D4E516A2D3EDF96B3450406.
Le SHA-1 est un excellent générateur de nombres pseudo-aléatoires (comme beaucoup de fonctions de hachage) et il passe avec succès tous les tests statistiques.
Fonctionnement du SHA-1
Le SHA-1 prend un message d'un maximum de 264 bits en entrée. Son fonctionnement est similaire à celui du MD4 ou MD5 de Ronald Rivest. Quatre fonctions booléennes sont définies, elles prennent 3 mots de 32 bits en entrée et calculent un mot de 32 bits. Une fonction spécifique de rotation est également disponible, elle permet de déplacer les bits vers la gauche (le mouvement est circulaire et les bits reviennent à droite). Une de ces rotations n'était pas présente dans le SHA-0, elle permet de casser certaines caractéristiques linéaires dans la structure. Cela permet d'éviter une attaque sur les bits neutres décrite par Eli Biham, technique reprise pour calculer la collision complète sur SHA-0 (Antoine Joux et al.).
Le SHA-1 commence par ajouter à la fin du message un bit à 1 suivi d'une série de bits à 0, puis la longueur du message initial (en bits) codée sur 64 bits. La série de 0 a une longueur telle que la séquence ainsi prolongée a une longueur multiple de 512 bits. L'algorithme travaille ensuite successivement sur des blocs de 512 bits.
Pour chaque bloc l'algorithme calcule 80 tours (ou rondes, « rounds » en anglais) successifs et applique une série de transformations sur l'entrée. La première étape consiste à calculer 80 valeurs sur 32 bits. Les 16 premières valeurs sont obtenues directement à partir du bloc « message » en entrée. Les 64 autres sont calculées successivement. Le SHA-1 les obtient grâce à une rotation (absente dans SHA-0) qui est appliquée sur le résultat d'un XOR, il utilise pour cela 4 mots obtenus dans les itérations précédentes. On définit ensuite cinq variables qui sont initialisées avec des constantes (spécifiées par le standard), le SHA-1 utilise encore 4 autres constantes dans ses calculs. Si un bloc de 512 bits a déjà été calculé auparavant, les variables sont initialisées avec les valeurs obtenues à la fin du calcul sur le bloc précédent.
Il s'ensuit 80 tours qui alternent des rotations, des additions entre les variables et les constantes. Selon le numéro du tour, le SHA-1 utilise une des quatre fonctions booléennes. L'une de ces fonctions est appliquée sur 3 des 5 variables disponibles. Les variables sont mises à jour pour le tour suivant grâce à des permutations et une rotation. En résumé, le SHA-1 change sa méthode de calcul tous les 20 tours et utilise les sorties des tours précédents.
À la fin des 80 tours, on additionne le résultat avec le vecteur initial. Lorsque tous les blocs ont été traités, les cinq variables concaténées (5 × 32 = 160 bits) représentent la signature.
Caractéristiques
Les caractéristiques de SHA-1 sont les suivantes :
- taille du message : 264 bits maximum
- taille des blocs : 512 bits
- taille des mots : 32 bits
- taille du condensé : 160 bits
- niveau de sécurité : collision en 263 opérations.
L’attaque générique des anniversaires permet de trouver une collision en 280 opérations, ce qui est donc la sécurité attendue pour une telle fonction de hachage. Mais dans le cas de SHA-1, il existe une attaque théorique en 269 connue depuis 2005[17], qui a été améliorée en une attaque en 263 opérations. Ces attaques, bien que théoriques, ouvrent la possibilité que de réelles collisions soient découvertes (ce qui est également une question de temps et de moyens).
Détails de l'algorithme
Les spécifications de SHA-1 sont décrites pour la première fois en avril 1995 dans le document officiel du NIST FIPS 180-1 pour un standard de fonction de hachage cryptographique[18]. Elles sont reprises dans les versions successives de ce document, FIPS-180-2, FIPS-180-3 et FIPS-180-4[19].
L'algorithme SHA-1 transforme un message de longueur inférieure à 264 bits en un haché, ou condensé de ce message, qui est de longueur 160 bits. Il adopte la construction de Merkle-Damgård : schéma itératif à partir d'une fonction de compression dont l'entrée est de taille fixe, et ajout en fin de message de sa longueur (renforcement de Merkle-Damgård, (en)Merkle-Damgård strengthening) ce qui permet de réduire la résistance aux collisions de la fonction de hachage à celle de la fonction de compression.
Cet algorithme peut être découpé en deux phases : le prétraitement et le calcul du condensé.
- Le prétraitement implique
- de compléter le message par des informations le rendant compatible avec l'algorithme SHA-1 (remplissage)
- son analyse pour le découper en blocs de 512 bits
- l'initialisation de variables de travail
- Le calcul du condensé génère un tableau à partir du message complété, puis le transforme via l'utilisation de fonctions, de constantes, d'opérations binaires détaillées plus loin. L'ensemble effectué de manière itérative permet de générer des séries de valeurs de hachage à chaque tour. Le condensé final est le dernier état de ces valeurs de hachage.
Paramètres
- a, b, c, d, e = variables de travail (en l'occurrence des mots de w bits), utilisées dans le calcul des hachés.
- = la valeur de hachage n°i. est la valeur initiale du hachage. est la dernière valeur de hachage.
- = le mot (w bits) n°j de la valeur de hachage n°i, où est le mot de poids le plus fort (à gauche) de la valeur de hachage i.
- = constantes itératives selon la valeur de t, utilisées dans le calcul de hachage
- k = nombre de 0 ajoutés au message lors du prétraitement (complément)
- l = longueur du message M, en bits
- m = nombre de bits contenus dans un bloc, soit 512 bits
- M = message à traiter
- = bloc n°i (m bits), du message M
- = mot (w bits) n°j, du bloc (m bits) n°i, du message M
- n = nombre de bits de décalage ou de rotation à appliquer au mot quand associé à une fonction binaire
- N = nombre de blocs de m bits contenus dans le message M après complément
- T = variable temporaire, mot de w bits, utilisée dans le calcul de condensé
- w = nombre de bits contenus dans un mot, soit 32 bits.
- = le mot n°t du tableau déduit du message
Symboles
La notation hexadécimale utilisée ici sera: (exemple : )
- = opération binaire AND
- = opération binaire OR
- = opération binaire XOR
- = complément binaire
- = addition modulo
- = décalage binaire à gauche, où s'obtient en supprimant les n bits de gauche de x et ajoutant n zéros à droite.
- = décalage binaire à droite, où s'obtient en supprimant les n bits de droite de x et ajoutant n zéros à gauche.
Opérations sur les mots
Elles utilisent les conventions suivantes :
- opérations binaires bit à bit (cf. symboles)
- addition modulo , soit
L'opération est définie comme suit. Soient deux mots représentant les nombres entiers , tels que et , on a le résultat de l'addition modulo de .
. On convertit en un mot , et on définit alors - l'opération de rotation binaire par la gauche , où x est un mot de 32 bits et , est définie par:
Fonctions
Cette section décrit les fonctions utilisées lors du calcul des valeurs de hachage. SHA-1 utilise une succession de fonctions logiques . Chaque fonction , où , travaille sur trois variables entières de 32 bits et retourne un entier de 32 bits :
définie par une des trois fonctions binaires classiques suivantes, où
est la fonction binaire (plusieurs formules équivalentes ci-dessus) de choix entre les bits correspondants des deux premières variables, selon la valeur du bit correspondant de la troisième variable,
est la fonction binaire (plusieurs formules équivalentes ci-dessus, ainsi que d'autres car elle est commutative sur ses 3 variables) indiquant si la majorité (au moins deux) des trois bits correspondants des trois variables sont à 1, et
est la fonction binaire (commutative sur toutes ses variables) d'union exclusive ou parité des trois variables.
Constantes
SHA-1 utilise quatre valeurs réparties dans les 80 constantes , d'après la règle
Prétraitement
Cette opération se déroule en trois étapes : compléter le message M, découper le résultat en blocs, et initialiser les valeurs de hachage
Complément de M
Il s'agit ici d'ajouter des informations à M pour qu'il soit d'une taille multiple de 512 bits.
pour ce faire, l'on ajoute un bit "1" à la fin du message M, puis k zéros, où k est la plus petite solution non négative de l'équation: l + 1 + k = 448 mod 512, avec l = taille de M en bits.
On ajoute alors un bloc de 64 bits correspondant à la représentation binaire de l.
Exemples :
- M = "abc", l = 8 x 3 = 24, k = 448 - (l + 1) = 448 - (24 + 1) = 423
On ajoute "1", puis quatre cent vingt trois "0", puis 64 bits finissant par "011000" (pour 24) à M.
On obtient alors un message complété à 512 bits. - M quelconque tel que l = 500 bits, k = 448 - (l + 1) = 448 - (500 + 1) = -53
Comme k ne peut pas être négatif, on lui ajoute 512 en prenant en compte le modulo de l'équation, pour obtenir
On ajoute "1", puis quatre cent cinquante neuf "0", puis 64 bits finissant par "111110100" (pour 500) à M.
On obtient alors un message complété à 512 bits.
Découpage en blocs
Le message complété est découpé en N blocs de 512 bits, notés . Chaque bloc de 512 bits est ensuite découpé en 16 mots de 32 bits, notés .
Initialisation
Le vecteur initial est défini comme suit :
Calcul du condensé (haché)
Pour ce traitement on utilisera :
- la fonction d'expansion d'un bloc de 16 mots du message en un bloc intermédiaire de 80 mots :
- la fonction suivante de compression d'un bloc intermédiaire de 80 mots sur un vecteur de 5 mots :
- où notée ci-après est la fonction binaire, décrite plus haut.
- cinq variables contenant les valeurs de hachage, notées et initialisées précédemment en .
Ces variables contiendront itérativement de nouvelles valeurs de hachage, , pour finalement contenir le condensé de M, dans .
On traite successivement les blocs de M selon les étapes suivantes, pour :
- On étend un bloc de 16 mots du message en un bloc temporaire de 80 mots où , selon
- On initialise un vecteur temporaire avec les valeurs de hachage du tour précédent :
- On réduit le bloc temporaire sur ce vecteur temporaire :
- où notée ci-après est la fonction logique, décrite plus haut.
- On combine le vecteur obtenu avec le condensé intermédiaire par une simple addition :
Après répétition des quatre étapes ci-dessus pour les N blocs du message M, le condensé de 160 bits de M est obtenu par concaténation des valeurs
Remarque : Il existe d'autres méthodes de calcul du condensé SHA-1 donnant des résultats identiques.
- On doit noter notamment que la rotation de 30 bits vers la gauche calculée sur 32 bits est trivialement équivalente à une rotation de 2 bits vers la droite .
- Comme le montrent Laurent et Peyrin dans leur article de 2019, les opérations de chacune des 80 boucles de l'étape 3 sont également réductibles, de façon équivalente, à une seule opération
- où les 5 variables sont en fait parties d'un unique registre d'état de 160 bits, dont on ne doit mémoriser à chaque boucle que les 4 valeurs précédentes
- Cela ne nécessite que de connaitre les valeurs d'initialisation des 3 « valeurs précédentes » associées à la valeur initiale du registre pour les 3 première boucles, ce qui est possible car les valeurs initiales (de l'étape 2) sont inversibles pour la fonction sur seulement 3 étapes, cette même fonction étant utilisée sans changement pour les 20 premières boucles dont les 3 premières, et toutes les fonctions définies à l'origine sur 32 bits sont extensibles sans changement à 160 bits).
- D'autre part, les rotations de cette dernière formule (réduite à une opération) portent sur des valeurs de 160 bits (et non 32 bits), de sorte qu'alors .
- La fonction de compression obtenue par ces 80 boucles est donc une composition récursive de fonctions à une seule variable de 160 bits (portant sur l'expansion triviale et inversible à 160 bits , à l'étape 1, d'un bloc de 32 bits extrait du message en clair), terminée par l'addition de la valeur de hachage intermédiaire du message jusqu'au bloc précédent (ou la valeur initiale constante de la fonction de hachage) :
- Noter que dans cette définition, les fonctions initialement définies sur 32 bits sont modifiées pour être étendues à 160 bits en utilisant la formule à une seule opération, où viennent s'ajouter les rotations sur 5 bits vers la gauche ou 2 bits vers la droite des valeurs précédentes de et les additions de constantes .
- La résistance aux collisions de SHA-1 est liée directement à la non-inversibilité (conjecturée) de la fonction composée obtenue , puisque la fonction d'expansion des messages est trivialement inversible.
Attaques
Une attaque brute basée sur le paradoxe des anniversaires permet de trouver une collision complète sur une clé SHA-1 complète (sur 160 bits) avec un nombre d'opérations de l'ordre de .
En 2005, Rijmen et Oswald ont publié une attaque sur une version simplifiée du SHA-1 (53 tours), leur attaque permet de trouver une collision avec moins de opérations.
En , Bruce Schneier a fait état d'une attaque sur la version complète du SHA-1 par l'équipe chinoise de Wang, Yin et Yu. Leur méthode permet de trouver :
- une collision dans le SHA-1 complet de 128 bits avec opérations au lieu de par l’attaque des anniversaires
- une collision dans le SHA-0 complet avec seulement opérations
- une collision dans une version simplifiée du SHA-1 (58 tours) avec opérations
La description de l'attaque a été publiée en .
Le , une amélioration de l'attaque a été annoncée par Wang et al. à la conférence CRYPTO 2005, la complexité passe ainsi de 269 à 263, soit une division par 64 de la complexité originale.
Lors de l'Eurocrypt 2009 (avril), une amélioration[20] de l'attaque aurait permis de réduire à nouveau sa complexité jusqu'à atteindre . Toutefois, ces résultats furent démentis et l'article[21] fut retiré[22] à la suite de la découverte d'une erreur dans l'évaluation de cette complexité.
Une équipe composée de chercheurs de chez Google et du CWI (Centrum Wiskunde et Informatica) ont annoncé le qu'ils avaient réussi à obtenir une collision entre deux documents[23] - [24].
Une équipe composée de chercheurs universitaires (Gaëtan Leurent de l'Inria en France et son collègue Thomas Peyrin de l'Université de Nanyang à Singapour) a annoncé en début avoir mis au point une attaque sur la version complète de SHA-1 (80 tours) permettant d'obtenir pour n'importe quelle valeur de hachage une collision sur des préfixes choisis en un nombre d'opérations situé entre et [25], ce qui réduit le coût d'obtention de collisions à moins de 150 000 $, à la portée d'une organisation de moyenne taille (ou de bandes organisées) et plus seulement de grandes organisations ou de gouvernements, basée sur une analyse différentielle multi-bloc (et non un bloc unique avec les tentatives précédentes), ce qui permet d'en améliorer l'efficacité en réduisant l'espace de recherche de façon incrémentielle. En , ces mêmes chercheurs ont annoncé avoir amélioré leur attaque et pouvoir obtenir une collision en opérations, pour un coût de 45k$[26]. Les investigations continuent pour déterminer le coût minimum de ce type d'attaque qui pourrait en pratique s'avérer même inférieur (des attaques similaires sont démontrées également sur d'autres algorithmes de hachage similaires, y compris MD5 qui était déjà connu pour être cassé mais qui le devient encore plus facilement). Toutefois l'attaque annoncée ne concerne pas encore les empreintes de messages (ou signatures) HMAC basées sur SHA-1[27] - [25]. Un code libre de démonstration et des données d'analyse seront bientôt mis en ligne sur GitHub afin d'évaluer correctement son impact notamment dans la sécurité de protocoles Internet comme TLS (utilisé notamment par HTTPS) et des certificats de serveurs, avec la possibilité alors de créer à bas coût une autorité de certification (CA) malveillante, notamment pour créer des failles de contournement de la sécurité de sites Internet (dont 5 % des plus connus et les plus visités utilisent encore en des certificats basés sur SHA-1, plusieurs années après la fin de leur recommandation, y compris encore Microsoft pour certains de ses services connectés comme Skype) ainsi que l'utilisabilité de la méthode pour casser d'autres algorithmes de hachages connus qui restent recommandés (dont RIPEMD-160, SHA-2 et SHA-3) et d'autres qui ne le sont pas encore.
Conséquences
Même si un gain de 217 opérations permettait de diviser le temps de recherche par un facteur de 131 072, l'attaque de 2009 avec ses 263 opérations était à la limite de ce qui était réalisable. Adi Shamir a toutefois laissé entendre que l'attaque pouvait probablement être abordée via un calcul distribué à l'échelle planétaire. Mais maintenant (en avec la méthode publiée par Leurent et Peyrin) avec un gain d'au moins 233 opérations (soit un facteur d'accélération voisin de dix milliards), une telle attaque est tout à fait réalisable de façon pratique avec des moyens facilement accessibles, d'autant plus qu'en 10 ans la performance des systèmes s'est considérablement accrue, avec en plus l'arrivée massive et à bas coût sur le marché mondial des GPU (ainsi qu'avec la multiplication des offres peu onéreuses d'hébergement d'applications privées sur le « cloud » permettant de les utiliser), capables de réaliser localement des calculs massivement parallèles et de façon discrète, sans faire nécessairement appel à des ressources externes distribuées (également détournées de façon illégale et aujourd'hui à très grande échelle) accessibles sur un réseau planétaire où une telle mise en œuvre pourrait être détectée assez facilement.
La règle veut qu'une attaque plus rapide que les attaques génériques (celle des anniversaires en l'occurrence) rende l'algorithme non sûr du point de vue cryptographique. De plus, la structure de SHA-1 reste assez proche de celle de MD5 (qui est déconseillé pour les nouvelles applications) pour lequel on a trouvé effectivement des collisions. Depuis l'annonce de l'attaque de Wang et al., SHA-1 a tendance à être retiré progressivement, au moins de certaines applications cryptographiques, essentiellement au profit de SHA-256 (d'autres fonctions de hachage sont également utilisées comme Whirlpool, Tiger, RIPEMD-160, et d'autres plus récentes comme ChaCha20, Curve25519, NTRU, ainsi que BLAKE2b ou BLAKE2s qui sont suggérés en pour les empreintes de mots de passe et pour la sécurisation des échanges de clés de chiffrement, en remplacement de SHA-1 et même de SHA-2 ou SHA-3). SHA-1 reste malheureusement encore largement utilisé, d'autant que la sécurité de certaines applications repose sur la résistance à la recherche de préimage (ce qui n'est plus le cas depuis si cette recherche est techniquement réalisable), et non sur la seule résistance aux collisions[17].
Vu les faiblesses constatées sur SHA-1, et la conception de SHA-2 qui est voisine, une compétition a été organisée par la NIST, afin de trouver un nouveau standard de hachage (SHA-3) comme cela fut le cas il y a quelques années pour la cryptographie symétrique avec AES. Toutefois les révélations d'Edouard Snowden concernant la manipulation par la NSA des constantes utilisées dans des algorithmes de sécurité standardisés par le NIST (y compris dans les algorithmes de chiffrement récents, et dans des algorithmes de génération de nombres pseudo-aléatoires basés sur les courbes elliptiques nécessaires à la production des clés de chiffrement) ont levé le doute sur la réelle sécurité des fonctions de hachage de la famille SHA : ainsi concernant SHA-1, les constantes d'initialisation n'obéissent de façon évidente à aucun critère cryptographique satisfaisant et ont un intérêt seulement mnémonique, elles pourraient ainsi constituer des portes dérobées volontairement introduites ou laissées par la NSA pour faciliter la découverte de collisions avec les moyens techniques dont disposait alors la NSA au moment de sa standardisation et sa publication par le NIST en 1995.
L'attaque produite par Wang et al. ne concerne que des collisions quelconques (tout comme leur fameuse collision complète sur le MD5). C’est-à-dire que l'on peut trouver deux messages au contenu aléatoire qui produisent la même signature. En revanche, à partir d'une signature donnée, il était considéré comme impossible (jusqu'en ) de forger un second message qui conduise à la même valeur, à condition d'utiliser un système d'authentification de messages (tel que HMAC) en complément de la fonction de hachage nécessaire à ce système. Or, c'est ce type d'attaque qui pourrait mettre en péril les applications comme PGP et l'authenticité des données.
Le SHA-1 en mode chiffrement
Les primitives des fonctions de hachage cryptographiques sont assez proches de celles des chiffrements symétriques. SHA-1, a été adaptée par Helena Handschuh et David Naccache pour obtenir un chiffrement par bloc appelé SHACAL.
Notes et références
E.A.Grechnikov,Collisions for 72-step and 73-step SHA-1: Improvements in the Method of Characteristics, (http://eprint.iacr.org/2010/413)
- Qu'est-ce qu'un certificat de signature de code ?, GoDaddy Canada La scène se produit à 54 s.
- (en) Schneier, Bruce, « Schneier on Security: Cryptanalysis of SHA-1 »,
- (en) « NIST.gov - Computer Security Division - Computer Security Resource Center »
- (en) Marc Stevens1, Pierre Karpman et Thomas Peyrin, « The SHAppening: freestart collisions for SHA-1 » (consulté le )
- (en) Bruce Schneier, « SHA-1 Freestart Collision », Schneier on Security,
- (en) « Windows Enforcement of Authenticode Code Signing and Timestamping », Microsoft, (consulté le )
- (en) « Intent to Deprecate: SHA-1 certificates », Google, (consulté le )
- (en) « Bug 942515 - stop accepting SHA-1-based SSL certificates with notBefore >= 2014-03-01 and notAfter >= 2017-01-01, or any SHA-1-based SSL certificates after 2017-01-01 », Mozilla (consulté le )
- (en) « CA:Problematic Practices - MozillaWiki », Mozilla (consulté le )
- (en) « Phasing Out Certificates with SHA-1 based Signature Algorithms | Mozilla Security Blog », Mozilla, (consulté le )
- « Cryptanalysis of SHA-1 - Schneier on Security », sur www.schneier.com (consulté le )
- « Finding Collisions in the Full SHA-1 », sur www.iacr.org (consulté le )
- « SHA1 Deprecation Policy - Windows PKI blog - Site Home - TechNet Blogs », sur blogs.technet.com (consulté le )
- ANSSI, « Liste des documents constitutifs du RGS v.2.0 », ANSSI, (lire en ligne, consulté le )
- « Google Groupes », sur groups.google.com (consulté le )
- (en) « Announcing the first SHA1 collision », sur Google Online Security Blog (consulté le ).
- RFC 6194
- FIPS 180-1, Federal Information Processing Standards Publication 180-1 Announcing the Standard for Secure Hash Standard, 17 avril 1995 lire en ligne
- voir page (en)Secure Hashing du NIST. En plus de SHA-1, le standard inclut les algorithmes de la famille SHA-2 à partir de la version (en)FIPS-180-2[PDF] (août 2002), avec de nouvelles variantes pour SHA-2 dans les versions successives (en)FIPS-180-3[PDF] (octobre 2008) et (en)FIPS-180-4[PDF] (mars 2012).
- http://eurocrypt2009rump.cr.yp.to/837a0a8086fa6ca714249409ddfae43d.pdf
- http://www.ictlex.net/wp-content/iacrhash.pdf
- (en) « Cryptology ePrint Archive : Report 2009/259 - Differential Path for SHA-1 with complexity $O(2^{52})$ », sur iacr.org (consulté le ).
- Julien Cadot, « SHAttered : Google a cassé la méthode de chiffrement SHA-1 », sur numerama, (consulté le )
- (en) site montrant deux documents ayant la même signature et explicant que SHA-1 est cassé
- (en) Gaëtan Leurent et Thomas Peyrin, « From Collisions to Chosen-Prefix Collisions - Application to Full SHA-1. » [PDF], sur IACR.org, (consulté le ), pour EUROCRYPT 2019, paru dans Advances in Cryptology, pp. 5247-555 (DOI: 10.1007/978-3-030-17659-4_18).
- (en) G. Leurent, « SHA-1 is a Shambles - First Chosen-Prefix Collision on SHA-1 and Application to the PGP Web of Trust », Usenix, (lire en ligne)
- (en) Catalin Cimpanu, « SHA-1 collision attacks are now actually practical and a looming danger », sur ZDNet, (consulté le ).
Voir aussi
Sources
- Cet article est partiellement ou en totalité issu de l'article intitulé « Spécifications SHA-1 » (voir la liste des auteurs).
Articles connexes
- Secure Hash Algorithm pour les autres algorithmes de cette famille
Liens externes
- (fr) Un calculateur de hash en SHA-1
- (en) SHA1 dictionary attack
- (en) Vidéo de CRYPTO 2005, avec la présentation de l'attaque améliorée par Adi Shamir
- (en) Slides d'Adi Shamir à CRYPTO 2005[PDF]
- (en) A New Statistical Testing for Symmetric Ciphers and Hash Functions, test statistique de Eric Filiol
- (en) SHACAL[PDF], description de SHA-1 en mode chiffrement (SHACAL)
- (en) RFC 3174, US Secure Hash Algorithm 1 (SHA1)
- (en) SHA-1 collisions now 252, L'attaque sur SHA-1 présentée à Eurocrypt 2009.




















































































