SHA-3

Keccak est une fonction éponge dont nous allons décrire la transformation, appelée f dans la terminologie de la construction de l’éponge. Cette transformation est une permutation valable en choisissant un mot d’une taille qui soit une puissance de deux w = 2^ℓ. Dans le cas de Keccak les mots sont de 64-bits, soit ℓ=6.

L’état interne de cette fonction sera vu comme une matrice de dimension 5×5×w. ${\displaystyle a[i][j][k]}$ sera le bit ${\displaystyle (i*5+j)*w+k}$ de l’entrée. Le calcul des indices est effectué modulo 5 pour les deux premières dimensions, et modulo w pour la troisième.

La fonction f de Keccak est une permutation qui consiste en 12+2ℓ itérations (soit 24) de cinq sous routines assez simples :

La routine θ

Calculer la parité des 5×w colonnes (de 5 bits) de l’état, puis calculer le ou exclusif entre deux colonnes voisines. ${\displaystyle a[i][j][k]\leftarrow a[i][j][k]\oplus parite(a[0..4][j-1][k])\oplus parite(a[0..4][j+1][k-1])}$

La routine ρ

Décaler circulairement les 25 mots d’un nombre triangulaire (0, 1, 3, 6, 10, 15, …). ${\displaystyle a[0][0]}$ n’est pas décalé, et :

pour chaque 0 ≤ t < 24 :${\displaystyle {\begin{pmatrix}i\\j\end{pmatrix}}\leftarrow {\begin{pmatrix}3&2\\1&0\end{pmatrix}}^{t}{\begin{pmatrix}0\\1\end{pmatrix}}}$
${\displaystyle a[i][j][k]\leftarrow a[i][j][k-(t+1)(t+2)/2]}$

La routine π

Permutation des 25 mots avec un motif fixé: ${\displaystyle a[3i+2j][i]=a[i][j]}$

La routine χ

Combiner bit à bit des lignes selon la formule ${\displaystyle a=a\oplus (\lnot b\&c)}$:

${\displaystyle a[i][j][k]\leftarrow a[i][j][k]\oplus \lnot (a[i][j+1][k])\&(a[i][j+2][k])}$

Cette opération est la seule dite non linéaire.

La routine ι

Calculer le ou exclusif d’une constante avec un mot de l’état, qui dépend du numéro de l’itération ( n ):

pour chaque 0 ≤ m ≤ ℓ :${\displaystyle a[0][0][2^{m}-1]}$ est Xoré avec le bit numéroté m+7n d’une séquence LFSR de degré 8.

Cette dernière étape a pour objectif de casser les dernières symétries laissées par les précédentes.

La construction de l’éponge pour les fonctions de hachages. Les p_i sont l’entrée, les z_i sont l’empreinte en sortie. La « capacité » c, inutilisée, devrait être le double de la résistance voulue aux collisions ou aux attaques de préimage.

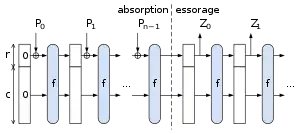
SHA-3 utilise la construction de l’éponge, dans laquelle l’entrée est, métaphoriquement dans une première phrase absorbée par l’état, à une certaine vitesse, et dans une deuxième essorée, à la même vitesse.

Pour absorber r bits des données, la donnée est XORée dans les premiers bits de l’état, puis la permutation par blocs est appliquée si une sortie additionnelle est désirée.

La capacité de la fonction de hachage, les c=25w-r bits d’états qui ne sont jamais directement touchés par l’entrée ou la sortie, est un paramètre important. Elle peut être ajustée en fonction de la sécurité attendue de la construction, mais la norme SHA-3 la fixe raisonnablement à c=2n, avec n la taille de l’empreinte voulue.

Ainsi r, la quantité de bits du message traitée à chaque permutation, dépend de la taille d’empreinte désirée. Les différents choix de taux r sont 1152, 1088, 832, ou 576 (144, 136, 104 ou 72 octets) pour des tailles d’empreinte de 224, 256, 384 et 512 bits, respectivement, pour w fixé à 64.

Pour aligner le message sur une taille multiple de la taille d’un bloc de r bits, il est comblé (par remplissage, ou padding en anglais) avec le motif binaire 10...01 : un premier bit à 1, suivi éventuellement du nombre approprié de bits à 0 (au maximum r-1 bits), mais toujours suivi d’un autre bit à 1. Ce dernier bit est une précondition nécessaire à la preuve de sécurité de la construction de l’éponge (le dernier bloc de message doit être non nul).

L’algorithme se déroule ainsi : l’état est initialisé à 0, l’entrée est comblée, découpée en blocs de r bits. L’entrée est absorbée par l’état, c’est-à-dire que pour chaque bloc elle est XORée avec l’état puis la permutation est appliquée sur le résultat.

Une fois toutes les permutations effectuées, l’empreinte résultat est constituée des n premiers bits de l’état. r est toujours plus grand que n, il n’y a par conséquent jamais besoin d’appliquer plusieurs permutations lors de la phase d’essorage. Dans d’autres applications comme Optimal Asymmetric Encryption Padding (OAEP) une sortie de taille variable est utile. Dans ce cas, n est un paramètre de sécurité plus qu’une simple taille de sortie.

Des variantes de la fonction de permutation permettant de générer des hachages plus petits sont également disponibles pour des tailles de hachage allant jusqu’à la moitié de la taille de leur état interne, si le taux r est suffisamment faible. Elles n’étaient pas nécessaire pour la candidature à la compétition SHA. Par exemple, il est possible de calculer une empreinte de 256 bits en utilisant 25 mots de 32 bits si r=800−2×256=288, soit 32 octets par itération.

SHA-3, instanciation la construction de l’éponge, pourrait s’écrire en pseudo-code :

fonction SHA-3(flux) :

paramètres de la construction :

f : une transformation de b bits → b bits, décrite dans la précédente section

r : le nombre de bits par bloc de sortie

pad : une fonction de comblement du flux d’entrée en blocs entiers de r bits

n_s : le nombre de blocs de sortie

variables internes :

état : un tableau de b bits, initialisés à 0, divisé en état[1..r] et état[r+1..b]

blocs : un tableau de blocs de r bits chacun

z : une chaîne à retourner, de longueur n_s×r, initialisée vide

algorithme :

(* phase d’absorption *)

blocs ← découpe pad(flux) en blocs de taille r bits

pour chaque p dans blocs :

état ← f(état[1..r] ⊕ p)

(* phase d’essorage *)

répéter n_s fois :

z ← concatène(z, état[1..r])

état ← f(état)

retourne z