Fonction de hachage cryptographique

Une fonction de hachage cryptographique est une fonction de hachage qui, à une donnée de taille arbitraire, associe une image de taille fixe, et dont une propriété essentielle est qu'elle est pratiquement impossible à inverser, c'est-à-dire que si l'image d'une donnée par la fonction se calcule très efficacement, le calcul inverse d'une donnée d'entrée ayant pour image une certaine valeur se révèle impossible sur le plan pratique. Pour cette raison, on dit d'une telle fonction qu'elle est à sens unique.

Une fonction de hachage cryptographique (spécifiquement, SHA-1) en action. Notez que même de petits changements dans la donnée d'entrée (ici dans le mot over) changent radicalement le résultat de sortie par un phénomène appelé effet avalanche.

En raison de leur ubiquité, ces fonctions à sens unique ont été appelées les chevaux de trait de la cryptographie moderne[1]. La donnée d'entrée de ces fonctions est souvent appelée message ; la valeur de sortie est souvent appelée valeur de hachage, empreinte numérique, empreinte, ou encore haché (en anglais, message digest ou digest, hash).

Une fonction de hachage cryptographique idéale possède les six propriétés suivantes[2] :

la fonction est déterministe, c'est-à-dire qu'un même message aura toujours la même valeur de hachage ;
la valeur de hachage d'un message se calcule « facilement » ;
il est impossible, pour une valeur de hachage donnée, de construire un message ayant cette valeur (résistance à la préimage) ;
il est impossible de trouver un second message ayant la même valeur de hachage qu'un message donné (résistance à la seconde préimage) ;
il est impossible de trouver deux messages différents ayant la même valeur de hachage (résistance aux collisions) ;
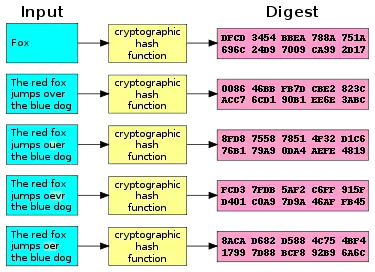
modifier un tant soit peu un message modifie considérablement la valeur de hachage[3].

Les fonctions de hachage cryptographiques sont une primitive de cryptographie symétrique, mais forment une brique de base largement utilisées dans la conception de schémas cryptographiques (aussi bien symétriques qu'asymétriques), notamment dans les signatures numériques, les codes d'authentification de message et les autres formes d'authentification.

Les fonctions Secure Hash Algorithm (SHA) du NIST sont des exemples de fonctions de hachage cryptographiques.

Propriétés

La plupart des fonctions de hachage cryptographiques sont conçues pour prendre une suite de bits de longueur quelconque en entrée (éventuellement la longueur est bornée, mais la borne est très élevée) et produire une valeur de hachage de longueur fixe en sortie.

Dans leur définition formelle, les fonctions de hachages cryptographiques possèdent dans le modèle standard différents niveaux de sécurités qui peuvent être requis[4], définis par les propriétés suivantes :

résistance à la préimage (en anglais, preimage resistance) pour toute valeur de hachage h, il devrait être difficile de trouver un message m tel que hachage(m) = h. Cette notion est liée à la notion de fonction à sens unique. Les fonctions qui n'ont pas cette propriété sont vulnérables aux attaques de préimage (en anglais, preimage attacks) ;
résistance à la seconde préimage (en anglais, second preimage resistance) pour tout message m₁, il devrait être difficile de trouver un message différent m₂ tel que hachage(m₁) = hachage(m₂). Les fonctions qui n'ont pas cette propriété sont vulnérables aux attaques de seconde préimage (en anglais, second-preimage attacks) ;
résistance aux collisions il doit être difficile de trouver deux messages différents m₁ et m₂ tels que hachage(m₁) = hachage(m₂). Une telle paire de messages est appelée une collision de hachage cryptographique. Pour obtenir cette propriété, il faut une valeur de hachage au moins deux fois plus longue que celle requise pour obtenir la résistance à la préimage. Si la clé n'est pas assez longue, une collision peut être trouvée par une attaque des anniversaires.

On peut noter qu'un algorithme permettant de trouver une préimage peut aussi être utilisé pour fournir une collision ; par contraposée, l'absence d'attaque efficace en collision implique l'absence d'attaque efficace en préimage. En pratique, les fonctions de hachages cryptographiques utilisées sont conçues pour être résistantes aux collisions, cette propriété impliquant les deux autres. Et même si en cryptographie théorique il est parfois nécessaire d’utiliser des fonctions de hachages sur des hypothèses plus faibles pour des raisons d'efficacité calculatoire théoriques, on leur préférera en pratique les fonctions standardisées possédant les propriétés de sécurité les plus fortes.

Informellement, ces propriétés signifient qu'un adversaire malveillant ne peut pas remplacer ou modifier les données d'entrée sans changer son empreinte numérique. Ainsi, si deux chaînes ont la même empreinte numérique, on peut être très confiant dans le fait qu'elles sont identiques.

Une fonction de hachage cryptographiquement sûre peut tout de même avoir des propriétés indésirables. Actuellement, des fonctions populaires de hachage cryptographique (MD5, SHA-1 et la plupart des SHA-2) sont vulnérables à des attaques qui allongent la longueur du message : en effet, si hachage(m₁) et la longueur de m₁ sont connus, en choisissant un m₂ approprié, un attaquant peut calculer hachage(m₁ || m₂) où || désigne la concaténation[5]. Cette particularité peut être utilisée pour briser des algorithmes d'authentification fondés sur des fonctions de hachage. Les HMAC (en anglais Keyed-Hash Message Authentication Code) permet de corriger cette faiblesse.

On pourrait augmenter la sécurité des fonctions de hachage cryptographiques en exigeant des propriétés additionnelles pour ces fonctions. Par exemple,

il est impossible de trouver deux messages ayant des empreintes numériques semblables ;
il est impossible de déduire quelque information que ce soit d'un message à partir de son empreinte numérique.

Les algorithmes de somme de contrôle (checksum), comme CRC32 et d'autres contrôles de redondance cyclique, sont conçus pour répondre à des exigences beaucoup plus faibles et sont généralement inadéquats comme fonctions de hachage cryptographique. Par exemple, un CRC a été utilisé pour vérifier l'intégrité des messages dans la norme de cryptage WEP, mais une attaque qui exploitait la linéarité de la somme de contrôle a été rapidement découverte[6].

Modèle de l'oracle aléatoire

Dans le cadre de la sécurité prouvable, le modèle de l'oracle aléatoire est un modèle de sécurité idéalisé où les fonctions de hachage cryptographiques sont considérées comme des fonctions aléatoires. Cette méthodologie permet de prouver des résultats qui ne sont pas possibles autrement. Par exemple la transformation de Fiat-Shamir repose essentiellement sur le fait que la fonction de hachage est utilisée comme une fonction aléatoire.

Cependant cette méthodologie est parfois critiquée car considérée comme non-réaliste[7], et on lui préférera le modèle standard et les définitions ci-dessus dans les cas où ils sont suffisants. Ainsi le premier chiffrement fondé sur l'identité (IBE) par Boneh et Franklin[8] est prouvé sûr dans le modèle de l'oracle aléatoire, avant la découverte de l'IBE par Boneh et Boyen[9] prouvé dans le modèle standard, n'utilisant que des fonctions de hachage résistantes aux collisions.

Degré de difficulté

Dans la pratique de la cryptographie, difficile signifie généralement au-delà de la portée de tout adversaire, et cela aussi longtemps que la sécurité du système est jugée importante. La signification du terme est dépendante de la valeur de l'information à protéger, puisque l'effort qu'un agent malveillant peut mettre à la tâche est généralement proportionnel à son espérance de gain. L'évaluation de la puissance de traitement d'un adversaire doit aussi tenir compte de la période de temps durant laquelle l'information doit être protégée. En effet, comme les connaissances cryptographiques et la puissance de traitement des ordinateurs augmentent rapidement, il faut tenir compte de ce fait pour estimer les capacités d'un adversaire dans 10 ou 20 ans. Toutefois, étant donné que l'effort nécessaire pour briser un message augmente très rapidement avec la longueur de la valeur de hachage, même une augmentation par un facteur de mille de la puissance de traitement peut être neutralisée par l'addition d'une dizaine de bits à la valeur de hachage.

Dans certaines analyses théoriques, difficile a le sens mathématique spécifique suivant : non résoluble dans un temps polynomial asymptotique. Cette définition de difficile est importante dans l'étude des fonctions de hachage cryptographiques pouvant être prouvées sécurisées, mais n'est généralement pas un gage de sécurité dans la pratique. Par exemple, un algorithme de temps exponentiel peut parfois être résoluble assez rapidement pour permettre une attaque. À l'inverse, un algorithme de temps polynomial (par exemple, celui qui nécessite n²⁰ étapes pour une clé de n chiffres) peut être trop lent pour une implémentation pratique.

Illustration

Voici un exemple d'utilisation d'un hachage cryptographique :

Alice propose un problème difficile de mathématiques à Bob, prétend qu'elle l'a résolu et défie Bob de le résoudre.
Bob veut bien essayer, mais il veut s'assurer qu'Alice ne bluffe pas.
Pour prouver sa bonne foi, Alice calcule la valeur de hachage de sa solution et la donne à Bob (tout en gardant sa solution secrète).
Si Bob résout le problème, il peut ensuite en calculer la valeur de hachage (en utilisant le même algorithme qu'Alice) et la comparer avec celle donnée par Alice à l'étape précédente. Si la solution est unique, les valeurs de hachage doivent être les mêmes. Alice a bien trouvé la solution avant Bob.

Le scénario précédent est un exemple d'une mise en gage simple. Dans la pratique, Alice et Bob seraient souvent des programmes informatiques et le secret serait quelque chose de moins facilement usurpée qu'une solution de puzzle.

Applications

Vérification de l'intégrité des fichiers ou des messages

Une application importante du hachage cryptographique est la vérification de l'intégrité d'un fichier (ou d'un message). Par exemple, la modification d'un fichier lors d'une transmission (ou toute autre activité) peut être prouvée en comparant la valeur de hachage du fichier avant et après la transmission.

En pratique, la plupart des algorithmes de signature numérique d'un fichier ne vérifient pas que le fichier n'a pas été changé, mais bien que la valeur de hachage du fichier n'a pas changé. Toutefois, à cause des caractéristiques des fonctions de hachage cryptographiques, la vérification de la valeur de hachage est considérée comme la preuve que le fichier lui-même est authentique.

Des valeurs de hachage obtenues par les algorithmes MD5, SHA-1 ou SHA-2 sont parfois affichées avec les fichiers correspondants sur des sites Web ou des forums informatiques pour permettre la vérification de l'intégrité des fichiers[10]. Cette pratique établit une chaîne de confiance pourvu que les valeurs de hachage soient affichées sur un site sécurisé par HTTPS.

La sécurité de la fonction de hachage utilisée, en particulier la résistance à une attaque par préimage est importante. Le ver informatique FLAME en 2012 a par exemple profité du fait que les certificats de confiance utilisés par Microsoft signaient une empreinte MD5[11] pour pouvoir s’installer discrètement en se faisant passer pour un composant système.

Vérification de mot de passe

Une autre application du hachage cryptographique est la vérification de mot de passe (inventée par Roger Needham). Le stockage de tous les mots de passe utilisateur en clair peut entraîner une violation de sécurité massive si le fichier de mots de passe est compromis. Une façon de réduire ce danger est de stocker seulement la valeur de hachage de chaque mot de passe. Pour authentifier un usager, le mot de passe fourni par l'utilisateur est haché et comparé avec la valeur de hachage stockée. Avec cette approche, les mots de passe perdus ne peuvent pas être récupérés s'ils sont oubliés ; ils doivent être remplacés par de nouveaux mots de passe.

Le mot de passe est souvent concaténé avec un sel cryptographique non secret avant que la fonction de hachage soit appliquée. Si le salage est aléatoire (sel différent pour chaque utilisateur) — ce qui est maintenant la norme —, le sel est stocké avec la valeur de hachage du mot de passe. Il est alors impossible de construire des tables de valeurs de hachage précalculées pour les mots de passe communs. Les fonctions de dérivation de clés, comme PBKDF2, Bcrypt ou Scrypt, typiquement utilisent des appels répétés d'une fonction de hachage cryptographique pour augmenter le temps nécessaire afin d'effectuer des attaques par force brute sur des valeurs de hachage de mots de passe stockés.

En 2013, une compétition de hachage de mots de passe, intitulée Password Hashing Competition a été annoncée pour choisir un nouvel algorithme standard de hachage de mot de passe[12]. Le 20 juillet 2015, Argon2 a été choisi comme le vainqueur de la compétition. Des mentions de reconnaissance ont aussi été attribuées aux hachages suivants : Catena, Lyra2 (en), Scrypt et Makwa[13].

Preuve de travail

Une preuve de travail est un protocole visant à dissuader les attaques par déni de service ou d'autres nuisances comme le spam, en exigeant du demandeur de service d’exécuter une tâche à coût non négligeable. Ce travail est habituellement un calcul complexe effectué par un ordinateur. Une caractéristique clé de ces travaux est leur asymétrie : le travail doit être modérément difficile à exécuter (mais possible) pour le demandeur, mais facilement vérifiable par le fournisseur de service. Une tâche typique exigée — par exemple, dans le minage de Bitcoins et Hashcash — est l'inversion partielle d'une fonction de hachage. Le demandeur doit trouver un message dont la valeur de hachage commence par un certain nombre de bits à zéro. Le coût moyen du travail que le requérant doit effectuer afin de trouver un message valide varie exponentiellement avec le nombre de zéros requis au début de la valeur de hachage, alors que le destinataire vérifie la validité de la réponse proposée en exécutant une seule fonction de hachage. Ainsi, avec Hashcash, un expéditeur doit générer un message dont la valeur de hachage commence par 20 zéros, par conséquent, il devra en moyenne essayer 2²⁰ messages pour trouver un message valide.

Identification de fichiers ou de données

Une valeur de hachage peut aussi servir comme un moyen d'identifier de manière fiable un fichier ; plusieurs systèmes de gestion de code source, y compris Git, Mercurial et Monotone, utilisent le sha1sum de divers types de contenu (le contenu de fichiers, les arborescences de répertoires, etc.) pour les identifier de manière unique. Les valeurs de hachage sont utilisées pour identifier les fichiers sur les réseaux de partage de fichiers pair-à-pair. Par exemple, dans un lien ed2k, la valeur de hachage d'une variante de MD4 est combinée avec la taille du fichier, fournissant des informations suffisantes pour localiser les sources du fichier, le télécharger et en vérifier le contenu.

L'une des principales applications d'une fonction de hachage est de permettre la consultation rapide d'un élément dans une table de hachage. Étant des fonctions de hachage d'un genre particulier, les fonctions de hachage cryptographiques se prêtent aussi à cette utilisation. Cependant, en comparaison avec les fonctions de hachage standards, les fonctions de hachage cryptographiques sont beaucoup plus coûteuses en calcul. Pour cette raison, elles sont utilisées seulement dans des contextes où il est nécessaire de se protéger contre les risques de falsification (la création de données avec la même valeur de hachage que les données attendues) par des participants potentiellement malveillants.

Génération d'éléments pseudo-aléatoires et dérivation de clés

Les fonctions de hachage cryptographiques peuvent également être utilisées dans la génération de nombres et de suites de bits pseudo-aléatoires, ou pour dériver de nouvelles clés ou de nouveaux mots de passe à partir d'une clé ou d'un mot de passe sécurisé.

Notes et références

(en) Bruce Schneier, « Cryptanalysis of MD5 and SHA: Time for a New Standard », sur Computerworld (consulté le 15 octobre 2014).
(en) Alfred J. Menezes, Paul C. van Oorschot et Scott A. Vanstone, Handbook of Applied Cryptography, CRC Press, 1996 (ISBN 0-8493-8523-7, lire en ligne).
(en) Saif Al-Kuwari, James H. Davenport et Russell J. Bradford, Cryptographic Hash Functions: Recent Design Trends and Security Notions, 2011 (lire en ligne)
Rogaway et Shrimpton 2004.
(en) « Flickr's API Signature Forgery Vulnerability », Thai Duong and Juliano Rizzo
(en) Nikita Borisov, Ian Goldberg et David Wagner, « (In)Security of the WEP algorithm » (consulté le 20 août 2016)
Müller-Quade et Unruh 2007, section 5.1. Trusted Devices Implementing a Random Oracle.
Boneh et Franklin 2001.
Boneh et Boyen 2004.
(en) Chad Perrin, « Use MD5 hashes to verify software downloads », TechRepublic, 5 décembre 2007 (consulté le 2 mars 2013)
Fillinger et Stevens 2015.
(en) « Password Hashing Competition » (consulté le 3 mars 2013)
"Password Hashing Competition"

Annexes

Bibliographie

[Boneh et Boyen 2004] (en) Dan Boneh et Xavier Boyen, « Efficient Selective-ID Secure Identity-Based Encryption Without Random Oracles », Eurocrypt,‎ 2004 (DOI 10.1007/978-3-540-24676-3_14)
[Boneh et Franklin 2001] (en) Dan Boneh et Matt Franklin, « Identity-Based Encryption from the Weil Pairing », Crypto,‎ 2001 (DOI 10.1007/3-540-44647-8_13)
[Fillinger et Stevens 2015] (en) Max Fillinger et Marc Stevens, « Reverse-Engineering of the Cryptanalytic Attack Used in the Flame Super-Malware », Asiacrypt,‎ 2015 (lire en ligne)
[Müller-Quade et Unruh 2007] (en) Jörn Müller-Quade et Dominique Unruh, « Long-Term Security and Universal Composability », Theory of Cryptography Conference (TCC),‎ 2007
[Rogaway et Shrimpton 2003] (en) Phillip Rogaway et Thomas Shrimpton, « Cryptographic Hash-Function Basics: Definitions, Implications, and Separations for Preimage Resistance, Second-Preimage Resistance, and Collision Resistance », FSE,‎ 2003 (lire en ligne)

Liens externes

(en) Christof Paar et Jan Pelzl, Understanding Cryptography, A Textbook for Students and Practitioners, Springer, 2009 (lire en ligne), « 11: Hash Functions » (companion web site contains online cryptography course that covers hash functions)
(en) « The ECRYPT Hash Function Website »

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.