Alice et Bob

• Alice et Bob (parfois Bernard en français). En général, Alice veut envoyer un message à Bob.
• Carol (ou Carole en français), est une troisième participante aux échanges. Puis, on a souvent Dave ou David[5], un quatrième participant. Pour aller au-delà, il faudrait utiliser un prénom en « E », mais un risque de confusion existe car cette lettre est celle de l'attaquant le plus courant (voir plus bas).

• Eve, une écouteuse externe (de l'anglais eavesdropper), est une attaquante passive. Elle peut écouter les échanges d'Alice et de Bob, mais elle ne peut pas les modifier. Ce personnage a été introduit dès 1988 par Charles Bennett, Gilles Brassard et Jean-Marc Robert[6].
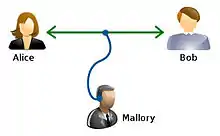
• Mallory, (ou Mallet, pour malicieux), est un attaquant actif. Au contraire d'Eve, Mallory peut modifier les messages, substituer les siens, remettre en jeu d'anciens messages, etc. Rendre un système sûr vis-à-vis de Mallory s'avère un problème plus difficile que pour Eve.
• Oscar, un opposant, est habituellement défini comme équivalent à Mallory.
• Trudy, une intruse, est plus dangereuse qu'Eve mais moins que Mallory car elle ne peut modifier des messages qu'en transit. Bob et Alice devraient idéalement être aptes à détecter de telles modifications, puis soit les ignorer, soit récupérer le message original. Sinon, Trudy peut causer beaucoup de dommages. Il faut noter que si on bloque Eve, Trudy sera bloquée également parce qu'elle ne pourra pas accéder aux messages.

• Isaac, un fournisseur d'accès à Internet (« i » de l'anglais Internet Service Provider, ISP).
• David, le développeur d'un logiciel.
• Susie, opératrice d'un serveur (de transit entre Alice et Bob, par exemple).
• Ivan, un émetteur (« i » de l'anglais issuer), pour la cryptographie financière, par exemple.
• Justin, du système de justice, plus spécifiquement, un avocat.
• Matilda, une marchande, pour la cryptographie financière ou le commerce électronique, par exemple.
• Nestor, un tiers de confiance neutre, est une version francophone de Trent.
• Plod, est un officier de police, de douanes ou de service de renseignements.
• Trent, est un arbitre de confiance (« tr » de l'anglais trusted arbitrator), est en quelque sorte un tiers parti neutre dont le rôle exact varie avec le protocole dont il est question.
• Vanna, voir Peggy.
• Victor, voir Peggy.
• Walter, un gardien de prison (« w » de l'anglais warden), peut surveiller Alice et Bob d'une façon qui dépend du protocole en question.

• Peggy (ou Pat), un prouveur et Victor (ou Venna) un vérifieur, doivent interagir d'une façon donnée afin de prouver que la transaction voulue a bien eu lieu. On les retrouve souvent dans les preuves à divulgation nulle de connaissance (zero-knowledge). La paire de noms Pat et Vanna viennent des hôtes de l'émission de télévision américaine Wheel of Fortune.

Bien que les systèmes de preuve interactive ne soient pas tout à fait des protocoles cryptographiques, ils sont suffisamment reliés pour qu'on mentionne la liste des personnages de sa terminologie.

• Arthur et Merlin : dans les preuves interactives, le prouveur a une capacité calculatoire illimitée et est donc associé à Merlin, le puissant magicien. Il émet un énoncé comme véritable et Arthur, le sage roi, lui pose des questions pour vérifier cet énoncé. Ces deux personnages sont aussi éponymes de deux classes de complexité, soit MA et AM.

• [Bennett, Brassard et Robert 1988] (en) Charles H. Bennett, Gilles Brassard et Jean-Marc Robert, « Privacy Amplification by Public Discussion », SIAM Journal on Computing, vol. 17, n^o 2,‎ avril 1988, p. 210-229 (ISSN 0097-5397 et 1095-7111, DOI 10.1137/0217014, lire en ligne, consulté le 11 mai 2021) ;
• [Rivest, Shamir et Adleman 1978] (en) R. L. Rivest, A. Shamir et L. Adleman, « A method for obtaining digital signatures and public-key cryptosystems », Communications of the ACM, vol. 21, n^o 2,‎ février 1978, p. 120-126 (ISSN 0001-0782 et 1557-7317, DOI 10.1145/359340.359342, lire en ligne, consulté le 11 mai 2021) ;
• [Schneier 2015] Bruce Schneier, Applied cryptography : protocols, algorithms, and source code in C, 2015 (ISBN 978-1-119-18347-1, 1-119-18347-2 et 978-1-119-43902-8, OCLC 914287736, lire en ligne) ;
• [Xue, Wang et Wang 2017] (en) Peng Xue, Kunkun Wang et Xiaoping Wang, « Efficient multiuser quantum cryptography network based on entanglement », Scientific Reports, vol. 7, n^o 1,‎ mai 2017 (ISSN 2045-2322, PMID 28374854, PMCID PMC5379677, DOI 10.1038/srep45928, lire en ligne, consulté le 11 mai 2021).

• [Brown 2005] (en) Bob Brown, « Security's inseparable couple : Alice & Bob », sur Network World, 7 février 2005 (consulté le 11 mai 2021) ;
• [DuPont et Cattapan 2017] (en) Quinn DuPont et Alana Cattapan, « Alice & Bob : A History of The World’s Most Famous Cryptographic Couple », 2017 (consulté le 11 mai 2021).