Cryptographie asymétrique
La cryptographie asymétrique, ou cryptographie à clé publique est un domaine relativement récent de la cryptographie. Elle permet d'assurer la confidentialité d'une communication, ou d'authentifier les participants, sans que cela repose sur une donnée secrète partagée entre ceux-ci, contrairement à la cryptographie symétrique qui nécessite ce secret partagé préalable[1].

La cryptographie asymétrique peut être illustrée avec l'exemple du chiffrement à clé publique et privée, dont le but, comme tout chiffrement, est de garantir la confidentialité d'une donnée lors d'une transmission de celle-ci. Le terme asymétrique s'explique par le fait qu'il utilise deux clés différentes, l'une, la clé publique, pour chiffrer, l'autre, la clé privée, pour déchiffrer. L'utilisateur qui souhaite recevoir des messages engendre un tel couple de clés. Il ne transmet à personne la clé privée alors que la clé publique est transmissible sans restriction[2]. Quiconque souhaite lui envoyer un message confidentiel utilise la clé publique pour chiffrer celui-ci. Le message chiffré obtenu ne peut être déchiffré que connaissant la clé privée. Il peut donc être communiqué publiquement : la confidentialité du message original est garantie. Le destinataire, qui n'a communiqué à personne sa clé privée, est le seul à pouvoir, à l'aide de celle-ci, déchiffrer le message transmis pour reconstituer le message original[1].
Un problème crucial pour l'émetteur est de s'assurer que la clé publique qu'il utilise est bien celle du destinataire souhaité[1].
Ce système a deux utilisations majeures :
- la confidentialité des messages reçus : c'est celle qu'on vient de décrire, l'expéditeur utilise la clé publique du destinataire pour chiffrer son message. Le destinataire utilise sa clé privée pour déchiffrer le message de l'expéditeur, garantissant la confidentialité du contenu ;
- l'authentification de l'expéditeur d'un message (pas nécessairement confidentiel) : l'expéditeur utilise sa clé privée pour chiffrer un message que n'importe qui peut déchiffrer avec la clé publique de l'expéditeur, ce qui garantit que le message a été chiffré par l'expéditeur, seul à posséder la clé privée ; c'est le mécanisme utilisé par la signature numérique pour authentifier l'auteur d'un message[3].
Historique
Concept
Le concept de cryptographie à clé publique — autre nom de la cryptographie asymétrique — est généralement attribué à Whitfield Diffie et à Martin Hellman qui l'ont présenté au public à la National Computer Conference en 1976[4], puis publié quelques mois plus tard dans New Directions in Cryptography[5]. Le concept aurait cependant été découvert indépendamment par d'autres chercheurs à la même époque.
Ralph Merkle aurait fait la même découverte à la même époque[6], même si ses articles[7] ne furent publiés qu'en 1978.
Mise en œuvre
Dans leur article de 1976, W. Diffie et M. Hellman n'avaient pas pu donner l'exemple d'un système à clé publique, n'en ayant pas trouvé. Il fallut attendre 1978 pour avoir un exemple[8] donné par Ronald Rivest, Adi Shamir et Leonard Adleman, le RSA, abréviation tirée des trois noms de ses auteurs. Les trois hommes fondèrent par la suite la société RSA Security. Le système Merkle-Hellman[9] est généralement considéré comme la première réalisation pratique d'un système de chiffrement à clé publique[10], il a cependant été prouvé non sûr par Shamir en 1982[11].
Recherches secrètes du GCHQ
Parallèlement aux recherches publiques, les services du chiffre britannique (GCHQ, Government Communications Headquarters) auraient mené des recherches secrètes aboutissant à des concepts et outils de chiffrement asymétrique dès la première moitié des années 1970[12] :
- James Ellis, du GCHQ aurait proposé le concept avant Hellman et Diffie;
- Clifford Cocks aurait décrit dès 1973 ce qu'on appelle l'algorithme RSA ;
- Malcolm J. Williamson aurait inventé un protocole d'échange de clé très proche de celui de Diffie et de Hellman dès 1974.
Ces découvertes n'auraient été rendues publiques par le GCHQ qu'en 1997[12].
Découverte publique
En 1976, un cryptosystème à clé asymétrique a été publié par Whitfield Diffie et Martin Hellman qui, influencés par les travaux de Ralph Merkle sur la distribution de clé publique, ont divulgué une méthode d'accord de clé publique. Cette méthode d'échange de clés, qui utilise l'exponentiation dans un corps fini, est devenue connue sous le nom d'échange de clés Diffie-Hellman[13]. Il s'agissait de la première méthode pratique publiée pour établir une clé secrète partagée sur un canal de communication authentifié (mais non confidentiel) sans utiliser de secret partagé préalable. La « technique d'accord de clé publique » de Merkle, devenue connue sous le nom de Merkle's Puzzles, a été inventée en 1974 et publiée seulement en 1978. Cela fait du chiffrement asymétrique un domaine plutôt nouveau de la cryptographie, bien que la cryptographie en elle-même remonte à plus de 2 000 ans[14].
En 1977, une généralisation du schéma de Cocks a été inventée indépendamment par Ronald Rivest, Adi Shamir et Leonard Adleman, tous alors au MIT. Ces derniers auteurs ont publié leurs travaux en 1978 dans la colonne Scientific American de Martin Gardner, et l'algorithme est devenu connu sous le nom de RSA, leurs initiales. RSA utilise l'exponentiation modulo un produit de deux très grands nombres premiers, pour chiffrer et déchiffrer, effectuant à la fois le chiffrement à clé publique et les signatures numériques à clé publique. Sa sécurité est liée à l'extrême difficulté de factoriser de grands entiers, un problème pour lequel il n'y a pas de technique générale efficace connue (bien que la factorisation première puisse être obtenue par des attaques par force brute ; cela devient d'autant plus difficile que les facteurs premiers sont très grands). Une description de l'algorithme a été publiée dans la colonne Mathematical Games du numéro d'août 1977 de Scientific American[15].
Depuis les années 1970, un grand nombre et une grande variété de techniques de chiffrement, de signature numérique, d'accord de clé et d'autres techniques ont été développées, notamment le cryptosystème Rabin, le chiffrement ElGamal, le DSA et la cryptographie à courbe elliptique.
Fonctionnement
Principe général
La cryptographie asymétrique, ou cryptographie à clé publique est fondée sur l'existence de fonctions à sens unique et à trappe secrète.
Les fonctions à sens unique sont des fonctions mathématiques telles qu'une fois appliquées à un message, il est extrêmement difficile de retrouver le message original.
L'existence d'une trappe secrète permet cependant à la personne qui a conçu la fonction à sens unique de déchiffrer facilement le message grâce à un élément d'information qu'elle possède, appelé clé privée.
Supposons qu'Alice souhaite recevoir un message secret de Bob sur un canal susceptible d'être écouté par un attaquant passif Eve :
- Alice transmet à Bob une fonction à sens unique pour laquelle elle seule connait la trappe secrète ;
- Bob utilise la fonction transmise par Alice pour chiffrer son message secret ;
- Alice réceptionne le message chiffré puis le déchiffre grâce à la trappe secrète ;
- Si Eve réceptionne également le message alors qu'il circule sur le canal public, elle ne peut le déchiffrer, même si elle a également intercepté l'envoi de la fonction à sens unique, car elle n'a pas connaissance de la trappe secrète.
La terminologie classiquement retenue est :
- pour la fonction à sens unique : « clé publique » ;
- pour la trappe secrète : « clé privée ».
En pratique, sont utilisées des fonctions de chiffrement classiques, les termes « clé publique » et « clé privée » correspondant alors à des paramètres employés pour ces fonctions.
Fonctionnement pratique
Alice souhaite pouvoir recevoir des messages chiffrés de n'importe qui.
Diffusion des clés publiques
Elle génère alors une valeur à partir d'une fonction à sens unique et à trappe secrète à l'aide d'un algorithme de chiffrement asymétrique (liste ici), par exemple RSA[16].
Alice diffuse à tout le monde la fonction pour chiffrer les messages (notée clé publique) mais garde secrète la fonction de décodage (notée clé privée).

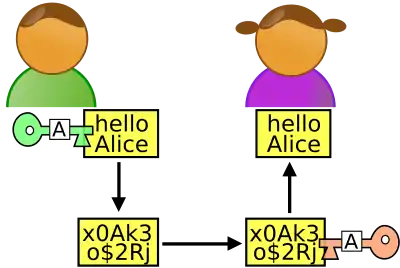
Chiffrement
L'un des rôles de la clé publique est de permettre le chiffrement ; c'est donc cette clé qu'utilisera Bob pour envoyer des messages chiffrés à Alice. L'autre clé — l'information secrète — sert à déchiffrer. Ainsi, Alice, et elle seule, peut prendre connaissance des messages de Bob. La connaissance d'une clé ne permet pas de déduire l'autre.
Authentification de l'origine
D'autre part, l'utilisation par Alice de sa clé privée sur le condensat d'un message, permettra à Bob de vérifier que le message provient bien d'Alice : il appliquera la clé publique d'Alice au condensat fourni (condensat chiffré avec la clé privée d'Alice) et retrouve donc le condensat original du message. Il lui suffira de comparer le condensat ainsi obtenu et le condensat réel du message pour savoir si Alice est bien l'expéditeur. C'est donc ainsi que Bob sera rassuré sur l'origine du message reçu : il appartient bien à Alice. C'est sur ce mécanisme notamment que fonctionne la signature numérique.
Analyse fonctionnelle
Le coffre-fort
Le chiffrement : Alice a choisi un coffre-fort. Elle l'envoie ouvert à Bob, et en garde la clé. Lorsque Bob veut écrire à Alice, il y dépose son message, ferme le coffre, il n'a pas besoin de la clé pour cela, et le renvoie à Alice. À sa réception, seule Alice peut ouvrir le coffre, puisqu'elle seule en possède la clé, à supposer le coffre inviolable, et que personne ne puisse refaire la clé.
L'authentification ou la signature : Alice place un message dans le coffre-fort qu'elle ferme avec sa clé privée avant de l'envoyer à Bob. Si Bob parvient à ouvrir le coffre à l'aide de la clé publique d'Alice (dont il dispose), c'est que c'est bien le coffre fermé par Alice puisque la clé de Bob ne permet d'ouvrir que les coffres fermés par Alice. Bob est donc certain que c'est bien Alice qui y a placé le message.
La boîte à deux serrures
Une autre analogie envisageable serait d'imaginer une boîte avec deux serrures différentes. Lorsque l'on ferme la boîte d'un côté, seule la clé correspondant à l'autre serrure permet l'ouverture de la boîte et vice-versa. Une des clés est privée et conservée secrète, l'autre est dite publique et un exemplaire peut-être obtenu par quiconque souhaite utiliser la boîte.
Pour chiffrer un message Bob prend la boîte, y place son message, et la ferme à l'aide de la clé publique. Seul le détenteur de la clé privée permettant d'accéder à l'autre serrure, Alice en l'occurrence, sera en mesure de rouvrir la boîte.
Pour signer un message, Alice le place dans la boîte et ferme celle-ci à l'aide de sa clé privée. Ainsi n'importe qui ayant récupéré la clé publique pourra ouvrir la boîte. Mais comme la boîte a été fermée par la clé privée, cette personne sera assurée que c'est bien Alice, seule détentrice de cette clé, qui aura placé le message dans la boîte et fermé ladite boîte.
Inconvénients et limites
Comme pour tous les systèmes liés à la sécurité, il est important d'identifier les faiblesses potentielles. Outre le mauvais choix d'un algorithme à clé asymétrique (il y en a peu qui sont largement considérés comme satisfaisants) ou une longueur de clé trop courte, le principal risque de sécurité est que la clé privée d'une paire soit connue. En contrepartie de leurs propriétés spécifiques, les chiffrements asymétriques sont globalement moins performants que leurs équivalents symétriques : les temps de traitement sont plus longs et, pour un niveau de sécurité équivalent, les clés doivent être beaucoup plus longues.
Algorithmes
Tous les schémas à clé publique sont en théorie sensibles à une "attaque par force brute"[17]. Cependant, une telle attaque n'est pas pratique si la quantité de calcul nécessaire pour réussir - appelé le "facteur de travail" par Claude Shannon - est hors de portée de tous les attaquants potentiels. Dans de nombreux cas, le facteur de travail peut être augmenté en choisissant simplement une clé plus longue. Mais d'autres algorithmes peuvent intrinsèquement avoir des facteurs de travail beaucoup plus faibles, ce qui rend la résistance à une attaque par force brute (par exemple, à partir de touches plus longues) non pertinente. Certains algorithmes spéciaux et spécifiques ont été développés pour aider à attaquer certains algorithmes de cryptage à clé publique ; le RSA et système de cryptage ElGamal ont des attaques connues qui sont beaucoup plus rapides que l'approche de la force brute[18]. Cependant, aucun d'entre eux n'est suffisamment amélioré pour être réellement pratique.
Des faiblesses majeures ont été trouvées pour plusieurs algorithmes de clés asymétriques autrefois prometteurs. Le cryptosystème Merkle – Hellman a été jugé peu sûr après le développement d'une nouvelle attaque[19]. Comme pour toutes les fonctions cryptographiques, les implémentations à clé publique peuvent être vulnérables aux attaques par canal auxiliaire qui exploitent les fuites d'informations pour simplifier la recherche d'une clé secrète. Ceux-ci sont souvent indépendants de l'algorithme utilisé. Des recherches sont en cours pour à la fois découvrir et se protéger contre de nouvelles attaques.
Altération des clés publiques
Une autre vulnérabilité de sécurité potentielle dans l'utilisation de clés asymétriques est la possibilité d'une attaque "man-in-the-middle", dans laquelle la communication des clés publiques est interceptée par un tiers (le "man in the middle") puis modifiée pour fournir des clés publiques différentes à la place. Les messages et les réponses chiffrés doivent, dans tous les cas, être interceptés, déchiffrés et rechiffrés par l'attaquant à l'aide des clés publiques correctes pour les différents segments de communication afin d'éviter tout soupçon.
Une communication est dite non sécurisée lorsque les données sont transmises d'une manière qui permet l'interception (également appelée "reniflage"). Ces termes font référence à la lecture des données privées de l'expéditeur dans leur intégralité. Une communication est particulièrement dangereuse lorsque les interceptions ne peuvent être empêchées ou surveillées par l'expéditeur[20].
Une attaque de l'homme du milieu peut être difficile à mettre en œuvre en raison de la complexité des protocoles de sécurité modernes. Cependant, la tâche devient plus simple lorsqu'un expéditeur utilise des médias non sécurisés tels que des réseaux publics, Internet ou une communication sans fil. Dans ces cas, un attaquant peut compromettre l'infrastructure de communication plutôt que les données elles-mêmes. Un membre du personnel malveillant hypothétique d'un fournisseur d'accès Internet (FAI) pourrait trouver une attaque de l'homme du milieu relativement simple. La capture de la clé publique nécessiterait uniquement de rechercher la clé lorsqu'elle est envoyée via le matériel de communication du FAI ; dans les schémas de clés asymétriques correctement mis en œuvre, ce n'est pas un risque significatif.
Dans certaines attaques avancées de l'homme du milieu, un côté de la communication verra les données d'origine tandis que l'autre recevra une variante malveillante. Les attaques asymétriques de l'homme du milieu peuvent empêcher les utilisateurs de réaliser que leur connexion est compromise. Cela reste le cas même lorsque les données d'un utilisateur sont connues pour être compromises parce que les données semblent correctes pour l'autre utilisateur. Cela peut conduire à des désaccords déroutants entre les utilisateurs tels que "ce doit être de votre côté !" lorsque aucun des utilisateurs n'est en faute. Par conséquent, les attaques de l'homme du milieu ne peuvent être entièrement évitées que lorsque l'infrastructure de communication est physiquement contrôlée par l'une ou les deux parties ; par exemple via une route câblée à l'intérieur du propre bâtiment de l'expéditeur. En résumé, les clés publiques sont plus faciles à modifier lorsque le matériel de communication utilisé par un expéditeur est contrôlé par un attaquant[21] - [22] - [23].
Infrastructure à clés publiques
Une approche pour prévenir de telles attaques implique l'utilisation d'une infrastructure à clé publique (PKI) ; un ensemble de rôles, de politiques et de procédures nécessaires pour créer, gérer, distribuer, utiliser, stocker et révoquer des certificats numériques et gérer le chiffrement à clé publique.
Cependant, cela a des faiblesses potentielles. Par exemple, l'autorité de certification émettant le certificat doit être reconnue par toutes les parties participantes pour avoir correctement vérifié l'identité du détenteur de la clé, pour s'être assurée de l'exactitude de la clé publique lorsqu'elle émet un certificat, pour être à l'abri du piratage informatique, et avoir pris des dispositions avec tous les participants pour vérifier tous leurs certificats avant que les communications protégées puissent commencer.
Malgré ses problèmes théoriques et potentiels, cette approche est largement utilisée. Les exemples incluent TLS et son prédécesseur SSL, qui sont couramment utilisés pour assurer la sécurité des transactions du navigateur Web (par exemple, pour envoyer en toute sécurité les détails de la carte de crédit à une boutique en ligne).
Outre la résistance à l'attaque d'une paire de clés particulière, la sécurité de la hiérarchie de certification doit être prise en compte lors du déploiement de systèmes à clé publique. Certaines autorités de certification - généralement un programme spécialement conçu à cet effet et exécuté sur un ordinateur serveur - garantissent les identités attribuées à des clés privées spécifiques en produisant un certificat numérique. Les certificats numériques à clé publique sont généralement valides pendant plusieurs années à la fois, de sorte que les clés privées associées doivent être conservées en toute sécurité pendant cette période. Lorsqu'une clé privée utilisée pour la création de certificats à un niveau supérieur dans la hiérarchie du serveur PKI est compromise ou accidentellement divulguée, une "attaque de l'homme au milieu" est possible, rendant tout certificat subordonné totalement non sécurisé.
Articulation avec le chiffrement symétrique
La cryptographie asymétrique répond à un besoin majeur de la cryptographie symétrique : le partage sécurisé d'une clé entre deux correspondants, afin de prévenir l'interception de cette clé par une personne tierce non autorisée, et donc la lecture des données chiffrées sans autorisation.
Les mécanismes de chiffrement symétrique étant moins coûteux en temps de calcul, ceux-ci sont préférés aux mécanismes de chiffrement asymétrique. Cependant toute utilisation de clé de chiffrement symétrique nécessite que les deux correspondants se partagent cette clé, c'est-à-dire la connaissent avant l'échange. Ceci peut être un problème si la communication de cette clé s'effectue par l'intermédiaire d'un medium non sécurisé, « en clair ». Afin de pallier cet inconvénient, on utilise un mécanisme de chiffrement asymétrique pour la seule phase d'échange de la clé symétrique, et l'on utilise cette dernière pour tout le reste de l'échange.
Applications
Mécanismes d'authentification
Un inconvénient majeur de l'utilisation des mécanismes de chiffrement asymétriques est le fait que la clé publique est distribuée à toutes les personnes : Bob, Carole et Alice souhaitant échanger des données de façon confidentielle. De ce fait, lorsque la personne possédant la clé privée, Alice, déchiffre les données chiffrées, elle n'a aucun moyen de vérifier avec certitude la provenance de ces données (Bob ou Carole) : on parle de problèmes d'authentification.
Afin de résoudre ce problème, on utilise des mécanismes d'authentification permettant de garantir la provenance des informations chiffrées. Ces mécanismes sont eux aussi fondés sur le chiffrement asymétrique dont le principe est le suivant : Bob souhaite envoyer des données chiffrées à Alice en lui garantissant qu'il en est l'expéditeur.
- Bob crée une paire de clés asymétriques : il définit une clé privée et diffuse librement sa clé publique (notamment à Alice)
- Alice crée une paire de clés asymétriques : elle définit une clé privée et diffuse librement sa clé publique (notamment à Bob)
- Bob effectue un condensat de son message « en clair » puis chiffre ce condensat avec sa clé privée
- Bob chiffre une seconde fois son message déjà chiffré avec la clé publique d'Alice
- Bob envoie alors le message chiffré à Alice
- Alice reçoit le message chiffré de Bob (mais qu'un tiers, par exemple Ève, pourrait intercepter)
- Alice est en mesure de déchiffrer le message avec sa clé privée. Elle obtient alors un message lisible sous forme de condensat. Eve quant à elle ne peut pas déchiffrer le message intercepté de Bob car elle ne connait pas la clé privée d'Alice. En revanche Alice n'est pas sûre que le message déchiffré (sous forme de condensat) est bien celui de Bob
- Pour le lire, Alice va alors déchiffrer le condensat (chiffré avec la clé privée de Bob) avec la clé publique de Bob. Par ce moyen, Alice peut avoir la certitude que Bob est l'expéditeur. Dans le cas contraire, le message est indéchiffrable et elle pourra présumer qu'une personne malveillante a tenté de lui envoyer un message en se faisant passer pour Bob
Cette méthode d'authentification utilise la spécificité des paires de clés asymétriques : si l'on chiffre un message en utilisant la clé publique, alors on peut déchiffrer le message en utilisant la clé privée ; l'inverse est aussi possible : si l'on chiffre en utilisant la clé privée alors on peut déchiffrer en utilisant la clé publique.
Certificats
La cryptographie asymétrique est également utilisée avec les certificats numériques, celui-ci contenant la clé publique de l'entité associée au certificat. La clé privée est quant à elle stockée au niveau de cette dernière entité. Une application des certificats est par exemple la mise en œuvre d'une infrastructure à clés publiques (PKI) pour gérer l'authentification et la signature numérique d'une entité, par exemple un serveur web (Apache avec le module SSL par exemple), ou simplement un client souhaitant signer et chiffrer des informations à l'aide de son certificat de la façon décrite dans les sections précédentes.
Sécurité
Un chiffrement symétrique au moyen d'une clé de 128 bits propose 2128 (~ 3,4 1038) façons de chiffrer un message. Un pirate qui essaierait de déchiffrer le message par la force brute devrait les essayer une par une.
Pour les systèmes à clé publique, il en va autrement. Tout d'abord les clés sont plus longues (par exemple 2048 bits minimum pour RSA) ; en effet, elles possèdent une structure mathématique très particulière (on ne peut pas choisir une suite de bits aléatoire comme clé secrète, par exemple dans le cas du RSA, seuls les nombres premiers sont utilisés). Certains algorithmes exploitant cette structure sont plus efficaces qu'une recherche exhaustive sur, par exemple, 1 024 bits. Ainsi, dans le cas de RSA, le crible général par corps de nombres (NFS en anglais) est une méthode plus efficace que la recherche exhaustive pour la factorisation.
Il faut noter le développement actuel de la cryptographie utilisant les courbes elliptiques, qui permettent (au prix d'une théorie et d'implémentations plus complexes) l'utilisation de clés nettement plus petites que celles des algorithmes classiques (une taille de 160 bits étant considérée comme très sûre actuellement), pour un niveau de sécurité équivalent.
Dans son édition du 6 septembre 2013, le journal The Guardian affirmait que la NSA était capable de déchiffrer la plupart des données chiffrées circulant sur Internet[24]. De nombreuses sources ont cependant indiqué que la NSA n'avait pas mathématiquement cassé les chiffrements mais s'appuierait sur des faiblesses d'implémentation des protocoles de sécurité[25] - [26].
Notes et références
- Katz et Lindell 2014, p. 375.
- GPG Handbook
- Katz et Lindell 2014, p. 439.
- Diffie et Hellman juin 1976.
- Diffie et Hellman novembre 1976.
- Menezes, Van Oorschot et Vanstone 1997, p. 47.
- Merkle 1978.
- Rivest, Shamir et Adleman 1978.
- Merkle et Hellman 1978.
- Menezes, Van Oorschot et Vanstone 1997, p. 300.
- Shamir 1983.
- Singh 1999.
- (en) W. Diffie et M. Hellman, « New directions in cryptography », IEEE Transactions on Information Theory, vol. 22, no 6, , p. 644–654 (ISSN 0018-9448, DOI 10.1109/TIT.1976.1055638, lire en ligne, consulté le )
- Sara Robinson, « Still Guarding Secrets after Years of Attacks, RSA Earns Accolades for its Founders », SIAM News, vol. 36, no 5, (lire en ligne)
- Rivest, Shamir et Adleman 1983.
- Christof Paar, Jan Pelzl et Bart Preneel, Understanding Cryptography: A Textbook for Students and Practitioners, Springer, (ISBN 978-3-642-04100-6, lire en ligne)
- Mavroeidis, Vasileios, and Kamer Vishi, "The Impact of Quantum Computing on Present Cryptography", International Journal of Advanced Computer Science and Applications, 31 March 2018
- Adi Shamir, « A polynomial time algorithm for breaking the basic Merkle-Hellman cryptosystem », 23rd Annual Symposium on Foundations of Computer Science (SFCS 1982), , p. 145–152 (DOI 10.1109/SFCS.1982.5, lire en ligne)
- Abi Tunggal, « What Is a Man-in-the-Middle Attack and How Can It Be Prevented - What is the difference between a man-in-the-middle attack and sniffing? », sur UpGuard, (consulté le )
- Abi Tunggal, « What Is a Man-in-the-Middle Attack and How Can It Be Prevented - Where do man-in-the-middle attacks happen? », sur UpGuard, (consulté le )
- martin, « China, GitHub and the man-in-the-middle » [archive du ], sur GreatFire, (consulté le )
- percy, « Authorities launch man-in-the-middle attack on Google », sur GreatFire, (consulté le )
- Ball, Borger et Greenwald 2013.
- Schneier 2013.
- Simonite 2013.
Annexes
Bibliographie
- [Barthélemy, Rolland et Véron 2005] Pierre Barthélemy, Robert Rolland et Pascal Véron (préf. Jacques Stern), Cryptographie : principes et mises en œuvre, Paris, Hermes Science Publications : Lavoisier, coll. « Collection Informatique », , 414 p., broché (ISBN 2-7462-1150-5, ISSN 1242-7691, OCLC 85891916).
- [Diffie et Hellman juin 1976] (en) Whitfield Diffie et Martin E. Hellman, « Multiuser cryptographic technics », Proceedings of AFIPS National Computer Conference, , p. 109-112 (DOI 10.1145/1499799.1499815).
- [Diffie et Hellman novembre 1976] (en) Whitfield Diffie et Martin E. Hellman, « New directions in cryptography », IEEE Trans. Inf. Theory, vol. 22, no 6, , p. 644-654.
- [Katz et Lindell 2014] (en) Jonathan Katz et Yehuda Lindell, Introduction to Modern Cryptography, 2nd Edition, Boca Raton, Chapman and Hall, , 583 p. (ISBN 978-1-4665-7026-9, lire en ligne), III. Public-Key (Asymmetric) Cryptography.
- [Menezes, Van Oorschot et Vanstone 1997] (en) A. J. Menezes, P. C. Van Oorschot et S. A. Vanstone, Handbook of Applied Cryptography, Boca Raton, CRC Press, coll. « CRC Press Series on Discrete Mathematics and Its Applications », , 780 p. (ISBN 978-0-8493-8523-0, OCLC 247238920).
- [Merkle 1978] (en) Ralph C. Merkle, « Secure communications over insecure channels », Communications of the ACM, vol. 21, , p. 294-299.
- [Merkle et Hellman 1978] (en) Ralph C. Merkle et Martin E. Hellman, « Hiding information and signatures in trapdoor functions », IEEE Trans. Inf. Theory, vol. 24, , p. 525-530.
- [Rivest, Shamir et Adleman 1978] (en) Ronald Rivest, Adi Shamir et Leonard Adleman, « A method for obtaining digital signatures and public-key cryptosystems », Communications of the ACM, vol. 21, , p. 120-126 (lire en ligne).
- [Rivest, Shamir et Adleman 1983] (en) Ronald L. Rivest, Adi Shamir et Leonard L. Adleman, « Cryptographic communications system and method », United States Patent, no 4405829, (lire en ligne).
- [Shamir 1983] (en) Adi Shamir, « A polynomial time algorithm for breaking the basic Merkle-Hellman crypto-system », Advances in cryptology, Proceedings of Crypto 82, , p. 279-288.
- [Singh 1999] Simon Singh (trad. de l'anglais par Catherine Coqueret), Histoire des codes secrets : De l'Égypte des pharaons à l'ordinateur quantique [« The code Book »], Paris, Jean-Claude Lattès, , 430 p. (ISBN 978-2-7096-2048-2, OCLC 43323003), chap. 6 (« Alice et Bernard s'affichent en public »).
Articles connexes
- Cryptographie hybride
- Infrastructures à clés Publiques (PKI)
- Authentification
- Authentification forte
- Alice et Bob
- Signature numérique
- Chiffrement
- Chiffrement fondé sur l'identité
- Chiffrement par attributs
- Liste d’algorithmes de cryptographie asymétrique
Logiciels de cryptographie asymétrique
- Pretty Good Privacy ou PGP, logiciel existant en versions payante et gratuite (aux fonctionnalités plus réduites).
- GNU Privacy Guard ou GPG ou GnuPG, version Libre (open-source) et gratuite de PGP.
- OpenSSL (Open Secure Socket Layer), version libre et gratuite permettant, notamment, de développer des fonctionnalités à base de chiffrement asymétrique.
- Acid Cryptofiler, logiciel développé par la Délégation Générale pour l'armement pour un usage gouvernemental.
Liens externes
- [Ball, Borger et Greenwald 2013] (en) James Ball, Julian Borger et Glenn Greenwald, « Revealed : how US and UK spy agencies defeat internet privacy and security », sur The Guardian, (consulté le ).
- [Schneier 2013] (en) Bruce Schneier, « The NSA Is Breaking Most Encryption on the Internet », sur Schneier on Security, (consulté le ).
- [Simonite 2013] (en) Tom Simonite, « NSA Leak Leaves Crypto-Math Intact but Highlights Known Workarounds », sur MIT Technology Review, (consulté le ).
- [GPG] (en) « The GNU Privacy Handbook » (consulté le )