Cryptosystème de ElGamal
Le cryptosystème d'ElGamal, ou chiffrement El Gamal (ou encore système d'El Gamal) est un protocole de cryptographie asymétrique inventé par Taher Elgamal en 1984[1] et construit à partir du problème du logarithme discret.
Ce protocole est utilisé par le logiciel libre GNU Privacy Guard[2] dont les versions récentes implémentent jusqu'à sa version sur les courbes elliptiques[3]. Contrairement au chiffrement RSA, il n’a jamais été sous la protection d’un brevet.
L’article fondateur par Taher Elgamal présente un protocole de chiffrement, mais aussi une signature numérique, qui malgré leurs similarités (ils sont tous deux construit sur le problème du logarithme discret) ne sont pas à confondre. Cet article traite uniquement du protocole de chiffrement.
Description de l’algorithme
L'algorithme est décrit pour un groupe cyclique fini au sein duquel le problème de décision de Diffie-Hellman (DDH) est difficile. Des informations plus précises sont données dans la section Résistance aux attaques CPA.
On peut remarquer que DDH est une hypothèse de travail plus forte que celle du logarithme discret, puisqu’elle tient si jamais le problème du logarithme discret est difficile. Il existe par ailleurs des groupes où le problème DDH est facile, mais où on n'a pas d'algorithme efficace pour résoudre le logarithme discret[4].
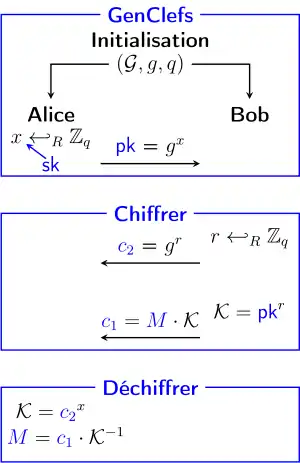
Comme il s'agit d'un schéma de chiffrement asymétrique, le cryptosystème est composé de trois algorithmes (probabilistes) : GenClefs, Chiffrer et Déchiffrer.
Pour l'illustration, on va considérer que Bob veut envoyer un message à Alice. Mais ce message contient des informations sensibles, Bob ne veut donc pas qu'il soit compréhensible par une autre personne qu'Alice. Ainsi Bob va chiffrer son message.
Comme les schémas de chiffrement asymétrique sont en règle générale plus lents que leurs analogues symétriques, le chiffrement ElGamal est souvent utilisé en pratique dans le cadre d'un chiffrement hybride, comme pour sa spécification PGP[2].
Une manière de voir ce schéma de chiffrement, est de faire un parallèle avec le protocole d’échange de clefs de Diffie-Hellman. L’algorithme de chiffrement consiste alors à envoyer un message chiffré par masque jetable sous la clef partagée , qui peut-être calculé par Alice vu qu’elle dispose de (voir illustration ci-contre).
Génération de clefs
La première étape du schéma de chiffrement consiste à produire une paire de clefs : la clef publique, et la clef secrète. La première servira à chiffrer les messages et la deuxième à les déchiffrer.
- Pour générer sa paire de clefs, Alice va commencer par prendre un groupe cyclique d’ordre q dans lequel le problème hypothèse décisionnelle de Diffie-Hellman est difficile, ainsi qu'un générateur de ce groupe.
- Alice va ensuite tirer un élément qui va être sa clef privée, et va calculer .
- Pour terminer, Alice va publier comme étant sa clef publique.
Algorithme de Chiffrement
Bob a donc accès à la clef publique d'Alice : . Pour chiffrer un message encodé comme un élément du groupe , Bob commence par tirer un aléa et va l'utiliser pour couvrir le message en calculant . Pour permettre à Alice de déchiffrer le message, Bob va adjoindre à cette partie du message une information sur l'aléa : .
Enfin le chiffré sera composé de ces deux morceaux : , et Bob envoie à Alice.
Algorithme de Déchiffrement
Ayant accès à et à , Alice peut ainsi calculer :
Et est donc en mesure de retrouver le message .
Sécurité
Face aux attaques à texte clair choisi
En observant les informations publiques : ; on se rend compte que seuls des éléments de sont rendus visibles et non pas les exposants (ici x et s respectivement). Informellement on peut remarquer que le problème du logarithme discret peut s'interpréter comme le fait qu'il est difficile de retrouver les informations secrètes ( par exemple) qui permettraient de retrouver le message.
De manière plus précise, c'est le problème de décision de Diffie-Hellmann (ou DDH) qui permet de garantir la sécurité sémantique du schéma.
Face aux attaques à chiffré choisi
Dans des modèles avec un attaquant possédant plus de puissance, comme sous attaques à chiffrés choisis, le cryptosystème d'ElGamal n'est pas sûr en raison de sa malléabilité ; en effet, étant donné un chiffré pour le message , on peut construire le chiffré , qui sera valide pour le message .
Cette malléabilité (il s’agit d’un homomorphisme multiplicatif) en revanche permet de l'utiliser pour le vote électronique par exemple[6].
Il existe cependant des variantes qui atteignent la sécurité face aux attaques à chiffrés choisis, comme le cryptosystème de Cramer-Shoup qui peut être vu comme une extension du chiffrement ElGamal.
Exemple
Pour l'exemple, on peut prendre le groupe , avec comme générateur g=5 (Mise en garde: ce n'est pas un groupe sûr, ces valeurs ont été prises uniquement pour produire un exemple simple).
Une clef publique possible pourrait donc être: , et comme clef secrète .
On remarquera que comme le chiffrement est un algorithme probabiliste, il y a différentes sorties possibles pour le même message. Un chiffré possible pour le message 42 pourrait donc être (58086963, 94768547), mais aussi (83036959, 79165157) pour les aléas r valant 6689644 et 83573058 respectivement.
Néanmoins, si on fait le calcul pour nos deux chiffrés, on obtiendra bien 42 en sortie.
Notes et références
- ElGamal 1984.
- RFC4880, (en) « OpenPGP Message Format »
- Journal des modifications de GnuPG 2.1
- Joux et Nguyen 2003.
- Katz et Lindell 2014, Chapitre 10.5 The ElGamal Encryption Scheme.
- Belenios, (en) « Spécifications de Belenios »
Annexes
Bibliographie
- [ElGamal 1984] (en) Taher ElGamal, « A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms », Crypto, Springer, (DOI 10.1007/3-540-39568-7_2, lire en ligne)
- [Katz et Lindell 2014] (en) Jonathan Katz et Yehuda Lindell, Introduction to Modern Cryptography, 2nd Edition, Boca Raton, Chapman and Hall, , 583 p. (ISBN 978-1-4665-7026-9, lire en ligne), « Chapitre 10.5 The El Gamal Encryption Scheme »
- [Menezes, van Oorschot et Vanstone 1996] (en) A. J. Menezes, P. C. van Oorschot et S. A. Vanstone, Handbook of Applied Cryptography, CRC Press, , 810 p. (ISBN 978-1-4398-2191-6, lire en ligne [PDF]), « Chapitre 8.4 ElGamal public-key encryption »
- [Joux et Nguyen 2003] (en) Antoine Joux et Kim Nguyen, « Separating Decision Diffie–Hellman from Computational Diffie–Hellman in Cryptographic Groups », Journal of Cryptology, vol. 16, , p. 239-247 (DOI 10.1007/s00145-003-0052-4)






























![{\displaystyle {\begin{aligned}{\textrm {Adv}}^{DDH}({\mathcal {B}})&=|\Pr[{\mathcal {B}}\to 1\mid {\text{DDH}}]-\Pr[{\mathcal {B}}\to 1\mid {\text{Aleatoire}}]|\\&=|\Pr[{\mathcal {A}}\to i\mid {\text{DDH}}]-\Pr[{\mathcal {A}}\to i\mid {\text{Aleatoire}}]|\\&=|\Pr[{\mathcal {A}}\to 0\mid i=0\land {\text{DDH}}]\Pr[i=0]+\Pr[{\mathcal {A}}\to 1\mid i=1\land {\text{DDH}}]\Pr[i=1]-{\frac {1}{2}}|\\&=|{\frac {1}{2}}(1-\Pr[{\mathcal {A}}\to 1\mid i=0\land {\text{DDH}}]+\Pr[{\mathcal {A}}\to 1\mid i=1\land {\text{DDH}}])-{\frac {1}{2}}|\\&={\frac {1}{2}}|-\Pr[{\mathcal {A}}\to 1\mid i=0\land {\text{DDH}}]+\Pr[{\mathcal {A}}\to 1\mid i=1\land {\text{DDH}}]|\\&={\frac {1}{2}}{\textrm {Adv}}^{\text{ElGamal}}({\mathcal {A}})\\&={\frac {\varepsilon }{2}}\end{aligned}}}](https://img.franco.wiki/i/ce2fad47e8bdaa6aa32052c032e6e31781d66bcb.svg)





