Oracle (machine de Turing)

En théorie de la complexité ou de la calculabilité, les machines de Turing avec oracle sont une variante des machines de Turing disposant d'une boîte noire, un oracle, capable de résoudre un problème de décision en une seule opération élémentaire. En particulier, l'oracle peut résoudre en temps constant un problème indécidable comme le problème de l'arrêt. Les machines de Turing avec oracle servent notamment à définir la hiérarchie polynomiale ou la hiérarchie arithmétique[1].

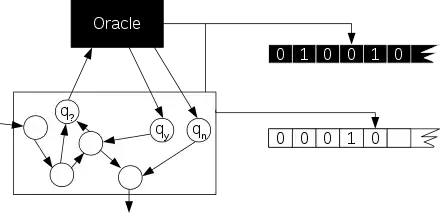
Une machine de Turing avec oracle peut faire appel à une boîte noire (oracle).

Approche intuitive

Une machine de Turing avec oracle se fait aider par un oracle. L'oracle peut être vu comme un dieu (il vaut mieux ne pas le considérer comme une machine) qui est capable de résoudre un certain problème de décision en un temps constant. Autrement dit, on donne une instance de ce problème entrée à l'oracle et il donne la réponse en un temps constant indépendant de la taille de la question. Ce problème peut être dans n'importe quelle classe de complexité. On peut même imaginer un oracle résolvant des problèmes qu'aucune machine de Turing ne sait résoudre, c'est-à-dire un problème indécidable comme le problème de l'arrêt.

Les oracles sont des outils purement théoriques, puisque ce modèle évite soigneusement de soulever la question de leur fonctionnement.

Définition

Soit L un langage. Une machine de Turing avec oracle L est une machine de Turing à plusieurs rubans avec un ruban de travail habituellement mais également dotée d'un ruban spécial, le ruban d'oracle, et de trois états particuliers, $q_{?}$ , $q_{y}$ et $q_{n}$ . Pour consulter l'oracle, la machine écrit un mot sur ce ruban, puis entre dans l'état $q_{?}$ . L'oracle décide alors en une étape de calcul si l'état suivant est $q_{y}$ ou $q_{n}$ , selon que ce mot fait partie ou non du langage L.

La machine peut consulter plusieurs fois l'oracle. On remarque qu'une même machine peut fonctionner avec différents oracles ; le langage reconnu sera alors a priori différent.

Classes de complexité avec oracles

Notations

On note $A^{L}$ où A est une classe de complexité et L un langage, la classe des langages reconnus par un algorithme de classe A avec comme oracle le langage L. Par exemple, si P est la classe des problèmes décidées par une machine de Turing déterministe en temps polynomial, et SAT est l'ensemble des formules de la logique propositionnelle qui sont satisfiables (voir problème SAT), alors $P^{SAT}$ est la classe des problèmes solubles en temps polynomial en utilisant un oracle qui résout le problème SAT en temps constant.

On note encore $A^{C}$ , où A et C sont deux classes de complexité, la classe des langages reconnus par un algorithme de classe A avec un oracle dont le langage décidé appartient à la classe C. Il est prouvé que si L est un langage complet dans la classe C, alors $A^{L}=A^{C}$ . Comme SAT est NP-complet, $P^{SAT}=P^{NP}$ .

P et NP

Concernant les classes de complexité classiques, on a : $P^{P}=P$ , puisque l'on peut transformer une machine de Turing polynomiale avec oracle polynomial en une machine polynomiale sans oracle. Pour cela, il suffit de remplacer le ruban de l'oracle par la machine correspondant au langage oracle. On sait aussi que $NP\subseteq P^{NP}$ , mais la question de l'égalité est ouverte (voir l'article hiérarchie polynomiale).

Les oracles ont été utilisés pour étudier la question de savoir si P = NP :

Théorème (Baker, Gill, Solovay, 1975) : il existe un langage A tel que $P^{A}=NP^{A}$ et il existe un langage B tel que $P^{B}\neq NP^{B}$ .

L'existence du langage A est assez facile à établir : il suffit de prendre un oracle assez puissant pour que la différence de puissance de calcul entre P et NP soit gommée. En fait, tout langage PSPACE-complet convient. En revanche, l'existence du langage B est remarquable. Elle ne permet cependant pas de trancher au sujet de savoir si P = NP : on peut imaginer que les modèles de calcul de la machine de Turing déterministe et non déterministe ont même puissance en temps polynomial, mais que l'un tire mieux parti de l'oracle B que l'autre.

Il est aussi possible de trouver un langage $I$ tel que la propriété $P^{I}=NP^{I}$ soit indécidable.

Autres résultats

Valiant et Vazirani ont démontré[2] que $NP\subseteq RP^{USAT}$ où USAT est le problème SAT, où on promet que la formule booléenne en entrée n'admet au plus qu'une solution. L'oracle à USAT fonctionne comme suit : il répond positivement sur des formules qui ont exactement une unique solution, il répond négativement sur des formules sans solution, et il répond de manière arbitraire sur les autres formules.

Le théorème de Toda utilise aussi la notion d'oracle.

Notes et références

Voir exercice 3.4.9 p. 68 dans Computational Complexity de C. Papadimitriou.
L. G. Valiant et V. V. Vazirani, « NP is as easy as detecting unique solutions », Theoretical Computer Science, vol. 47,‎ 1^er janvier 1986, p. 85–93 (ISSN 0304-3975, DOI 10.1016/0304-3975(86)90135-0, lire en ligne, consulté le 11 juillet 2019)

Bibliographie

(en) Christos Papadimitriou, Computational Complexity, Addison-Wesley, 1993 (ISBN 978-0-201-53082-7) Section 14.3 : « Oracles », p. 339 – 343.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.