Cryptographie symétrique
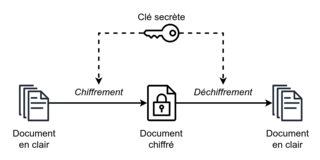
La cryptographie symétrique, également dite à clé secrète (par opposition à la cryptographie asymétrique), est la plus ancienne forme de chiffrement. Elle permet à la fois de chiffrer et de déchiffrer des messages à l'aide d'un même mot clé. On a des traces de son utilisation par les Égyptiens vers 2000 av. J.-C. Plus proche de nous, on peut citer le chiffre de Jules César, dont le ROT13 est une variante.
Clé et sécurité
L'un des concepts fondamentaux de la cryptographie symétrique est la clé. Une clé est une donnée qui (traitée par un algorithme) permet de chiffrer et de déchiffrer un message. Toutes les méthodes de chiffrement n'utilisent pas de clé. Le ROT13, par exemple, n'a pas de clé. Quiconque découvre qu'un message a été codé avec cet algorithme peut le déchiffrer sans autre information. Une fois l'algorithme découvert, tous les messages chiffrés par lui deviennent lisibles.
Si l'on modifiait le ROT13 en rendant le décalage variable, alors la valeur de ce décalage deviendrait une clé, car il ne serait plus possible de chiffrer et déchiffrer sans elle. L'ensemble des clés possibles comporterait alors 25 décalages (26 décalages si l'on considère le décalage nul).
Cet exemple montre le rôle et l'importance de la clé dans un algorithme de chiffrement ; et les restrictions qu'elle implique. Auguste Kerckhoffs (La Cryptographie militaire, 1883) énonce le principe de Kerckhoffs : pour être sûr, l'algorithme doit pouvoir être divulgué. En outre, il faut aussi que la clé puisse prendre suffisamment de valeurs pour qu'une attaque exhaustive — essai systématique de toutes les clés — soit beaucoup trop longue pour être menée à bien. Cela s'appelle la sécurité calculatoire.
Cette sécurité calculatoire s'altère avec le progrès technique, et la puissance croissante des moyens de calcul la fait reculer constamment. Exemple : le DES, devenu obsolète à cause du trop petit nombre de clés qu'il peut utiliser (pourtant 256). Actuellement, 280 est un strict minimum. À titre indicatif, l'algorithme AES, dernier standard d'algorithme symétrique choisi par l'institut de standardisation américain NIST en , utilise des clés dont la taille est, pour l'une de ses versions, de 128 bits, autrement dit il y en a 2128. Pour donner un ordre de grandeur sur ce nombre, cela fait environ 3,4 × 1038 clés possibles ; l'âge de l'univers étant de 1010 années, si on suppose qu'il est possible de tester 1 000 milliards de clés par seconde (soit 3,2 × 1019 clés par an), il faudra encore plus d'un milliard de fois l'âge de l'univers. Dans un tel cas, on pourrait raisonnablement penser que notre algorithme est sûr, du moins tant qu'il n'y a pas de meilleure attaque que celle par force brute.
Cette notion de sécurité calculatoire pose la question de la sécurité absolue. On sait depuis Claude Shannon et son article Communication theory of secrecy system (1949) que le chiffrement de Gilbert Vernam qui consiste à ajouter au message en clair une clé de la même longueur (voir XOR) est parfaitement sûr. C'est le seul pour lequel nous soyons capables de prouver une telle chose. L'inconvénient est que pour chiffrer un message de n bits, il faut au préalable avoir échangé une clé de n bits avec le destinataire du message, et cela par une voie absolument sûre, sinon chiffrer devient inutile. Très peu de cas nécessitent un tel système, mais c'était toutefois le système utilisé pour le Téléphone rouge entre le Kremlin et la Maison-Blanche.
Petite taxinomie du chiffrement symétrique classique
Jusqu'aux communications numériques, les systèmes utilisaient l'alphabet et combinaient substitutions — les symboles sont changés mais restent à leur place — et transpositions — les symboles ne sont pas modifiés mais changent de place.
La substitution est dite monoalphabétique quand l'algorithme de codage n'utilise aucun autre paramètre que la lettre à coder, de sorte qu'une lettre est toujours remplacée par la même lettre (relation 1→1). C'est le cas d'un algorithme à décalage simple. Quand l'algorithme de codage utilise un ou plusieurs autres paramètres (ex : sa position dans le message), chaque lettre à coder peut alors être remplacée par plusieurs lettres différentes selon les cas (relation 1→n). On parle alors de substitution polyalphabétique — e.g. le chiffre de Vigenère, Enigma.
La substitution peut utiliser la méthode du décalage, où chaque lettre est transformée en la lettre n positions plus loin dans l'alphabet, en rebouclant, c’est-à-dire la lettre suivant 'z' est 'a'. On parle de décalage simple — est également connu sous le nom de chiffre de Jules César- quand le décalage est identique pour toutes les lettres du message. Avec le chiffre de Blaise de Vigenère, on applique un nombre quelconque n de décalages, le premier décalage est utilisé pour chiffrer la lettre numéro 1, puis la 1+n, 1+2n, … le second décalage pour la lettre numéro 2, 2+n, 2+2n, … Usuellement, la valeur de ces décalages est donnée par un mot de longueur n dont la ie lettre donne la valeur du ie décalage. Clarifions par un exemple.
Message clair : wikipedia Mot clé : crypto Message chiffre : yzixisfzy
Un 'a' dans le mot clé correspond à un décalage de 0, un 'b' à un décalage de 1, etc. Dans notre exemple, la clé a 6 lettres, donc les lettres 1 ('w') et 7 ('d') sont chiffrées par le même décalage, à savoir 2.
La machine Enigma utilisée par les Allemands durant la Seconde Guerre mondiale est également basée sur les substitutions, mais avec un mécanisme beaucoup plus sophistiqué.
Une autre forme de la substitution est le dictionnaire : au lieu de changer les symboles du message un à un, ce sont des mots entiers que l'on remplace.
Pour les transpositions on modifie l'ordre des symboles du texte clair. Une technique consiste à se donner un mot clé, à écrire le message sous ce mot clé et à lire le texte en colonne, par ordre alphabétique.
Message : wikipediaestuneencyclopedielibre Mot clé : crypto
on écrit sous wikipe
le mot clé diaest
uneenc
yclope
dielib
re****
lettre du mot clé (ordre alphabétique) coprty
on ordonne les weiipk
colonnes dteisa
ucenne
yeocpl
dbliie
r**e**
Message chiffré : wduydr etceb* ieeol* iincie psnpi* kaele*
Les astérisques sont ajoutés pour le déchiffrement et les espaces dans le message chiffré uniquement pour la lisibilité. Le message, s'il était par exemple envoyé à un destinataire qui connaît le mot clé, serait le suivant :
Message chiffré : wduydretceb*ieeol*iinciepsnpi*kaele*
Techniques modernes
Depuis l'avènement du numérique, les paradigmes du chiffrement symétrique ont bien changé. D'une part, la discipline s'est formalisée, même si la conception de système de chiffrement garde inévitablement un aspect artisanal. En effet dans ce domaine, la seule chose que l'on sache prouver est la résistance face à des types d'attaques connues. D'autre part, la forme du texte chiffré ayant changé, les méthodes ont suivi. Les algorithmes modernes chiffrent des suites de bits.
On distingue deux types d'algorithmes, les algorithmes en blocs, qui prennent bits en entrée et en ressortent , et les algorithmes à flots, qui chiffrent bit par bit sur le modèle du chiffre de Vernam. Dans ce dernier cas, l'algorithme engendre une suite de bits qui est ajouté (cf. XOR) à la suite binaire à chiffrer. Les techniques utilisées pour générer la suite que l'on ajoute -- appelée la suite chiffrante -- sont diverses. Elles peuvent utiliser des registres à décalage à rétroaction linéaire, composés de façon non linéaire (par exemple A5/1 ou E0, mais pas RC4 qui est ou a été très répandu) ... ou utiliser un chiffrement par bloc en mode avec un mode opératoire adapté.
La seconde famille d'algorithmes, ceux en blocs, est en général construite sur un modèle itératif. Ce modèle utilise une fonction qui prend une clé et un message de bits. C'est cette fonction qui est itérée un certain nombre de fois, on parle de nombre de tours. À chaque tour, la clé utilisée est changée et le message que l'on chiffre est le résultat de l'itération précédente.
- ;
- ;
- …
- ;
Les clés utilisées sont déduites d'une clé maître qui est la quantité secrète que doivent partager émetteur et destinataire. L'algorithme générant ces clés à partir de est appelé l'algorithme de cadencement de clés.
Pour qu'un tel système puisse fonctionner, la fonction utilisée doit être injective par rapport à pour un fixé, c'est-à-dire qu'il faut pour toute clé et message pouvoir recalculer à partir de , autrement le déchiffrement n'est pas possible et par conséquent on ne dispose pas d'un algorithme utilisable. Formellement, cela signifie qu'il existe une fonction vérifiant
- .
La sécurité d'un tel système repose essentiellement sur deux points : l'algorithme de cadencement de clé, et la robustesse de la fonction . Si l'algorithme de cadencement est mal conçu, les peuvent être déductibles les unes des autres, ou mal réparties, etc. Dire de la fonction qu'elle est robuste signifie qu'on la suppose difficile à inverser sans connaître la clé ayant servi dans le calcul de . La propriété qui garantit cela est que soit une fonction pseudo-aléatoire, c'est-à-dire qu'il n'existe pas de méthode efficace pour distinguer l'ensemble des sorties possibles de cette fonction de celles d'une fonction dont la sortie est générée aléatoirement. Une condition nécessaire pour cela est que soit surjective; sinon, il existe des éléments de l'ensemble d'arrivée qui peuvent forcément être généré aléatoirement, mais pas par . Comme on a vu infra que est aussi injective par nécessité de pouvoir déchiffrer (existence de ), c'est nécessairement une bijection, autrement dit, une permutation (puisque son ensemble de départ est le même que son ensemble d'arrivée).
En d'autres termes, quand est une fonction pseudo-aléatoire, si on connaît seulement , et , on ne peut pas retrouver le message , si ce n'est en effectuant une recherche exhaustive de la clé , c'est-à-dire en calculant
- 1) ) ;
- 2) ;
et cela pour toutes les clés jusqu'à ce que l'on en trouve une pour laquelle est égal à . On est alors assuré d'avoir le message qui n'est autre que . Le problème étant que si est constitué de bits, il faut en moyenne essais. En prenant assez grand, on peut être sûr que cela n'est pas réalisable en pratique : supposons que l'on puisse essayer 109 (un milliard) clés par seconde, soit environ 230, il y a 31 557 600 secondes par an, soit 225, en conséquence on peut tester 255 clés par an. Si on prend pour une valeur de 80 bits, il faudrait 224 ans, plus de 16 millions d'années.
Une technique très répandue pour fabriquer des fonctions est celle du schéma de Feistel. Dans ce schéma, le message à chiffrer est découpé en 2 blocs de n2 bits, et le message chiffré est
où le '⊕' est le XOR et est une fonction quelconque, on n'a plus à supposer que c'est une permutation. En effet, on peut retrouver à partir de la clé
- 1) connaissant , on connaît qui est sa partie gauche,
- 2) on calcule ,
- 3) on ajoute le résultat du calcul précédent à la partie droite de , et on retrouve ,
cela sans restriction sur . Clairement, dans ce schéma, la robustesse de repose sur la fonction .

























