En cryptographie, le chiffrement par décalage, aussi connu comme le chiffre de César ou le code de César (voir les différents noms), est une méthode de chiffrement très simple utilisée par Jules César dans ses correspondances secrètes (ce qui explique le nom « chiffre de César »).
Le texte chiffré s'obtient en remplaçant chaque lettre du texte clair original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Pour les dernières lettres (dans le cas d'un décalage à droite), on reprend au début. Par exemple avec un décalage de 3 vers la droite, A est remplacé par D, B devient E, et ainsi jusqu'à W qui devient Z, puis X devient A etc. Il s'agit d'une permutation circulaire de l'alphabet. La longueur du décalage, 3 dans l'exemple évoqué, constitue la clé du chiffrement qu'il suffit de transmettre au destinataire — s'il sait déjà qu'il s'agit d'un chiffrement de César — pour que celui-ci puisse déchiffrer le message. Dans le cas de l'alphabet latin, le chiffre de César n'a que 26 clés possibles (y compris la clé nulle, qui ne modifie pas le texte).
Il s'agit d'un cas particulier de chiffrement par substitution monoalphabétique : ces substitutions reposent sur un principe analogue, mais sont obtenues par des permutations quelconques des lettres de l'alphabet. Dans le cas général, la clé est donnée par la permutation, et le nombre de clés possibles est alors sans commune mesure avec celui des chiffrements de César.
Le chiffrement de César a pu être utilisé comme élément d'une méthode plus complexe, comme le chiffre de Vigenère. Seul, il n'offre aucune sécurité de communication, à cause du très faible nombre de clés, ce qui permet d'essayer systématiquement celles-ci quand la méthode de chiffrement est connue, mais aussi parce que, comme tout encodage par substitution monoalphabétique, il peut être très rapidement « cassé » par analyse de fréquences (certaines lettres apparaissent beaucoup plus souvent que les autres dans une langue naturelle).
Exemple
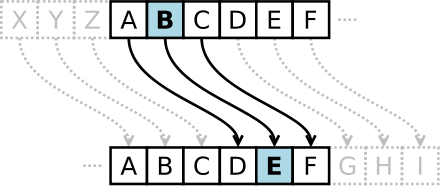
Le chiffrement peut être représenté par la superposition de deux alphabets, l'alphabet clair présenté dans l'ordre normal et l'alphabet chiffré décalé, à gauche ou à droite, du nombre de lettres voulu. Nous avons ci-dessous l'exemple d'un encodage de 3 lettres vers la droite. Le paramètre de décalage (ici 3) est la clé de chiffrement :
clair : ABCDEFGHIJKLMNOPQRSTUVWXYZ chiffré : DEFGHIJKLMNOPQRSTUVWXYZABC
Pour encoder un message, il suffit de regarder chaque lettre du message clair, et d'écrire la lettre encodée correspondante. Pour déchiffrer, on fait tout simplement l'inverse.
original : WIKIPEDIA L'ENCYCLOPEDIE LIBRE encodé : ZLNLSHGLD O'HQFBFORSHGLH OLEUH
Le chiffrement peut aussi être représenté en utilisant les congruences sur les entiers. En commençant par transformer chaque lettre en un nombre (A = 0, B = 1, etc., Z = 25)[1], pour encoder une lettre avec une clé n il suffit d'appliquer la formule[2] :
Le déchiffrement consiste à utiliser la clé opposée ( à la place de ) :
On peut s'arranger pour que le résultat soit toujours représenté par un entier de 0 à 25 : si (respectivement ) n'est pas dans l'intervalle , il suffit de soustraire (respectivement ajouter) 26.
Le décalage demeurant toujours le même pour un même message, cette méthode est une substitution monoalphabétique, contrairement au chiffre de Vigenère qui constitue une substitution polyalphabétique.
Dénominations
Le chiffrement par décalage possède plusieurs synonymes :
- le chiffre de César. César utilisait pour ses correspondances un chiffrement par décalage de 3 lettres vers la droite. Aujourd'hui l'expression « chiffre de César » désigne n'importe quel chiffrement par décalage, pas forcément de 3[3] ;
- le code de César.
Historique

César
Postérieur et plus simple que la scytale[4], le chiffre de César doit son nom à Jules César qui, selon Suétone l'utilisait avec l'alphabet grec (inintelligible pour la plupart des Gaulois mais langue maîtrisée par les élites dirigeantes romaines[5]) et un décalage de trois sur la droite pour certaines de ses correspondances secrètes, notamment militaires :
« Il y employait, pour les choses tout à fait secrètes, une espèce de chiffre qui en rendait le sens inintelligible (les lettres étant disposées de manière à ne pouvoir jamais former un mot), et qui consistait, je le dis pour ceux qui voudront les déchiffrer, à changer le rang des lettres dans l'alphabet, en écrivant la quatrième pour la première, c'est-à-dire le d pour le a, et ainsi de suite[6]. »
— Suétone, Vie des douze Césars, Livre I, paragraphe 56.
Aulu-Gelle confirme l'usage par Jules César de méthodes de chiffrement par substitution :
« Nous avons un recueil des lettres de J. César à C. Oppius et Balbus Cornelius, chargés du soin de ses affaires en son absence. Dans ces lettres, on trouve, en certains endroits, des fragments de syllabes sans liaison, caractères isolés, qu'on croirait jetés au hasard : il est impossible d'en former aucun mot. C'était un stratagème dont ils étaient convenus entre eux : sur le papier une lettre prenait la place et le nom d'une autre ; mais le lecteur restituait à chacune son nom et sa signification »
— Aulu-Gelle, Nuits attiques, livre XVII, 9
Bien que César soit le premier personnage connu à utiliser cette technique, on sait que d'autres chiffres par substitution, éventuellement plus complexes, ont été utilisés avant lui, et il n'est donc pas certain qu'il soit le premier à l'avoir conçu, même s'il a pu le réinventer[7].
Auguste, son neveu, utilisait aussi un chiffre, consistant en un décalage de un sans boucler à la fin de l'alphabet :
« Lorsqu'il écrivait en chiffres, il employait le b pour a, le c pour le b, et ainsi de suite pour les autres lettres. Au lieu du z il mettait deux a. »
Toujours suivant les écrits d'Aulu-Gelle, on peut penser que Jules César utilisait d'autres clés, et même d'autres techniques de chiffrement plus complexes[8]. En particulier Aulu-Gelle fait référence à un traité (aujourd’hui perdu) consacré aux chiffres utilisés par César[9].
On ignore quelle était l'efficacité du chiffre de César à son époque. La première trace de techniques de cryptanalyse date du IXe siècle avec le développement dans le monde arabe de l'analyse fréquentielle[10].
Utilisations
Un chiffre de César, avec un décalage de un, apparaît au dos du Mezuzah[11].
Au XIXe siècle, les pages d'annonces personnelles des journaux étaient parfois utilisées pour la transmission de messages chiffrés à l'aide de codes simples. David Kahn donne des exemples d'amants communiquant de manière confidentielle en chiffrant leurs messages à l'aide du chiffre de César dans le quotidien britannique The Times[12]. Le chiffre de César fut encore employé en 1915 : l'armée russe le préférait à d'autres codes plus élaborés mais qui s'étaient révélés trop difficiles d'utilisation pour leurs troupes ; les analystes allemands et autrichiens eurent peu de mal à déchiffrer leurs messages[13].
Utilisations modernes
Aujourd'hui, on peut trouver le chiffre de César dans des jouets promotionnels pour enfants. Les livres-jeu emploient souvent cette méthode, avec un décalage de un ou deux dans un sens ou dans l'autre, pour donner des indications sans rendre le jeu trop facile.
Plusieurs cas particuliers ont été nommés par jeux de mots : « avocat » (A vaut K), « cassis » (K 6) et « cassette » (K 7). Typiquement, un jeu pour enfant peut impliquer de décoder un message, en donnant un indice contenant le mot « avocat ».
Un tel code avec un décalage de 13 caractères est aussi employé dans l'algorithme ROT13 : cette méthode très simple est utilisée dans certains forums sur Internet pour brouiller tout ou partie d'un texte (comme la chute d'une blague, ou un spoiler), mais pas comme méthode de chiffrement en tant que tel[14].
En , le chef en fuite de la mafia Bernardo Provenzano a été capturé en Sicile grâce notamment au déchiffrement d'une partie de sa correspondance qui utilisait une variante du chiffrement de César basée sur les nombres : A s'écrivait 4, B 5, etc[15].
Attaques
| Décalage du déchiffrement |
Texte de test |
|---|---|
| 0 | GVCTX SKVEQ QI |
| 1 | FUBSW RJUDP PH |
| 2 | ETARV QITCO OG |
| 3 | DSZQU PHSBN NF |
| 4 | CRYPT OGRAM ME |
| 5 | BQXOS NFQZL LD |
| 6 | APWNR MEPYK KC |
| … | |
| 23 | JYFWA VNYHT TL |
| 24 | IXEVZ UMXGS SK |
| 25 | HWDUY TLWFR RJ |
Le chiffre de César peut être cassé très facilement, même à l'aide du seul texte chiffré. On peut distinguer deux cas :
- le cryptanalyste a connaissance du fait qu'un simple chiffrement par substitution a été employé, mais ignore qu'il s'agit du chiffre de César en particulier ;
- le cryptanalyste sait que le chiffre de César a été utilisé, mais ignore la valeur du décalage.
Par recherche de la méthode de chiffrement
Dans le premier cas, il est possible de casser le chiffre de César à l'aide des mêmes techniques que dans le cas général d'un chiffrement par substitution, à savoir l'analyse fréquentielle ou la recherche de mots probables[16]. Lors de la résolution, le cryptanalyste ne sera pas sans remarquer une certaine régularité dans les décalages, et en déduira que l'algorithme employé est le chiffre de César.
Par recherche de la valeur du décalage
Dans le deuxième cas, comme il n'y a qu'un nombre limité de décalages (vingt-six dont un inutile), il suffit de tester tous les chiffrements possibles jusqu'à trouver le bon. C'est ce qu'on appelle une attaque par force brute, technique de test de toutes les combinaisons possibles[17]. Une méthode simple pour mener l'attaque est de prendre un fragment du texte chiffré et d'écrire dans un tableau tous les décalages possibles (voir le tableau ci-contre)[18]. Dans ce tableau, on a pris le fragment GVCTX SKVEQ QI ; le texte en clair apparaît ainsi facilement à la quatrième ligne. Une autre façon de procéder serait d'écrire toutes les lettres de l'alphabet, en dessous de chaque lettre du fragment, et en commençant par celle-ci. Ce genre d'attaque peut être accélérée en utilisant des bandes avec l'alphabet écrit dessus ; les bandes étant placées en colonne sur le texte chiffré (lettre sur lettre : par exemple, le « E » de la bande doit être placé au-dessus du « E » du texte chiffré), la phrase en clair doit apparaître sur une des lignes.
Analyse fréquentielle
Une autre attaque possible est de faire une analyse de fréquence d'apparition des lettres : on génère un graphique sur la fréquence d'apparition de chaque lettre dans le texte chiffré et un autre avec un texte de référence, dans la langue du message d'origine, et on explore par décalages successifs toutes les possibilités. En les comparant, un humain peut facilement voir la valeur du décalage entre ces deux graphiques, et trouver la clé de chiffrement. Cette technique s'appelle l'analyse fréquentielle. Par exemple, en anglais, les lettres E et T sont les plus fréquentes et les lettres Q et Z, les moins fréquentes[19]. Des ordinateurs peuvent aussi faire ce travail de reconnaissance en évaluant la concordance de distribution des deux textes (le texte chiffré et celui de référence) en utilisant, par exemple, une fonction test du χ² de Pearson[20].
Avec des textes longs, il est très probable qu'il n'y ait qu'une seule possibilité de déchiffrement. Mais pour de courts textes, il peut y avoir plusieurs possibilités de déchiffrement. Par exemple, « NYHCL » peut être déchiffré en « grave » (par un décalage de 19) ou en « tenir » (6) (pour un texte en français) ; ou alors « DQODG » peut donner « bombe » (24) ou « recru » (14) (voir aussi : distance d'unicité).
Composition de chiffrements
Enchaîner les chiffrements (et les déchiffrements) ne donne pas de protection supplémentaire car chiffrer un texte avec un décalage de trois sur la gauche, puis le chiffrer de nouveau avec un décalage de sept sur la droite revient exactement au même que de coder le texte de départ avec un décalage de quatre sur la droite (). En termes mathématiques, l'ensemble des vingt-six opérations de chiffrement (en comprenant le décalage nul c'est-à-dire le texte chiffré identique au texte clair) est stable par composition. Il forme même un groupe[21], puisque, de plus, une opération de déchiffrement est identique à une opération de chiffrement.
Le chiffre de Vigenère
Le chiffre de Vigenère utilise le chiffre de César mais avec un décalage différent suivant la position de la lettre décalée dans le texte ; la valeur de ce décalage est définie à l'aide d'un mot-clé, chaque lettre du mot-clé désigne le décalage correspondant à sa position dans l'alphabet (0 pour A, 1 pour B etc.). Si la longueur du mot clé est n, toutes les lettres du texte clair en position un multiple de n sont décalées suivant le même entier, de même pour celles en position un multiple de n plus 1, etc. L'utilisation de plusieurs décalages différents rend inopérante l'analyse fréquentielle classique, du moins directement. Des méthodes statistiques plus avancées, utilisant l'indice de coïncidence, permettent cependant de casser le code (voir aussi cryptanalyse du chiffre de Vigenère).
On peut voir le chiffrement de Vernam (ou « masque jetable ») comme un chiffre de Vigenère où le mot-clé est de même longueur que le texte à chiffrer, choisi de façon complètement aléatoire, et utilisé une seule fois. Il est alors théoriquement incassable, mais difficile à utiliser en pratique.
Notes et références
- (en) Dennis Luciano et Gordon Prichett, « Cryptology: From Caesar Ciphers to Public-Key Cryptosystems », The College Mathematics Journal, vol. 18, no 1, , p. 3 (DOI ) .
- R. Wobst, op. cit. Cryptology Unlocked p. 19.
- David Kahn, « To this day, any cipher alphabet that consists of the standard sequence, like Caesar's, is called a Caesar alphabet, even if it begins with a letter other than D. » dans The Codebreakers.
- Charles-François Vesin, La cryptographie dévoilée : ou, Art de traduire ou de déchiffrer toutes les écritures en quelque caractère et en quelque langue que ce soit ... appliqué aux langues française, allemande, anglaise, latine, italienne, espagnole, suivi d'un précis analytique des écrites ..., , 259 p. (lire en ligne) .
- Rémy Kauffer, Histoire mondiale des services secrets, Perrin, , p. 23 .
- (en) Texte en anglais.
- (en) Edgar C. Reinke, « Classical Cryptography », The Classical Journal, vol. 58, no 3, , p. 115 .
- (en) Edgar C. Reinke, « Classical Cryptography », The Classical Journal, vol. 58, no 3, , p. 114 et note 6 p 121.
« On trouve même un traité assez bien écrit du grammairien Probus au sujet de la signification cachée des lettres dans la correspondance de César. »
— Aulus Gellius, 17.9.1–5
, cité par Reinke, voir note précédente.- S. Singh, op. cit. The Code Book pp. 14-20.
- (en) Alexander Poltorak, « Mezuzah and Astrology - The Mysterious Name », sur http://www.chabad.org/ (consulté le ).
- D. Kahn, op. cit. The Codebreakers — The Story of Secret Writing pp. 775-776.
- D. Kahn, op. cit. The Codebreakers — The Story of Secret Writing pp. 631-632.
- R. Wobst, op. cit. Cryptology Unlocked p. 20.
- (en) John Leyden, « Mafia boss undone by clumsy crypto », The Register, (consulté le ).
- A. Beutelspacher, op. cit. Cryptology pp. 9-11.
- A. Beutelspacher, op. cit. Cryptology pp. 8-9.
- (en) Albert C. Leighton, « Secret Communication among the Greeks and Romans », Technology and Culture, vol. 10, no 2, , p. 153 (DOI ) .
- S. Singh, op. cit. The Code Book pp. 72-77.
- (en) Chris Savarese et Brian Hart, « The Caesar Cipher » (consulté le ).
- R. Wobst, op. cit. Cryptology Unlocked p. 31.
Voir aussi
Bibliographie
- (en) Friedrich L. Bauer, Decrypted Secrets, 2, (ISBN 3-540-66871-3)
- (en) Albrecht Beutelspacher (trad. de l'allemand), Cryptology : an introduction to the art and science of enciphering, encrypting, concealing, hiding and safeguarding, Washington (D.C.), Mathematical Association of America, , 156 p. (ISBN 0-88385-504-6, lire en ligne) .
- (en) David Kahn, The Codebreakers — The Story of Secret Writing, (ISBN 0-684-83130-9) .
- (en) Josef Pieprzyk, Thomas Hardjono et Jennifer Seberry, Fundamentals of Computer Security, Springer, , 677 p. (ISBN 3-540-43101-2, lire en ligne) .
- (en) Simon Singh, The Code Book, Anchor, , 411 p. (ISBN 0-385-49532-3) . Édition française sous le titre Histoire des codes secrets, Livre de Poche, 2001, (ISBN 2253150975)..
- (en) Abraham Sinkov et Paul L. Irwin, Elementary Cryptanalysis : A Mathematical Approach, New York, Mathematical Association of America, , 222 p. (ISBN 0-88385-622-0) .
- (en) Reinhard Wobst, Cryptology Unlocked, Chichester/Hoboken, NJ, Wiley, , 540 p. (ISBN 978-0-470-06064-3) .

![E_{n}(x){{=}}(x+n)\ [26]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bb7ce25808fa382897993e508e950e0a461e328)


![D_{n}(x){{=}}(x-n)\ [26]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5c73598b7e12ca3b6576b128c6afb88d8f81d2)


![[0,25]](https://wikimedia.org/api/rest_v1/media/math/render/svg/85d83a36d3ab8754e51aeed2b5451130f89f8d6a)

