Twofish
Twofish est un algorithme de chiffrement symétrique par bloc inventé et analysé par Bruce Schneier, Niels Ferguson, John Kelsey, Doug Whiting, David Wagner et Chris Hall[1].
| Concepteur(s) | Bruce Schneier, Niels Ferguson, John Kelsey, Doug Whiting, David Wagner et Chris Hall |
|---|---|
| Première publication | 2000 |
| Dérivé de | Blowfish |
| Chiffrement(s) basé(s) sur cet algorithme | Aucun |
| Taille(s) du bloc | 128 bits |
|---|---|
| Longueur(s) de la clé | 128, 192, 256 bits |
| Structure | schéma de Feistel, pseudo-transformation de Hadamard |
| Nombre de tours | 16 tours |
Meilleure cryptanalyse
Attaques sur des versions de 5, 6 et 7 tours.
Description
Twofish chiffre des blocs de 128 bits avec une clé de 128, 192 ou 256 bits. Il reprend en partie des concepts présents dans le populaire Blowfish, du même auteur[1]. Il était l'un des cinq finalistes du concours AES. mais il n'a pas été sélectionné pour le standard[2] - [3].
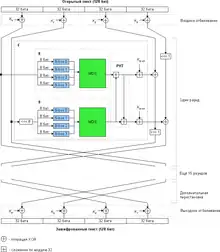
Les particularités de Twofish sont[1]:
- une préparation des clés internes relativement complexe
- un calcul des boîtes de substitution (S-Box) en fonction de la clé
- utilisation d'une diffusion efficace via la pseudo-transformation de Hadamard (PHT), celle-ci provient de la famille des chiffrements SAFER.
- utilisation d'un schéma de Feistel comme celui de DES avec 16 tours
Performances
Twofish a été conçu pour être implanté dans des cartes à puce et d'autres systèmes embarqués. Sur un Pentium, une implémentation optimisée en assembleur permet de chiffrer un bloc de 128 bits en 18,1 coups d'horloge[1].
Twofish est légèrement plus lent que Rijndael (gagnant du concours AES) mais plus rapide que les autres finalistes d'AES[4]. Il surpasse Rijndael avec une clé de 256 bits[2]. Toutefois, depuis que les concepteurs de puces électroniques ont créé le jeu d'instructions AES, Rijndael peut être beaucoup plus rapide que Twofish[5].
Cryptanalyse
En 2005, Bruce Schneier soulignait qu'aucune attaque n'avait jusque là pu casser la version complète de Twofish[6].Ses concepteurs ont publié des attaques sur des versions à 6 et 7 tours[7]. Une attaque sur 5 tours avec une complexité de 251 a également été proposée[8].
La recherche exhaustive reste le seul moyen pour le casser. Il semble plus résistant que ce qui avait été annoncé durant le concours AES. De par sa complexité, la cryptanalyse de cet algorithme reste délicate. Malgré ses atouts, il reste relativement peu utilisé et a été supplanté par le gagnant du concours AES[9].
Notes et références
- (en) B. Schneier, J. Kelsey, D. Whiting, D. Wagner, C. Hall et N. Ferguson, « Twofish: A 128-Bit Block Cipher », Schneier on Security,
- (en) Bruce Schneier et Doug Whiting, « A Performance Comparison of the Five AES Finalists », (consulté le )
- (en-US) Information Technology Laboratory Computer Security Division, « AES Development - Cryptographic Standards and Guidelines | CSRC | CSRC », sur CSRC | NIST, (consulté le )
- (en) Geoffrey Keating, « Performance analysis of AES candidates on the 6805 CPU core », Proceedings of the second AES Candidate Conference, , p. 109-114 (lire en ligne [PDF])
- (en-US) Scott Brown, « A Look at the Performance Impact of Hardware-Accelerated AES », sur Scott Brown Consulting, (consulté le )
- (en) Bruce Schneier, « Twofish Cryptanalysis Rumors - Schneier on Security », sur www.schneier.com (consulté le )
- « Academic: Impossible Differentials in Twofish - Schneier on Security », sur www.schneier.com (consulté le )
- (en) Shiho Moriai et Yiqun Lisa Lin, « Cryptanalysis of Twofish (II) » [PDF],
- (en) Matthew Green, « So you want to use an alternative cipher… », sur A Few Thoughts on Cryptographic Engineering, (consulté le )
Bibliographie
- Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, Chris Hall et Niels Ferguson, The Twofish Encryption Algorithm: A 128-Bit Block Cipher, New York, John Wiley & Sons, (ISBN 0-471-35381-7)
Liens externes
- (en) code de référence