Réseau de Feistel

Réseau de Feistel à n tours utilisant l'opérateur XOR

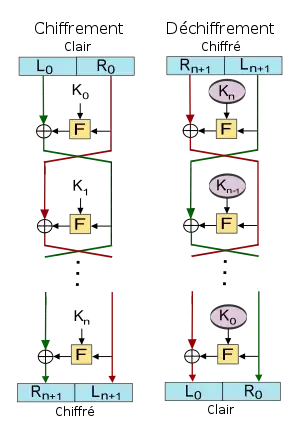
Un réseau de Feistel est subdivisé en plusieurs tours ou étages. Dans sa version équilibrée, le réseau traite les données en deux parties de taille identique. À chaque tour, les deux blocs sont échangés puis un des blocs est combiné avec une version transformée de l'autre bloc. Pour simplifier, la moitié des données sont encodées avec la clef, puis le résultat de cette opération est ajouté grâce à un xor (ou exclusif) à l'autre moitié des données. Puis au tour suivant, on inverse : c'est au tour de la dernière moitié d'être chiffrée puis d'être ajoutée avec un xor à la première moitié, sauf qu'on utilise les données chiffrées précédemment (sinon ça ne servirait à rien de faire plus de deux tours). Le schéma ci-contre montre le cheminement des données (le ⊕ représente le xor). Chaque tour utilise une clé intermédiaire, en général tirée de la clé principale via une génération appelée key schedule. Les opérations effectuées pendant le chiffrement avec ces clefs intermédiaires sont spécifiques à chaque algorithme.

Dans le cas de DES, le réseau de Feistel possède 16 tours, chacun avec une sous-clé. Ces différentes clés permettent d'améliorer la robustesse d'un algorithme face à la cryptanalyse.

Une variante, le réseau de Feistel non-équilibré coupe les données en deux parties de tailles différentes. Cette variante a été utilisée dans MacGuffin de Bruce Schneier, ou encore Skipjack, candidat pour AES.

Une définition formelle d'un réseau de Feistel peut être donnée sous plusieurs formes. Nous reprenons ici la notation utilisée par Knudsen dans Partial and Higher Order Differentials and Applications to DES.

${\displaystyle C_{0}^{L}=P^{L}~}$ et ${\displaystyle C_{0}^{R}=P^{R}~}$

${\displaystyle C_{i}=(C_{i}^{L},C_{i}^{R})=(C_{i-1}^{R},f(C_{i-1}^{R},K_{i})+C_{i-1}^{L})~}$

${\displaystyle C^{L}=C_{r}^{L}~}$ et ${\displaystyle C^{R}=C_{r}^{R}~}$

• l'exposant représente la sous-partie du bloc considérée (L à gauche, R à droite).
• ${\displaystyle P~}$ correspond au bloc de texte clair, ${\displaystyle P_{i}^{L}}$ correspond au bloc de gauche à l'entrée du tour ${\displaystyle i~}$
• ${\displaystyle C~}$ correspond au bloc de texte chiffré, ${\displaystyle C_{i}^{R}}$ correspond au bloc de droite à la sortie du tour ${\displaystyle i~}$
• ${\displaystyle K_{i}~}$ est la clé du tour ${\displaystyle i~}$, elle est calculée grâce à un key schedule de la clé principale
• ${\displaystyle r~}$ est le nombre de tours dans l'algorithme
• ${\displaystyle +~}$ est une opération dans un groupe commutatif (souvent un XOR ou une addition)

Les schémas de Feistel ont été largement analysés et examinés par les experts. Plusieurs attaques sont possibles mais les deux principales sont :

• la cryptanalyse linéaire;
• la cryptanalyse différentielle.

Ces méthodes ont fait leur preuve sur DES et sur d'autres algorithmes similaires. Mais cela ne signifie pas que l'utilisation d'un réseau de Feistel va obligatoirement entraîner des vulnérabilités significatives. Grâce à l'ajout de différentes techniques et avec une conception bien menée, on peut considérablement améliorer la résistance d'un algorithme basé sur Feistel. C'est le cas pour Blowfish qui est cryptographiquement sûr à la date de décembre 2008.

En général, les cryptanalystes s'attaquent en premier à des versions amoindries des chiffrements, c’est-à-dire comportant moins de tours.

Un grand nombre d'algorithmes utilise des réseaux de Feistel, avec des variantes. Voici une liste non exhaustive :

• DES
• Blowfish
• Twofish
• Camellia
• SEED
• RC5
• OAEP
• TEA