Arbre (théorie des graphes)

Un graphe représente un ensemble de points, appelés sommets ou nœuds, reliés ou non entre eux par des traits, appelés arêtes.

Il s'agit donc d'un concept très simple et d'un outil de modélisation très général, utile dans de nombreux domaines.

• Par exemple une carte routière peut être modélisée par un graphe : les villes sont les sommets et on reliera deux sommets par un trait si et seulement si les villes qu'ils représentent ont une route les connectant directement.
• Un réseau social est un autre exemple : les utilisateurs sont les sommets et on reliera deux utilisateurs si et seulement s'ils sont chacun ami avec l'autre.

À noter que la disposition des sommets (position dans l'espace) n'a pas d'importance, ni même la forme des arêtes reliant éventuellement ces sommets (ligne droite, courbe etc). La seule chose qui compte est la relation entre les sommets.

Un arbre est un graphe qui vérifie les propriétés suivantes :

• Connexité : il est toujours possible d'aller d'un sommet à l'autre par un chemin d'arêtes. Dans le cas de la carte routière, cela revient à dire qu'il est toujours possible d'aller d'une ville à l'autre par la route.
• Acyclique : il est impossible de partir d'un sommet et d'y revenir sans rebrousser chemin à un moment.

Un graphe est un couple ${\displaystyle (S,A)}$ tel que

• ${\displaystyle S}$ est un ensemble non vide quelconque dont les éléments sont appelés sommets ou nœuds.
• ${\displaystyle A\subset \{\{x,y\}\,|\,x,y\in S,\,x\neq y\}}$. Les éléments de ${\displaystyle A}$ sont appelés les arêtes.

Un arbre est un graphe ${\displaystyle (S,A)}$ tel que

• (Connexité) ${\displaystyle \forall x,y\in S{\text{ tels que }}x\neq y,\,\exists x_{1},\dots ,x_{n}\in S{\text{ tels que }}\{x,x_{1}\},\{x_{1},x_{2}\},\dots ,\{x_{n},y\}\in A}$.
• (Acyclique) ${\displaystyle \forall x\in S,\,\nexists x_{1},\dots ,x_{n}\in S{\text{ tels que }}\{x,x_{1}\},\{x_{1},x_{2}\}\dots ,\{x_{n},x\}\in A}$.

Dans le cas d'arbres finis, c'est-à-dire quand l'ensemble des sommets est fini, il existe une définition alternative. En effet, il est possible de définir par récurrence l'ensemble des arbres finis dont les sommets appartiennent à un ensemble non vide donné E (fini ou infini) :

• si s est un élément de E alors ({s},∅) est un arbre ;
• si (S, A) est un arbre alors (S ∪ {x}, A ∪ { {x,s} }) est un arbre pour x quelconque dans E n'appartenant pas à S et s appartenant à S ;
• aucun autre graphe n'est un arbre.

Autrement dit, l'ensemble des arbres dont les sommets appartiennent à E est le plus petit ensemble de graphes qui vérifie les deux premières règles ci-dessus.

Il existe plusieurs notions très utiles associées aux arbres, certaines sont données dans le tableau ci-dessous. Les notions données ici sont en fait toutes valables dans le cadre général de graphes. Dans le tableau on se fixe un arbre (S,A).

Notion	Définition intuitive	Définition formelle
Sommets adjacents	Deux sommets x et y sont adjacents s'ils sont reliés par une arête.	${\displaystyle x,y\in S{\text{ tels que }}\{x,y\}\in A}$
Arêtes adjacentes	Deux arêtes a1 et a2 sont adjacentes si elles partagent une extrémité en commun.	${\displaystyle a_{1},a_{2}\in E{\text{ telles que }}\#a_{1}\cup a_{2}\leq 3}$
Degré d'un sommet x	Nombre de sommets adjacents à x.	${\displaystyle \deg(x)=\#\{y\in S\,|\,\{x,y\}\in A\}}$
Feuille	Sommet x dont le degré vaut 1.	${\displaystyle x\in S{\text{ tel que}}\deg(x)=1}$
Sommet interne	Sommet x dont le degré est strictement supérieur à 1.	${\displaystyle x\in S{\text{ tel que}}\deg(x)>1}$
Chemin d'arêtes	Chemin constitué de plusieurs arêtes adjacentes mises bout à bout.	${\displaystyle a_{1},\dots ,a_{n}\in E{\text{ telles que }}\forall i,a_{i}{\text{ adjacente à }}a_{i+1}}$
Distance entre deux sommets x et y	Taille du plus court chemin reliant x et y.	Si x et y sont distincts alors la distance d(x,y) vaut ${\displaystyle \min\{n\geq 1\,|\,\exists {\text{ chemin }}a_{1},\dots ,a_{n}\in A{\text{ tel que }}x\in a_{1}{\text{ et }}y\in a_{n}\}}$ et sinon la distance vaut 0.

Un arbre fini avec 4 feuilles (les sommets n^os 1, 3, 5, 7) et 3 sommets internes (les sommets n^os 2, 4 et 6).

Un arbre fini est un arbre tel que l'ensemble de ses sommets est fini. Formellement, un arbre (S,A) est fini si S est de cardinal fini.

On peut remarquer les propriétés suivantes :

• Un arbre fini est un graphe connexe dont le nombre de sommets excède le nombre d'arêtes d'une unité exactement. Autrement dit le graphe (S,A) est un arbre si et seulement s'il est connexe et |S| = |A|+1.

• Un arbre fini est un graphe sans cycles dont le nombre de sommets excède le nombre d'arêtes d'une unité exactement. Autrement dit le graphe (S,A) est un arbre si et seulement s'il est acyclique et |S| = |A|+1.

Dans le cas particulier où S est l'ensemble des entiers entre 1 et n alors on dit que l'arbre (S,A) est un arbre de Cayley (avec n sommets).

Un arbre localement fini est un arbre tel que le degré de chaque sommet est fini. Formellement, un arbre (S,A) est localement fini si pour tout sommet x de S, deg(x) est fini.

Un arbre fini est toujours localement fini mais la réciproque n'est pas vraie. Le nombre de sommets d'un arbre localement fini est fini ou dénombrable.

Démonstration

Soit ${\displaystyle T=(S,A)}$ un arbre localement fini. Fixons un élément quelconque ${\displaystyle r\in S}$. Pour tout ${\displaystyle n\in \mathbb {N} }$, notons ${\displaystyle D_{n}=\{x\in S\,|\,d(x,r)=n\}}$ l'ensemble des sommets à distance exactement ${\displaystyle n}$ de ${\displaystyle r}$. Par connexité de ${\displaystyle T}$ on peut voir que tous ses sommets appartiennent à l'un des ${\displaystyle D_{n}}$. Autrement dit

${\displaystyle S=\bigcup _{n\geq 0}D_{n}.}$

D'autre part on peut montrer par récurrence, en utilisant le fait que ${\displaystyle T}$ est localement fini, que pour tout ${\displaystyle n\geq 0,\,D_{n}}$ est fini. Ainsi ${\displaystyle S}$ est une union dénombrable d'ensembles finis donc est fini ou dénombrable.

Un arbre enraciné est simplement un arbre dont un sommet porte le statut particulier de racine. Formellement, un arbre enraciné est un triplet (S,A,r) où (S,A) est un arbre et r est un élément de S appelé racine.

Cette notion de racine permet de se munir d'un ordre de type ancêtre/descendant entre les sommets de l'arbre. Les arbres enracinés sont utiles pour modéliser la généalogie d'une population.

Notion	Définition intuitive	Définition formelle
Hauteur d'un sommet x	Distance entre x et la racine r.	${\displaystyle H(x)=d(x,r)}$
Enfant (ou fils) d'un sommet x	Sommet adjacent à x dont la hauteur vaut celle de x plus 1.	${\displaystyle y\in S{\text{ tel que }}\{x,y\}\in A{\text{ et }}H(y)=H(x)+1}$
Parent d'un sommet x	Sommet tel que x est son enfant.	${\displaystyle y\in S{\text{ tel que }}\{x,y\}\in A{\text{ et }}H(y)=H(x)-1}$
Descendant d'un sommet x[3]	Sommet qui découle d'une lignée parent/enfant partant de x.	${\displaystyle y\in S{\text{ tel que }}\exists \{x_{1},x_{2}\},\{x_{2},x_{3}\},\dots ,\{x_{n-1},x_{n}\}\in A}$ ${\displaystyle {\text{ tel que }}x_{1}=x,\,x_{n}=y{\text{ et }}\forall i,\,x_{i}{\text{ est le parent de }}x_{i+1}}$
Ancêtre d'un sommet x[3]	Sommet tel que x est un descendant.	${\displaystyle y\in S{\text{ tel que }}\exists \{x_{1},x_{2}\},\{x_{2},x_{3}\},\dots ,\{x_{n-1},x_{n}\}\in A}$ ${\displaystyle {\text{ tel que }}x_{1}=y,\,x_{n}=x{\text{ et }}\forall i,\,x_{i}{\text{ est le parent de }}x_{i+1}}$
Arête découlant d'un sommet x	Arête qui relie x à un de ses enfants.	${\displaystyle \{x,y\}\in A{\text{ tel que }}H(y)=H(x)+1}$

Un arbre étiqueté est un arbre dont les sommets (ou les arêtes) possèdent une étiquette, c'est-à-dire un élément d'un ensemble non vide quelconque (souvent les étiquettes sont des entiers ou des nombres réels).

Un arbre possède toujours un étiquetage de sommets canonique : chaque sommet reçoit lui-même en tant qu'étiquète. Ainsi un arbre de Cayley de n sommets peut être vu comme un arbre étiqueté de manière injective avec les entiers de 1 à n. Avec cet étiquetage canonique, les sommets ont tous des étiquettes différentes. L'avantage du concept d'étiquette est qu'il est possible de donner des étiquettes identiques à plusieurs sommets différents.

Un arbre orienté est un arbre où les arêtes sont orientées, c'est-à-dire qu'elles ont une direction (elles partent d'un sommet pour arriver à un autre). Formellement un arbre orienté est un couple ${\displaystyle (S,{\hat {A}})}$ tel que

• ${\displaystyle {\hat {A}}\subset \{(x,y)\,|\,x,y\in S,\,x\neq y\}}$.
• Si on note ${\displaystyle A=\{\{x,y\}\,|\,(x,y)\in {\hat {A}}\}}$ alors ${\displaystyle (S,A)}$ est un arbre.

Un arbre enraciné possède deux orientations canoniques :

• les arêtes sont orientées du descendant le plus éloigné de la racine vers le descendant le plus proche. Formellement, on prend ${\displaystyle {\hat {A}}=\{(x,y)\,|\,\{x,y\}\in A{\text{ et }}H(x)=H(y)+1\}}$.
• les arêtes sont orientées du descendant le plus proche de la racine vers le descendant le plus éloigné. Formellement, on prend ${\displaystyle {\hat {A}}=\{(x,y)\,|\,\{x,y\}\in A{\text{ et }}H(x)=H(y)-1\}}$.

Un arbre orienté est toujours connexe par définition (on dit aussi faiblement connexe) mais n'est pas forcément fortement connexe. En fait le seul arbre orienté fortement connexe est l'arbre trivial qui ne possède qu'un seul sommet.

Un arbre ordonné est un arbre enraciné tel que pour chaque sommet, un ordre total a été spécifié pour l'ensemble des enfants de ce sommet.

On peut démontrer qu'il y a n^{n – 2} arbres numérotés à n sommets. La découverte de cette formule a été attribuée un temps à Arthur Cayley. Pour cette raison, les arbres comme graphes sont parfois appelés arbres de Cayley. Parmi de nombreuses démonstrations, citons celle qui utilise la bijection de Joyal : pour compter les éléments de l'ensemble ${\displaystyle \ {\mathcal {C}}_{n}\ }$ des arbres de Cayley à n sommets, Joyal établit une bijection entre ${\displaystyle \ {\mathcal {C}}_{n}\times [\![1,n]\!]^{2}\ }$ et l'ensemble des applications de ${\displaystyle \ [\![1,n]\!]\ }$ dans ${\displaystyle \ [\![1,n]\!]\ }$, noté usuellement ${\displaystyle \ [\![1,n]\!]^{[\![1,n]\!]}\ }$. On a ainsi

${\displaystyle n^{n}\ =\ {\text{Card}}\ \left([\![1,n]\!]^{[\![1,n]\!]}\right)\ =\ {\text{Card}}\ \left({\mathcal {C}}_{n}\times [\![1,n]\!]^{2}\right)\ =\ n^{2}\,{\text{Card}}\ {\mathcal {C}}_{n}.}$

Si on choisit un sommet r quelconque dans un arbre, il est possible d'enraciner l'arbre en r, c'est-à-dire orienter toutes les arêtes de sorte qu'il existe un chemin de r à tous les autres nœuds. On obtient alors un arbre enraciné.

Un arbre est un graphe planaire : un graphe qu'on peut dessiner dans le plan sans que ses arêtes ne se touchent, sauf à leurs extrémités. Un tel dessin est parfois appelé plongement d'un graphe. La plupart des graphes planaires ont plusieurs plongements non homéomorphes, au sens où, pour au moins deux de ces plongements, il n'existe pas d'homéomorphisme du plan entier vers lui-même qui envoie un plongement sur l'autre plongement[4] : les classes d'homéomorphismes de ces plongements sont appelés cartes planaires. Les classes d'homéomorphismes des plongements des arbres (graphes) sont aussi appelés arbres (planaires, généraux, de Catalan). Pour le dénombrement, il est commode de les munir d'une racine, à savoir une arête orientée : on parle alors d'arbres planaires enracinés. Ainsi le nombre d'arbres planaires enracinés à n arêtes est le n-ième nombre de Catalan :

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{n!(n+1)!}}.}$

Les 5 arbres planaires à 3 arêtes, en haut, et les 16 arbres de Cayley à 3 arêtes, en bas. L'arête racine des arbres planaires va du point rouge au point bleu.

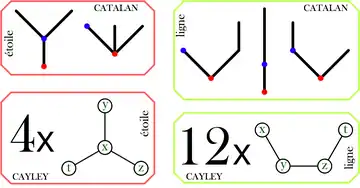
Les arbres planaires sont non étiquetés, alors que les arbres de Cayley le sont (les n sommets sont étiquetés de 1 à n). Par exemple, il y a deux arbres non enracinés et non étiquetés à 3 arêtes, celui qui possède un sommet de degré 3 et 3 feuilles (étoile à 3 branches) et celui qui possède 2 sommets de degré 2 et deux feuilles (ligne).

• L'étoile peut être étiquetée de 4 manières (en choisissant librement l'étiquette du centre, parmi 4 possibilités, le choix des étiquettes des 3 feuilles conduisant alors toujours au même arbre). La ligne peut être étiquetée de 4!=24 manières, équivalentes 2 par 2 (par exemple 1234 et 4321 sont équivalents), donc de 12 manières en réalité, ce qui donne 12 + 4 = 16 = 4² arbres de Cayley à 3 arêtes.
• L'étoile peut être enracinée de deux manières : la racine peut être une des trois arêtes, peu importe laquelle, les deux choix non homéomorphes sont les choix d'une arête rentrante (vers le centre) ou sortante. La ligne peut être enracinée de 3 manières, extrémité sortante ou rentrante, ou arête centrale, d'où 5 arbres planaires :

${\displaystyle 2+3=5=C_{3}={\frac {1}{4}}{6 \choose 3}={\frac {6!}{3!4!}}.}$

L'arbre peut être représenté avec l'origine de l'arête racine en bas ou en haut (en informatique, la racine est souvent figurée en haut), et l'arête racine soit complètement à droite soit complètement à gauche (dans la figure ci-dessus l'arête racine commence au point rouge et aboutit au point bleu).

Notation de Neveu pour les sommets d'un arbre planaire.

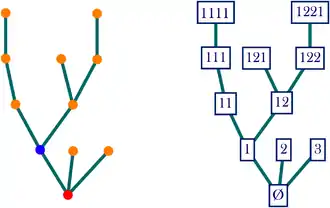
Un arbre planaire enraciné peut être décrit de manière non ambigüe par la liste de ses sommets, chacun désigné par une suite finie d'entiers, qui sont les positions, au sein de leur fratrie, des ancêtres du sommet : c'est la notation de Neveu[5]. On utilise ici l'arbre généalogique comme métaphore pour l'arbre planaire : le sommet 2|4|3 désigne le 3^e fils du 4^e fils du 2^e fils de l'ancêtre (l'ancêtre étant lui-même désigné par la suite vide, notée ${\displaystyle \scriptstyle \emptyset \ }$). Par convention, l'ancêtre est le sommet initial de l'arête racine, et le sommet final de l'arête racine est le fils ainé de l'ancêtre : en tant que tel, il est noté 1. La longueur de la suite associée à un sommet est la hauteur (ou la profondeur) du sommet, i.e. la distance entre ce sommet et le début de la racine, qui représente l'ancêtre : en filant la métaphore, un sommet de hauteur n représente un individu appartenant à la n-ème génération de la population fondée par l'ancêtre.

Notation de Neveu: 5 arbres à 3 arêtes.

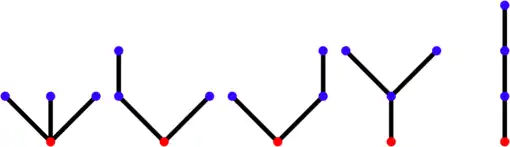
Les 5 arbres à 3 arêtes sont ainsi décrits par les 5 ensembles de mots

${\displaystyle \{\emptyset ,1,2,3\},~\{\emptyset ,1,11,2\},~\{\emptyset ,1,2,21\},~\{\emptyset ,1,11,12\}~{\text{et}}~\{\emptyset ,1,11,111\}.}$

Le parcours des sommets dans l'ordre lexicographique est alors le parcours en profondeur préfixé (ou parcours préfixe) d'un arbre vu comme structure de données en informatique. Par ailleurs, à travers la notation de Neveu, on perçoit comment un arbre planaire encode commodément une réalisation de processus de Galton-Watson avec extinction : l'arbre aléatoire obtenu en encodant une réalisation de processus de Galton-Watson est parfois appelé arbre de Galton-Watson. Rien ne s'oppose à définir un arbre planaire infini à l'aide de la notation de Neveu, ce qui permet d'encoder les réalisations de processus de Galton-Watson où la population ne s'éteint pas.

• Arbre (mathématiques)
• Preuve combinatoire : différence entre preuve par bijection et preuve par double dénombrement
• Terme (logique)
• Lexique de la théorie des graphes
• Arbre enraciné
• Polyarbre
• Pseudo-forêt

• (en) Martin Aigner et Günter M. Ziegler, Proofs from THE BOOK, Berlin, Springer, 2003, 3^e éd., 240 p. (ISBN 978-3-540-40460-6, BNF 39082186), p. 141-146
• Philippe Flajolet et Robert Sedgewick, An Introduction to the Analysis of Algorithms, Addison-Wesley, 1995 (ISBN 978-0-201-40009-0)