Preuve par double dénombrement

Soient deux ensembles finis ${\displaystyle {\mathcal {E}}}$ et ${\displaystyle {\mathcal {F}}}$, et une partie ${\displaystyle {\mathcal {G}}}$ de ${\displaystyle {\mathcal {E}}\times {\mathcal {F}}}$ ; chaque fois que ${\displaystyle (x,y)}$ appartient à ${\displaystyle {\mathcal {G}}}$, on dit que ${\displaystyle x}$ et ${\displaystyle y}$ sont incidents.

Notons que ${\displaystyle {\mathcal {G}}}$ peut être vu comme le graphe d'une relation binaire ${\displaystyle R}$ de ${\displaystyle {\mathcal {E}}}$ vers ${\displaystyle {\mathcal {F}}}$, auquel cas "${\displaystyle x}$ et ${\displaystyle y}$ incidents" s'écrit ${\displaystyle xRy}$, ou encore comme un graphe biparti.

Si ${\displaystyle n^{+}(x)}$ désigne le nombre d'éléments ${\displaystyle y}$ incidents à ${\displaystyle x}$, et ${\displaystyle n^{-}(y)}$ celui des éléments ${\displaystyle x}$ incidents à ${\displaystyle y}$, on a alors la formule dite du double décompte, ou du comptage par tranches (ou par piles) [2]:

${\displaystyle \sum _{x\in E}n^{+}(x)=\sum _{y\in F}n^{-}(y)=\left\vert {\mathcal {G}}\right\vert ={\text{card }}{\mathcal {G}}}$.

Un cas particulier intéressant est celui où ${\displaystyle n^{+}}$ et ${\displaystyle n^{-}}$ sont constants ; la formule s'écrit alors ${\displaystyle n^{+}.\left\vert {\mathcal {E}}\right\vert =n^{-}.\left\vert {\mathcal {F}}\right\vert }$.

La formule du double décompte s'écrit dans cet exemple : ${\displaystyle 1+2+2+1+2=3+2+1+2=8}$

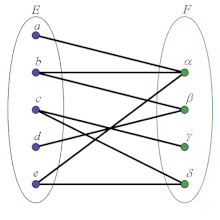
La formule du double décompte s'interprète dans ce diagramme par le fait que le nombre de flèches est égal au nombre de leurs départs ainsi qu'au nombre de leurs arrivées.

Si on définit la matrice d'incidence ${\displaystyle A}$ du graphe ${\displaystyle {\mathcal {G}}}$ ou de la relation ${\displaystyle R}$ par ${\displaystyle A(x,y)=1}$ si ${\displaystyle (x,y)}$ appartient à ${\displaystyle {\mathcal {G}}}$, ${\displaystyle A(x,y)=0}$ sinon, la formule du double décompte signifie que la somme des termes de la matrice ${\displaystyle A}$ s'obtient soit en sommant lignes par lignes, soit en sommant colonnes par colonnes. En effet ${\displaystyle n^{+}(x)}$ est le nombre de ${\displaystyle 1}$ situés dans la ligne associée à ${\displaystyle x}$, et ${\displaystyle n^{-}(y)}$ est le nombre de ${\displaystyle 1}$ situés dans la colonne associée à ${\displaystyle y}$.

Dans l'exemple ci-contre, la matrice d'incidence est ${\displaystyle A={\begin{pmatrix}&\alpha &\beta &\gamma &\delta \\a&1&0&0&0\\b&1&1&0&0\\c&0&0&1&1\\d&0&1&0&0\\e&1&0&0&1\end{pmatrix}}}$.

En ce sens, la formule du double décompte est un cas particulier de la formule d'interversion de signes de sommation : ${\displaystyle \sum _{(i,j)\in I\times J}a_{i,j}=\sum _{i\in I}\sum _{j\in J}a_{i,j}=\sum _{j\in J}\sum _{i\in I}a_{i,j}}$.

Ici, les ensembles ${\displaystyle {\mathcal {E}}}$ et ${\displaystyle {\mathcal {F}}}$ sont égaux à l'ensemble des entiers de 1 à ${\displaystyle n}$, et deux entiers ${\displaystyle i}$ et ${\displaystyle j}$ sont incidents si ${\displaystyle i\leqslant j}$ .

Alors ${\displaystyle n^{+}(i)=n+1-i}$ et ${\displaystyle n^{-}(i)=i}$

La formule du double décompte s'écrit alors ${\displaystyle \sum _{i=1}^{n}(n+1-i)=\sum _{i=1}^{n}i}$, dont on déduit la formule classique ${\displaystyle \sum _{i=1}^{n}i={n(n+1) \over {2}}}$.

Courbe du nombre moyen de diviseurs d'un nombre entre 1 et ${\displaystyle n}$ avec, en rouge, la courbe de ${\displaystyle \ln n}$.

Mêmes ensembles ${\displaystyle {\mathcal {E}}}$ et ${\displaystyle {\mathcal {F}}}$ , mais ${\displaystyle i}$ et ${\displaystyle j}$ sont incidents si ${\displaystyle i}$ divise ${\displaystyle j}$.

Alors ${\displaystyle n^{+}(i)}$ est le nombre de multiples de ${\displaystyle i}$ inférieurs ou égaux à ${\displaystyle n}$, qui vaut ${\displaystyle \left\lfloor {\frac {n}{i}}\right\rfloor }$ où ${\displaystyle \left\lfloor .\right\rfloor }$ désigne la partie entière, et ${\displaystyle n^{-}(i)}$ est le nombre ${\displaystyle d(i)}$ des diviseurs de ${\displaystyle i}$.

La formule du double décompte s'écrit alors ${\displaystyle \sum _{i=1}^{n}d(i)=\sum _{i=1}^{n}\left\lfloor {\frac {n}{i}}\right\rfloor }$ ; on en déduit facilement que ${\displaystyle {1 \over n}\sum _{i=1}^{n}d(i)\sim \sum _{i=1}^{n}{1 \over i}=H_{n}}$ (série harmonique), et comme ${\displaystyle H_{n}\sim \ln n}$, on obtient que le nombre moyen de diviseurs d'un nombre entre 1 et ${\displaystyle n}$ équivaut à ${\displaystyle \ln n}$.

Ici, l'ensemble ${\displaystyle {\mathcal {E}}}$ est l'ensemble des sommets d'un graphe, ${\displaystyle {\mathcal {F}}}$ l'ensemble de ses arêtes, et la relation d'incidence celle d'adjacence entre les sommets et les arêtes. Pour un sommet ${\displaystyle s}$, ${\displaystyle n^{+}(s)}$ s'interprète comme le degré de ${\displaystyle s}$, et pour une arête ${\displaystyle a}$, ${\displaystyle n^{-}(a)=2}$ ; la formule du double décompte s'écrit alors ${\displaystyle \sum \operatorname {deg} (s)=2A}$ où ${\displaystyle A}$ est le nombre d'arêtes du graphe. On en déduit que le nombre de sommets de degré impair est pair, ce qui constitue le lemme des poignées de main.

On en déduit aussi par exemple que dans un polyèdre dont tous les sommets sont de degré ${\displaystyle n}$, ${\displaystyle nS=2A}$ où ${\displaystyle S}$ est le nombre de sommets.

De la même façon, dans un polyèdre où toutes les faces ont ${\displaystyle p}$ arêtes, ${\displaystyle pF=2A}$ où ${\displaystyle F}$ est le nombre de faces.

Ici, l'ensemble ${\displaystyle {\mathcal {E}}}$ est l'ensemble des parties à ${\displaystyle p}$ éléments d'un ensemble à ${\displaystyle n}$ éléments et ${\displaystyle {\mathcal {F}}}$ l'ensemble des parties à ${\displaystyle q}$ éléments ; on décrète que deux parties ${\displaystyle A}$ et ${\displaystyle B}$ sont incidentes si elles sont disjointes.

Le nombre d'éléments du graphe ${\displaystyle {\mathcal {G}}}$ vaut ${\displaystyle {\binom {n}{p+q}}{\binom {p+q}{p}}}$ (choix de ${\displaystyle A\cup B}$, puis choix de ${\displaystyle A}$ dans ${\displaystyle A\cup B}$). Or ici ${\displaystyle n^{+}(A)}$, qui est le nombre de ${\displaystyle B}$ disjoints de ${\displaystyle A}$, vaut ${\displaystyle {\binom {n-p}{q}}}$, et ${\displaystyle n^{-}(B)}$ vaut ${\displaystyle {\binom {n-q}{p}}}$. La formule du double décompte s'écrit alors :

${\displaystyle {\binom {n}{p}}{\binom {n-p}{q}}={\binom {n}{q}}{\binom {n-q}{p}}={\binom {n}{p+q}}{\binom {p+q}{p}}}$.

Par exemple, en faisant ${\displaystyle q=1}$, on obtient ${\displaystyle (n-p){\binom {n}{p}}=n{\binom {n-1}{p}}=(p+1){\binom {n}{p+1}}}$, ce qui, en changeant ${\displaystyle p}$ en ${\displaystyle p-1}$ donne l'importante formule du pion :

${\displaystyle {\binom {n}{p}}={n \over p}{\binom {n-1}{p-1}}}$.

Cherchons le nombre de parties d'un ensemble à n éléments.

Première méthode : il y a deux possibilités pour chaque élément : soit il est dans la partie, soit il n'y est pas. Par conséquent, il y a un total de ${\displaystyle 2\times 2\times \ldots \times 2\,(n{\mbox{ fois}})=2^{n}}$ parties.

Deuxième méthode : le nombre d'éléments dans une partie est un entier ${\displaystyle p}$ entre 0 et ${\displaystyle n}$. Le nombre de parties à ${\displaystyle p}$ éléments est le coefficient binomial ${\displaystyle {\binom {n}{p}}}$, Ainsi, le nombre de parties est ${\displaystyle \sum _{p=0}^{n}{\binom {n}{p}}}$.

L'égalisation des deux expressions donne :

${\displaystyle \sum _{p=0}^{n}{\binom {n}{p}}=2^{n}}$

Collier représentant 7 mots différents.

Le petit théorème de Fermat affirme que « si ${\displaystyle p}$ est un nombre premier et si ${\displaystyle a}$ est un entier quelconque, alors ${\displaystyle a^{p}-a}$ est un multiple de ${\displaystyle p}$ ». Par exemple :

4³ - 4 = 60 qui est divisible par 3.

Soit ${\displaystyle p}$ un nombre premier et ${\displaystyle a}$ un nombre entier. Considérons un alphabet constitué de ${\displaystyle a}$ symboles. Comptons les ${\displaystyle n}$ mots de longueur ${\displaystyle p}$ dans lesquels il y a au moins deux symboles distincts.

Première méthode : il y a en tout ${\displaystyle a^{p}}$ mots de longueur ${\displaystyle p}$ dans l'alphabet, desquels il faut retirer les ${\displaystyle a}$ mots constitués d'un seul et même symbole :

${\displaystyle n=a^{p}-a}$

Collier ne représentant qu'un seul mot.

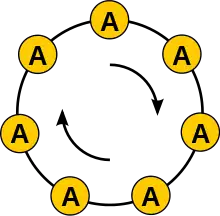
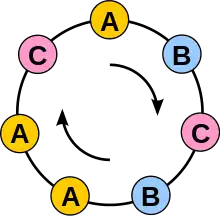
Deuxième méthode : ces mots peuvent être regroupés en ensembles de mots qui peuvent être déduits l'un de l'autre par permutation circulaire. On appelle ces ensembles des colliers (illustration). Par exemple, si l'alphabet est ${\displaystyle \{A,B,C,D\}}$ et si l'on considère des mots de trois lettres, les trois mots ${\displaystyle ABD}$, ${\displaystyle BDA}$ et ${\displaystyle DAB}$ sont dans le même collier.

Il y a ${\displaystyle p}$ mots de ${\displaystyle p}$ symboles dans chaque collier. En effet, chacune des ${\displaystyle p}$ permutations donne un mot différent, car ${\displaystyle p}$ est premier. Ce ne serait pas le cas si ${\displaystyle p}$ n'était pas premier, il n'y a par exemple que 2 mots différents de 4 symboles dans le collier ${\displaystyle ABAB}$. On a donc :

${\displaystyle n=p.{\text{(nombre de colliers)}}}$

En écrivant l'égalité entre ces deux expressions pour ${\displaystyle n}$, on trouve que ${\displaystyle n=a^{p}-a}$ est divisible par ${\displaystyle p}$.

La formule de Cayley indique qu'il y a 1 = 2^{2 − 2} arbre à deux sommets, 3 = 3^{3 − 2} arbres colorés à trois sommets et 16 = 4^{4 − 2} arbres colorés à 4 sommets.

Quel est le nombre ${\displaystyle C_{n}}$ d'arbres colorés différents qui peuvent recouvrir un ensemble de ${\displaystyle n}$ sommets distincts ? La formule de Cayley donne la réponse :

${\displaystyle C_{n}=n^{n-2}}$.

Aigner et Ziegler énumèrent quatre démonstrations différentes de ce résultat. Ils affirment que, des quatre, c'est la démonstration par double dénombrement que l'on doit à Jim Pitman qui est « la plus belle d'entre elles »[4] - [5].

Dans cette démonstration on dénombre de deux façons les différentes suites d'arêtes orientées qui peuvent être ajoutées à un graphe nul (sans arêtes) de n sommets pour former un arbre.

Première méthode : on part de l'un des ${\displaystyle C_{n}}$ arbres non orientés possibles et on choisit l'un de ses n sommets comme racine de l'arbre orienté, ce qui donne un arbre orienté. Il y a ${\displaystyle n-1}$ façons de choisir la première arête, puis ${\displaystyle n-2}$ façons de choisir l'arête suivante, et ainsi de suite. Finalement, le nombre total de suites qui peuvent être formées de cette façon est :

${\displaystyle C_{n}n!}$.

Ajouter une arête orientée à une forêt orientée.

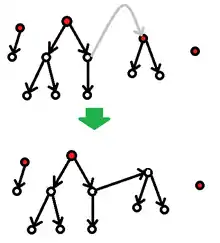
Deuxième méthode : on ajoute les arêtes une à une au graphe vide, en considérant le nombre de choix que l'on a à disposition à chaque étape. Si l'on a déjà ajouté une collection de ${\displaystyle n-k}$ arêtes de façon à former une forêt de k arbres orientés (illustration), il y a ${\displaystyle n(k-1)}$ choix pour la prochaine arête à ajouter. En effet, son sommet de départ peut être n'importe lequel des n sommets du graphe et son sommet d'arrivée peut être n'importe lequel des ${\displaystyle k-1}$ racines autres que la racine de l'arbre contenant le sommet de départ (illustration). Finalement, en multipliant le nombre de choix à la première étape, à la deuxième étape, etc., le nombre total de choix est :

${\displaystyle \prod _{k=2}^{n}n(k-1)=n^{n-1}(n-1)!=n^{n-2}n!}$.

En écrivant l'égalité entre ces deux expressions pour le nombre de suites d'arêtes,

${\displaystyle C_{n}n!=n^{n-2}n!}$,

on obtient la formule de Cayley :

${\displaystyle C_{n}=n^{n-2}}$.

• L'identité de Vandermonde, l'identité de l'étoile de David, autres propriétés des coefficients binomiaux qui peuvent être démontrées par double dénombrement.
• Les nombres pyramidaux carrés. L'égalité entre la somme des n premiers carrés et un polynôme du troisième degré peut être démontrée par double dénombrement des triplets de nombres entiers (x, y, z) où z est plus grand que chacun des deux autres nombres.
• L'Inégalité de Lubell-Yamamoto-Meshalkin. La démonstration de D. Lubell de ce résultat sur les familles d'ensembles utilise un argument de double dénombrement sur des permutations pour prouver cette fois une inégalité plutôt qu'une égalité.
• La loi de réciprocité quadratique. Une démonstration due à Gotthold Eisenstein permet d'obtenir cet autre résultat important de la théorie des nombres, en comptant de deux façons différentes les points d'un réseau dans un triangle.