Lemme des poignées de main
En théorie des graphes, une branche des mathématiques, le lemme des poignées de main est la déclaration selon laquelle chaque graphe non orienté fini a un nombre pair de sommets de degré impair. Plus trivialement, dans une réunion de plusieurs personnes dont certaines se serrent la main, un nombre pair de personnes devra serrer un nombre impair de fois la main d'autres personnes.
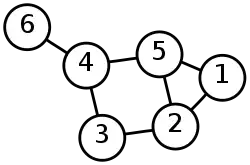
Description
Le lemme des poignées de main est une conséquence de la formule de la somme des degrés (qu'on qualifie quelquefois de lemme des poignées de main),
pour un graphe ayant un ensemble de sommets V[N 1] et un ensemble d'arêtes E[N 2]. Ce résultat a été prouvé par Leonhard Euler dans son célèbre article de 1736 sur le Problème des sept ponts de Königsberg, texte fondateur de l'étude de la théorie des graphes.
Dans un graphe, on appelle parfois les sommets de degré impair des nœuds impairs ou sommets impairs ; sous cette terminologie, le lemme des poignées de main peut être reformulé ainsi : chaque graphe fini possède un nombre pair de nœuds impairs.
Démonstration
La démonstration de la formule de la somme des degrés constitue un exemple de preuve par double dénombrement : on compte de deux façons différentes le nombre des extrémités des arêtes :
- c'est le double du nombre d'arêtes, chaque arête ayant deux extrémités ;
- c'est aussi la somme des degrés de chaque sommet.
Le nombre d'extrémités des arêtes étant pair d'après le premier point, on en déduit que les contributions impaires dans la somme du deuxième point sont en nombre pair, d'où le résultat.
Graphes infinis

Le lemme des poignées de main ne s'applique pas aux graphes infinis, même quand ils ont un nombre fini de sommets de degré impair. Par exemple, un graphe chaîne infini à une seule extrémité (figure) comporte exactement un sommet de degré impair (celui du bout), or 1 est un nombre impair.
Cas des graphes réguliers

La formule sur la somme des degrés implique que tout graphe régulier de degré à sommets possède arêtes[1]. Une conséquence est que si le degré est impair, alors le nombre d'arêtes est divisible par .
Notes
- V pour vertex qui signifie « sommet » en anglais.
- E pour edge qui signifie « arête » en anglais.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Handshaking lemma » (voir la liste des auteurs).
- (en) Joan M. Aldous et Robin J. Wilson, Graphs and Applications : an Introductory Approach, Springer-Verlag, , 444 p. (ISBN 978-1-85233-259-4, lire en ligne), « Theorem 2.2 », p. 44.



